Днес ще говорим за логаритмични формулии направете демонстрация примери за решение.

Сами по себе си те предполагат модели на решение според основните свойства на логаритмите. Преди да приложим формулите за логаритъм към решението, ние ви припомняме първо всички свойства:

Сега, въз основа на тези формули (свойства), показваме примери за решаване на логаритми.

Примери за решаване на логаритми по формули.

Логаритъмположително число b при основа a (означено като log a b) е степента, до която a трябва да се повдигне, за да се получи b, с b > 0, a > 0 и 1.

Според определението log a b = x, което е еквивалентно на a x = b, така че log a a x = x.

Логаритми, примери:

log 2 8 = 3, защото 2 3 = 8

log 7 49 = 2 защото 7 2 = 49

log 5 1/5 = -1, защото 5 -1 = 1/5

Десетичен логаритъме обикновен логаритъм, чиято основа е 10. Означава се като lg.

log 10 100 = 2 защото 10 2 = 100

натурален логаритъм- също обичайният логаритъм логаритъм, но с основата e (e \u003d 2.71828 ... - ирационално число). Наричан като ln.

Желателно е да си припомним формулите или свойствата на логаритмите, защото те ще ни трябват по-късно при решаване на логаритми, логаритмични уравнения и неравенства. Нека да разгледаме всяка формула отново с примери.

• Основно логаритмично тъждество
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Логаритъмът на произведението е равен на сбора от логаритмите
  log a (bc) = log a b + log a c

  log 3 8.1 + log 3 10 = log 3 (8.1*10) = log 3 81 = 4

• Логаритъмът на частното е равен на разликата на логаритмите
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Свойства на степента на логаритмуемо число и основата на логаритъма

  Показателят на числото логаритъм log a b m = mlog a b

  Показател на основата на логаритъма log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  ако m = n, получаваме log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Преход към нова основа
  log a b = log c b / log c a,

  ако c = b, получаваме log b b = 1

  тогава log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Както можете да видите, формулите за логаритъм не са толкова сложни, колкото изглеждат. Сега, след като разгледахме примери за решаване на логаритми, можем да преминем към логаритмични уравнения. Ще разгледаме примери за решаване на логаритмични уравнения по-подробно в статията: "". Не пропускайте!

Ако все още имате въпроси относно решението, напишете ги в коментарите към статията.

Забележка: реших да получа образование в друг клас в чужбина като опция.

(от гръцки λόγος - "дума", "отношение" и ἀριθμός - "число") числа bпо разум а(log α b) се нарича такова число ° С, И b= a c, тоест log α b=° СИ b=a° Сса еквивалентни. Логаритъмът има смисъл, ако a > 0, a ≠ 1, b > 0.

С други думи логаритъмчисла bпо разум Аформулиран като показател, до който трябва да се повдигне число аза да получите номера b(логаритъмът съществува само за положителни числа).

От тази формулировка следва, че изчислението x= log α b, е еквивалентно на решаването на уравнението a x =b.

Например:

log 2 8 = 3, защото 8=2 3 .

Отбелязваме, че посочената формулировка на логаритъма дава възможност за незабавно определяне логаритмична стойносткогато числото под знака на логаритъма е определена степен на основата. Наистина, формулировката на логаритъма позволява да се обоснове, че ако b=a c, след това логаритъма на числото bпо разум аравно на с. Също така е ясно, че темата за логаритъм е тясно свързана с темата степен на числото.

Посочено е изчисляването на логаритъма логаритъм. Логаритъмът е математическа операция за вземане на логаритъм. Когато се взема логаритъм, продуктите от фактори се трансформират в суми от членове.

Потенциранее математическата операция, обратна на логаритъма. При потенциране дадената основа се повдига на степен на израза, върху който се извършва потенцирането. В този случай сумите на членовете се трансформират в произведението на факторите.

Доста често се използват реални логаритми с основа 2 (двоичен), e число на Ойлер e ≈ 2,718 (натурален логаритъм) и 10 (десетичен).

На този етап си струва да се обмисли проби от логаритмидневник 7 2 , вътре √ 5, lg0,0001.

И записите lg (-3), log -3 3.2, log -1 -4.3 нямат смисъл, тъй като в първия от тях отрицателно число се поставя под знака на логаритъма, във второто - отрицателно число в основата, а в третата - и отрицателно число под знака на логаритъма и единица в основата.

Условия за определяне на логаритъма.

Струва си да разгледаме отделно условията a > 0, a ≠ 1, b > 0. определение на логаритъм.Нека помислим защо са взети тези ограничения. Това ще ни помогне с равенство от формата x = log α b, наречено основно логаритмично тъждество, което пряко следва от дефиницията на логаритъма, дадена по-горе.

Вземете условието a≠1. Тъй като едно е равно на едно на произволна степен, тогава равенството x=log α bможе да съществува само когато b=1, но log 1 1 ще бъде всяко реално число. За да премахнем тази неяснота, ние приемаме a≠1.

Нека докажем необходимостта от условието а>0. При а=0според формулировката на логаритъма, може да съществува само когато b=0. И след това съответно дневник 0 0може да бъде всяко ненулево реално число, тъй като нула на всяка ненулева степен е нула. За да се премахне тази неяснота, условието a≠0. И когато а<0 би трябвало да отхвърлим анализа на рационалните и ирационалните стойности на логаритъма, тъй като показателят с рационален и ирационален показател се определя само за неотрицателни основи. Именно поради тази причина условието а>0.

И последното условие b>0следва от неравенството а>0, тъй като x=log α b, и стойността на степента с положителна основа авинаги позитивен.

Характеристики на логаритмите.

Логаритмихарактеризиращ се с отличителен Характеристика, което доведе до широкото им използване за значително улесняване на старателните изчисления. При прехода "към света на логаритмите" умножението се трансформира в много по-лесно събиране, делението в изваждане, а издигането на степен и вземането на корен се трансформират съответно в умножение и деление на степен.

Формулировката на логаритми и таблица с техните стойности (за тригонометрични функции) е публикувана за първи път през 1614 г. от шотландския математик Джон Напиер. Логаритмичните таблици, уголемени и детайлизирани от други учени, бяха широко използвани в научни и инженерни изчисления и останаха актуални, докато не започнаха да се използват електронни калкулатори и компютри.

Във връзка с

може да се постави задачата за намиране на което и да е от трите числа от другите две, дадени. Дадено е a и след това N се намира чрез степенуване. Ако са дадени N и тогава a се намира чрез извличане на корена на степен x (или степенуване). Сега разгледайте случая, когато при дадени a и N се изисква да се намери x.

Нека числото N е положително: числото a е положително и не е равно на единица: .

Определение. Логаритъмът на числото N при основа a е степента, на която трябва да повдигнете a, за да получите числото N; логаритъма се обозначава с

По този начин, в равенство (26.1), степента се намира като логаритъм от N при основа a. Вписвания

имат същото значение. Равенството (26.1) понякога се нарича основното тъждество на теорията на логаритмите; всъщност той изразява дефиницията на понятието логаритъм. По тази дефиниция основата на логаритъма a винаги е положителна и различна от единица; логаритмируемото число N е положително. Отрицателните числа и нулата нямат логаритми. Може да се докаже, че всяко число с дадена основа има точно определен логаритъм. Следователно равенството включва . Имайте предвид, че условието е съществено тук, в противен случай заключението не би било оправдано, тъй като равенството е вярно за всякакви стойности на x и y.

Пример 1. Намерете

Решение. За да получите числото, трябва да повдигнете основа 2 на степен Следователно.

Можете да записвате при решаване на такива примери в следната форма:

Пример 2. Намерете .

Решение. Ние имаме

В примери 1 и 2 лесно намерихме желания логаритъм, като представихме логаритмуемото число като степен на основа с рационален показател. В общия случай, например за и т.н., това не може да се направи, тъй като логаритъма има ирационална стойност. Нека обърнем внимание на един въпрос, свързан с това твърдение. В § 12 дадохме концепцията за възможността за определяне на всяка реална степен на дадено положително число. Това беше необходимо за въвеждането на логаритми, които по принцип могат да бъдат ирационални числа.

Помислете за някои свойства на логаритмите.

Свойство 1. Ако числото и основата са равни, то логаритъма е равен на едно и, обратно, ако логаритъма е равен на едно, то числото и основата са равни.

Доказателство. Нека По дефиницията на логаритъма имаме и откъде

Обратно, нека Тогава по дефиниция

Свойство 2. Логаритъмът от единица при всяка основа е равен на нула.

Доказателство. По дефиницията на логаритъма (нулевата степен на всяка положителна основа е равна на единица, виж (10.1)). Оттук

Q.E.D.

Обратното твърдение също е вярно: ако , тогава N = 1. Наистина имаме .

Преди да заявим следното свойство на логаритмите, нека се съгласим да кажем, че две числа a и b лежат от една и съща страна на трето число c, ако и двете са по-големи от c или по-малки от c. Ако едно от тези числа е по-голямо от c, а другото е по-малко от c, тогава казваме, че те лежат на противоположните страни на c.

Свойство 3. Ако числото и основата лежат от една и съща страна на единица, тогава логаритъма е положителен; ако числото и основата лежат на противоположните страни на единица, тогава логаритъма е отрицателен.

Доказателството за свойство 3 се основава на факта, че степента на a е по-голяма от едно, ако основата е по-голяма от едно и показателят е положителен, или основата е по-малък от едно и показателят е отрицателен. Степента е по-малка от единица, ако основата е по-голяма от единица и степента е отрицателна, или основата е по-малка от единица и степента е положителна.

Има четири случая, които трябва да бъдат разгледани:

Ние се ограничаваме до анализа на първия от тях, читателят ще разгледа останалите сам.

Нека тогава показателят в равенството не е нито отрицателен, нито равен на нула, следователно е положителен, т.е., което трябваше да се докаже.

Пример 3. Разберете кои от следните логаритми са положителни и кои са отрицателни:

Решение, а) тъй като числото 15 и основата 12 са разположени от една и съща страна на единицата;

б) , тъй като 1000 и 2 са разположени от една и съща страна на единицата; в същото време не е от съществено значение основата да е по-голяма от логаритмичното число;

в), тъй като 3.1 и 0.8 лежат на противоположните страни на единицата;

G) ; Защо?

д) ; Защо?

Следните свойства 4-6 често се наричат ​​​​правила на логаритъма: те позволяват, знаейки логаритмите на някои числа, да намерите логаритмите на техния продукт, коефициент, степен на всяко от тях.

Свойство 4 (правилото за логаритъм на произведението). Логаритъмът от произведението на няколко положителни числа в дадена основа е равен на сумата от логаритмите на тези числа в същата основа.

Доказателство. Нека са дадени положителни числа.

За логаритъма на тяхното произведение записваме равенството (26.1), определящо логаритъма:

От тук намираме

Сравнявайки показателите на първия и последния израз, получаваме необходимото равенство:

Имайте предвид, че условието е съществено; логаритъма от произведението на две отрицателни числа има смисъл, но в този случай получаваме

Като цяло, ако произведението на няколко фактора е положително, тогава неговият логаритъм е равен на сумата от логаритмите на модулите на тези фактори.

Свойство 5 (правило за частен логаритъм). Логаритъмът на частно от положителни числа е равен на разликата между логаритмите на делителя и делителя, взети при една и съща основа. Доказателство. Постоянно намирайте

Q.E.D.

Свойство 6 (правило за логаритъм на степен). Логаритъмът на степента на всяко положително число е равен на логаритъма от това число, умножен по експонентата.

Доказателство. Записваме отново основната идентичност (26.1) за числото:

Q.E.D.

Последица. Логаритъмът от корена на положително число е равен на логаритъма от корена на числото, разделен на степента на корена:

Можем да докажем валидността на това следствие, като представим как и използваме свойство 6.

Пример 4. Логаритъм по основа a:

а) (приема се, че всички стойности b, c, d, e са положителни);

б) (приема се, че ).

Решение, а) Удобно е този израз да се прехвърли на дробни степени:

Въз основа на равенства (26.5)-(26.7) сега можем да запишем:

Забелязваме, че върху логаритмите на числата се извършват по-прости операции, отколкото върху самите числа: при умножаване на числа техните логаритми се събират, при деление се изваждат и т.н.

Ето защо логаритмите се използват в изчислителната практика (виж раздел 29).

Действието, обратно на логаритъма, се нарича потенциране, а именно: потенцирането е действието, чрез което самото това число се намира чрез дадения логаритъм от число. По същество потенцирането не е някакво специално действие: то се свежда до повишаване на основата на степен (равна на логаритъма на числото). Терминът "потенциране" може да се счита за синоним на термина "потенциране".

При потенциране е необходимо да се използват правилата, които са обратни на правилата за логаритъм: заменете сбора от логаритми с логаритъм от продукта, разликата от логаритми с логаритъм от частното и т.н. По-специално, ако има всеки коефициент пред знака на логаритъма, тогава по време на потенцирането той трябва да бъде прехвърлен към индикаторните градуси под знака на логаритъма.

Пример 5. Намерете N, ако е известно, че

Решение. Във връзка с току-що посоченото правило за потенциране, факторите 2/3 и 1/3, които са пред знаците на логаритмите от дясната страна на това равенство, ще бъдат прехвърлени към показателите под знаците на тези логаритми; получаваме

Сега заместваме разликата на логаритмите с логаритъма на частното:

за да получим последната дроб в тази верига от равенства, ние освободихме предишната дроб от ирационалност в знаменателя (раздел 25).

Свойство 7. Ако основата е по-голяма от едно, тогава по-голямото число има по-голям логаритъм (а по-малкото има по-малък), ако основата е по-малко от едно, тогава по-голямото число има по-малък логаритъм (и по-малкото един има по-голям).

Това свойство се формулира и като правило за логаритъм от неравенства, двете части на които са положителни:

При логаритъм на неравенства с основа, по-голяма от единица, знакът на неравенството се запазва, а при логаритъм с основа, по-малка от единица, знакът на неравенството се обръща (виж също т. 80).

Доказателството се основава на свойства 5 и 3. Разгледайте случая, когато Ако , тогава и, като вземем логаритъм, получаваме

(a и N/M лежат от една и съща страна на единица). Оттук

Следва случай а, читателят сам ще разбере.

Дефиниция на логаритъм

Логаритъмът на числото b при основа a е степента, на която трябва да повдигнете a, за да получите b.

Числото eв математиката е обичайно да се обозначава границата, към която клони изразът

Номер eе ирационално число- число, несъизмеримо с единица, не може да се изрази точно нито като цяло, нито като дроб рационаленномер.

Писмо д- първата буква на латинска дума exonere- да се перчи, откъдето идва и името в математиката експоненциален- експоненциална функция.

Номер дшироко използвани в математиката и във всички науки, по един или друг начин използвайки математически изчисления за своите нужди.

Логаритми. Свойства на логаритмите

Определение: Основният логаритъм на положително число b е степента c, до която трябва да се повдигне числото a, за да се получи числото b.

Основна логаритмична идентичност:

7) Формула за преход към нова база:

lna = log e a, e ≈ 2,718…

Задачи и тестове по темата „Логаритми. Свойства на логаритмите»

• Логаритми - Важни теми за повтаряне на изпита по математика

За да изпълните успешно задачите по тази тема, трябва да знаете определението за логаритъм, свойствата на логаритмите, основното логаритмично тъждество, дефинициите за десетичен и натурален логаритъм. Основните типове задачи по тази тема са задачи за пресмятане и преобразуване на логаритмични изрази. Нека разгледаме тяхното решение на следните примери.

Решение:Използвайки свойствата на логаритмите, получаваме

Решение:използвайки свойствата на степента, получаваме

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Свойства на логаритмите, формулировки и доказателства.

Логаритмите имат редица характерни свойства. В тази статия ще анализираме основните свойства на логаритмите. Тук даваме техните формулировки, записваме свойствата на логаритмите под формата на формули, показваме примери за тяхното приложение и също така даваме доказателства за свойствата на логаритмите.

Навигация в страницата.

Основни свойства на логаритмите, формули

За по-лесно запомняне и използване, представяме основни свойства на логаритмитекато списък с формули. В следващия раздел даваме техните формулировки, доказателства, примери за употреба и необходимите обяснения.

Свойство на журнал на единица: log a 1=0 за всеки a>0, a≠1.

Логаритъмът на число, равно на основата: log a a=1 за a>0 , a≠1 .

Свойство на основен градусен логаритъм: log a a p =p, където a>0, a≠1 и p е всяко реално число.

Логаритъмът на произведението на две положителни числа: log a (x y)=log a x+log a y, a>0, a≠1, x>0, y>0,
и свойството на логаритъма на произведението на n положителни числа: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 >0, …, xn >0 .

Частно свойство на логаритъм: , където a>0 , a≠1 , x>0 , y>0 .

Логаритъм на степен на число: log a b p =p log a |b| , където a>0 , a≠1 , b и p са такива числа, че степента на b p има смисъл и b p >0 .

Последица: , където a>0 , a≠1 , n е естествено число, по-голямо от едно, b>0 .

Следствие 1: , a>0 , a≠1 , b>0 , b≠1 .

Следствие 2: , a>0 , a≠1 , b>0 , p и q са реални числа, q≠0 , по-специално, за b=a имаме .

Справки и доказателства за имоти

Преминаваме към формулирането и доказателството на записаните свойства на логаритмите. Всички свойства на логаритмите се доказват въз основа на определението на логаритъма и основното логаритмично тъждество, което следва от него, както и свойствата на степента.

Да започнем с свойства на логаритъма от единица. Неговата формулировка е следната: логаритъмът от единица е равен на нула, т.е. log a 1=0за всяко a>0, a≠1. Доказателството е просто: тъй като a 0 =1 за всяко a, което удовлетворява горните условия a>0 и a≠1 , тогава доказаното равенство log a 1=0 веднага следва от дефиницията на логаритъма.

Нека дадем примери за приложение на разглежданото свойство: log 3 1=0 , lg1=0 и .

Да преминем към следващото свойство: логаритъма на число, равно на основата, е равен на единица, това е, log a a=1за a>0, a≠1. Наистина, тъй като a 1 =a за всяко a , тогава по дефиницията на логаритъма log a a a=1 .

Примери за използване на това свойство на логаритмите са log 5 5=1 , log 5.6 5.6 и lne=1 .

Логаритъмът на степента на число, равен на основата на логаритъма, е равен на степента. Това свойство на логаритъма съответства на формула на формата log a a p =p, където a>0 , a≠1 и p е всяко реално число. Това свойство следва пряко от дефиницията на логаритъма. Обърнете внимание, че ви позволява незабавно да посочите стойността на логаритъма, ако е възможно да представите числото под знака на логаритъма като степен на основа, ще говорим повече за това в статията за изчисляване на логаритми.

Например log 2 2 7 =7 , log10 -4 =-4 и .

Логаритъм от произведението на две положителни числа x и y е равно на произведението от логаритмите на тези числа: log a (x y)=log a x+log a y, a>0 , a≠1 . Нека докажем свойството на логаритъма на произведението. Поради свойствата на степента a log a x + log a y =a log a x a log a y , и тъй като чрез главното логаритмично тъждество a log a x =x и a log a y =y , тогава a log a x a log a y =x y . Така, a log a x+log a y =x y , откъдето изискваното равенство следва от дефиницията на логаритъма.

Нека покажем примери за използване на свойството на логаритъма на произведението: log 5 (2 3)=log 5 2+log 5 3 и .

Свойството логаритъм на произведението може да се обобщи до произведението на крайно число n от положителни числа x 1 , x 2 , …, x n като log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Това равенство може лесно да се докаже чрез метода на математическата индукция.

Например натуралният логаритъм на произведение може да бъде заменен със сумата от три натурални логаритъма на числата 4, e и .

Логаритъм от частното на две положителни числа x и y е равно на разликата между логаритмите на тези числа. Свойството на частния логаритъм съответства на формула на формата , където a>0 , a≠1 , x и y са някои положителни числа. Валидността на тази формула се доказва като формулата за логаритъм на произведението: тъй като , тогава по дефиницията на логаритъма .

Ето пример за използване на това свойство на логаритъма: .

Да преминем към свойство на логаритъм от степен. Логаритъмът на степента е равен на произведението на степента и логаритъма на модула на основата на тази степен. Записваме това свойство на логаритъма на степента под формата на формула: log a b p =p log a |b|, където a>0 , a≠1 , b и p са такива числа, че степента на b p има смисъл и b p >0 .

Първо доказваме това свойство за положително b. Основната логаритмична идентичност ни позволява да представим числото b като log a b , след това b p =(a log a b) p и полученият израз, поради свойството степен, е равен на a p log a b . Така стигаме до равенството b p =a p log a b , от което по дефиницията на логаритъма заключаваме, че log a b p =p log a b .

Остава да докажем това свойство за отрицателно b. Тук отбелязваме, че изразът log a b p за отрицателно b има смисъл само за четни експоненти p (тъй като стойността на степента b p трябва да е по-голяма от нула, в противен случай логаритъма няма да има смисъл), и в този случай b p =|b| стр. Тогава b p =|b| p =(a log a |b|) p =a p log a |b| , откъдето log a b p =p log a |b| .

Например, и ln(-3) 4 =4 ln|-3|=4 ln3 .

Следва от предишното свойство свойство на логаритъма от корена: логаритъма на корена на n-та степен е равен на произведението на дробта 1/n и логаритъма на корена на израза, т.е. където a>0, a≠1, n е естествено число, по-голямо от едно, b>0.

Доказателството се основава на равенство (вижте дефиницията на експонента с дробна степен), което е валидно за всяко положително b и свойството на логаритъма на степента: .

Ето пример за използване на това свойство: .

Сега да докажем формула за преобразуване към новата основа на логаритъмамил . За да направите това, е достатъчно да докажете валидността на равенството log c b=log a b log c a . Основната логаритмична идентичност ни позволява да представим числото b като log a b, тогава log c b=log c a log a b. Остава да използваме свойството на логаритъма на степента: log c a log a b = log a b log c a . Така се доказва равенството log c b=log a b log c a, което означава, че е доказана и формулата за преминаване към нова основа на логаритъма .

Нека да покажем няколко примера за прилагане на това свойство на логаритмите: и .

Формулата за преминаване към нова база ви позволява да преминете към работа с логаритми, които имат „удобна“ база. Например, може да се използва за превключване към естествени или десетични логаритми, така че да можете да изчислите стойността на логаритъма от таблица с логаритми. Формулата за преход към нова основа на логаритъм също позволява в някои случаи да се намери стойността на даден логаритъм, когато са известни стойностите на някои логаритми с други бази.

Често се използва специален случай на формулата за преход към нова основа на логаритъма за c=b на формата. Това показва, че log a b и log b a са взаимно обратни числа. напр. .

Често се използва и формулата, която е удобна при намиране на логаритмични стойности. За да потвърдим думите си, ще покажем как се изчислява стойността на логаритъма на формата с него. Ние имаме . За да се докаже формулата, е достатъчно да се използва формулата за преход към новата основа на логаритъма a: .

Остава да се докажат сравнителните свойства на логаритмите.

Нека използваме обратния метод. Да предположим, че за a 1 >1 , a 2 >1 и a 1 2 и за 0 1 log a 1 b≤log a 2 b е вярно. Чрез свойствата на логаритмите тези неравенства могат да бъдат пренаписани като И съответно и от тях следва, че log b a 1 ≤log b a 2 и съответно log b a 1 ≥log b a 2. Тогава, по свойствата на степените с еднакви основи, трябва да бъдат изпълнени равенствата b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2, тоест a 1 ≥a 2 . Така сме стигнали до противоречие с условието a 1 2 . Това завършва доказателството.

Основни свойства на логаритмите

• Материали за урока
• Изтеглете всички формули

Логаритмите, като всяко число, могат да се събират, изваждат и преобразуват по всеки възможен начин. Но тъй като логаритмите не са съвсем обикновени числа, тук има правила, които се наричат основни свойства.

Тези правила трябва да се знаят – без тях не може да се реши нито една сериозна логаритмична задача. Освен това има много малко от тях - всичко може да се научи за един ден. Така че да започваме.

Събиране и изваждане на логаритми

Помислете за два логаритма с една и съща основа: log a x и log a y. След това те могат да се събират и изваждат и:

И така, сумата от логаритмите е равна на логаритъма от произведението, а разликата е логаритъма от частното. Моля, обърнете внимание: ключовият момент тук е - същите основания. Ако базите са различни, тези правила не работят!

Тези формули ще помогнат за изчисляване на логаритмичния израз, дори когато отделните му части не се вземат предвид (вижте урока „Какво е логаритъм“). Разгледайте примерите - и вижте:

Задача. Намерете стойността на израза: log 6 4 + log 6 9.

Тъй като основите на логаритмите са еднакви, използваме формулата за сумата:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Задача. Намерете стойността на израза: log 2 48 − log 2 3.

Базите са еднакви, използваме формулата за разликата:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Намерете стойността на израза: log 3 135 − log 3 5.

Отново, основите са същите, така че имаме:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Както можете да видите, оригиналните изрази са съставени от "лоши" логаритми, които не се разглеждат отделно. Но след трансформациите се получават съвсем нормални числа. Много тестове се основават на този факт. Да, този контрол - подобни изрази напълно сериозно (понякога - практически без промени) се предлагат на изпита.

Премахване на експонентата от логаритъма

Сега нека усложним малко задачата. Ами ако има степен в основата или аргумента на логаритъма? Тогава показателят на тази степен може да бъде изваден от знака на логаритъма съгласно следните правила:

• log a x n = n log a x;
• 
• 

Лесно се вижда, че последното правило следва първите две. Но все пак е по-добре да го запомните - в някои случаи това значително ще намали количеството на изчисленията.

Разбира се, всички тези правила имат смисъл, ако се спазва логаритъма на ODZ: a > 0, a ≠ 1, x > 0. И още нещо: научете се да прилагате всички формули не само отляво надясно, но и обратно, т.е. можете да въведете числата преди знака на логаритъма в самия логаритъм. Това е, което най-често се изисква.

Задача. Намерете стойността на израза: log 7 49 6 .

Нека се отървем от степента в аргумента според първата формула:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Задача. Намерете стойността на израза:

[Надпис на фигура]

Забележете, че знаменателят е логаритъм, чиято основа и аргумент са точни степени: 16 = 2 4 ; 49 = 72. Ние имаме:

[Надпис на фигура]

Мисля, че последният пример има нужда от пояснение. Къде изчезнаха логаритмите? До последния момент работим само със знаменателя. Те представиха основата и аргумента на логаритъма, стоящ там под формата на градуси и извадиха индикаторите - получиха „триетажна“ дроб.

Сега нека разгледаме основната фракция. Числителят и знаменателят имат едно и също число: log 2 7. Тъй като log 2 7 ≠ 0, можем да намалим дробта - 2/4 ще остане в знаменателя. Според правилата на аритметиката, четворката може да се прехвърли в числителя, което беше направено. Резултатът е отговорът: 2.

Преход към нова основа

Говорейки за правилата за събиране и изваждане на логаритми, специално подчертах, че те работят само с еднакви основи. Ами ако основите са различни? Ами ако не са точни степени на едно и също число?

Формулите за преход към нова база идват на помощ. Ние ги формулираме под формата на теорема:

Нека е даден логаритъм log a x. Тогава за всяко число c, такова че c > 0 и c ≠ 1, равенството е вярно:

[Надпис на фигура]

По-специално, ако поставим c = x , получаваме:

[Надпис на фигура]

От втората формула следва, че е възможно да се разменят основата и аргументът на логаритъма, но в този случай целият израз се „обръща“, т.е. логаритъма е в знаменателя.

Тези формули рядко се срещат в обикновени числови изрази. Възможно е да се оцени колко са удобни само при решаване на логаритмични уравнения и неравенства.

Има обаче задачи, които изобщо не могат да бъдат решени, освен чрез преминаване към нова основа. Нека разгледаме няколко от тях:

Задача. Намерете стойността на израза: log 5 16 log 2 25.

Обърнете внимание, че аргументите на двата логаритма са точни показатели. Нека извадим индикаторите: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Сега нека обърнем втория логаритъм:

[Надпис на фигура]

Тъй като произведението не се променя от пермутация на множители, ние спокойно умножихме четири и две и след това изчислихме логаритмите.

Задача. Намерете стойността на израза: log 9 100 lg 3.

Основата и аргументът на първия логаритъм са точни степени. Нека го запишем и да се отървем от индикаторите:

[Надпис на фигура]

Сега нека се отървем от десетичния логаритъм, като преминем към нова основа:

[Надпис на фигура]

Основно логаритмично тъждество

Често в процеса на решаване се изисква да се представи число като логаритъм на дадена основа. В този случай формулите ще ни помогнат:

1. n = log a a n

2. В първия случай числото n става експонента в аргумента. Числото n може да бъде абсолютно всичко, защото е само стойността на логаритъма.

   Втората формула всъщност е перифразирана дефиниция. Нарича се основно логаритмично тъждество.

   Наистина, какво ще стане, ако числото b се повдигне на такава степен, че числото b на тази степен дава числото a? Точно така: това е същото число a . Прочетете внимателно този параграф отново - много хора "висят" на него.

   Подобно на новите формули за базово преобразуване, основната логаритмична идентичност понякога е единственото възможно решение.

   [Надпис на фигура]

   Обърнете внимание, че log 25 64 = log 5 8 - просто вземете квадрата на основата и аргумента на логаритъма. Като се имат предвид правилата за умножение на степени с една и съща основа, получаваме:

   [Надпис на фигура]

   Ако някой не е наясно, това беше истинска задача от Единния държавен изпит 🙂

   Логаритмична единица и логаритмична нула

   В заключение ще дам две тъждества, които е трудно да наречем свойства - по-скоро това са следствия от дефиницията на логаритъма. Постоянно се намират в проблеми и учудващо създават проблеми дори на "напредналите" ученици.

   1. log a a = 1 е логаритмичната единица. Запомнете веднъж завинаги: логаритъмът при всяка основа а от самата тази основа е равен на едно.
   2. log a 1 = 0 е логаритмична нула. Основата a може да бъде всякаква, но ако аргументът е единица - логаритъма е нула! Тъй като 0 = 1 е пряко следствие от определението.

   Това са всички имоти. Не забравяйте да се упражнявате да ги прилагате на практика! Изтеглете мамения лист в началото на урока, разпечатайте го - и решете проблемите.

   Логаритъм. Свойства на логаритъма (събиране и изваждане).

   Свойства на логаритъмаследват от определението му. И така, логаритъма на числото bпо разум Адефинирана като степенна степен, до която трябва да се повдигне число аза да получите номера b(логаритъмът съществува само за положителни числа).

   От тази формулировка следва, че изчислението x=log a b, е еквивалентно на решаването на уравнението брадва=b.Например, log 2 8 = 3защото 8 = 2 3 . Формулировката на логаритъма дава възможност да се обоснове, че ако b=a c, след това логаритъма на числото bпо разум аравно на с. Също така е ясно, че темата за логаритъма е тясно свързана с темата за степента на числото.

   С логаритмите, както с всички числа, можете да изпълнявате операции събиране, изважданеи трансформирайте по всякакъв възможен начин. Но с оглед на факта, че логаритмите не са съвсем обикновени числа, тук важат техните собствени специални правила, които се наричат основни свойства.

   Събиране и изваждане на логаритми.

   Вземете два логаритма с една и съща основа: дневник xИ log a y. След това премахнете възможно е да извършвате операции за събиране и изваждане:

   Както виждаме, сбор от логаритмие равно на логаритъма на произведението и разлика логаритми- логаритъма на частното. И това е вярно, ако числата А, ХИ приположителен и а ≠ 1.

   Важно е да се отбележи, че основният аспект в тези формули са едни и същи бази. Ако основите се различават една от друга, тези правила не важат!

   Правилата за събиране и изваждане на логаритми с еднакви основи се четат не само отляво надясно, но и обратно. В резултат на това имаме теоремите за логаритъм от произведението и логаритъм от частното.

   Логаритъм на произведениетодве положителни числа е равно на сумата от техните логаритми ; перифразирайки тази теорема, получаваме следното, ако числата А, хИ приположителен и а ≠ 1, Че:

   Логаритъм на частнотона две положителни числа е равно на разликата между логаритмите на делителя и делителя. С други думи, ако числата А, хИ приположителен и а ≠ 1, Че:

   Прилагаме горните теореми за решаване примери:

   Ако числата хИ притогава са отрицателни формула за логаритъм на произведениестава безсмислено. Така че е забранено да се пише:

   тъй като изразите log 2 (-8) и log 2 (-4) изобщо не са дефинирани (логаритмичната функция при= дневник 2 хопределени само за положителни стойности на аргумента х).

   Теорема за произведениее приложим не само за два, но и за неограничен брой фактори. Това означава, че за всеки естествен ки всякакви положителни числа х 1 , х 2 , . . . ,x nима идентичност:

   от теореми за частен логаритъмможе да се получи още едно свойство на логаритъма. Добре известно е, че лог а 1= 0, следователно,

   Така че има равенство:

   Логаритми на две взаимно реципрочни числана една и съща основа ще се различават един от друг само по знак. Така:

   Логаритъм. Свойства на логаритмите

   Логаритъм. Свойства на логаритмите

   Помислете за равенството. Уведомете ни стойностите и искаме да намерим стойността на .

   Тоест, ние търсим степенна степен, към която трябва да се обърнете, за да получите .

   Позволявам променливата може да приеме произволна реална стойност, тогава върху променливите се налагат следните ограничения: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Ако знаем стойностите на и и сме изправени пред задачата да намерим неизвестното, тогава за тази цел се въвежда математическа операция, която се нарича логаритъм.

   За да намерим стойността, която вземаме логаритъм от числоот фондация :

   Логаритъмът на число към основата е степента, до която трябва да повдигнете, за да получите.

   Това е основно логаритмично тъждество:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   е по същество математическа нотация дефиниции на логаритъм.

   Математическата операция логаритъм е обратната на степенуването, така че свойства на логаритмитеса тясно свързани със свойствата на степента.

   Изброяваме основните свойства на логаритмите:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Следната група от свойства ви позволява да представите показателя на израза под знака на логаритъма или стоящ в основата на логаритъма като коефициент преди знака на логаритъма:

   6.

   7.

   8.

   9.

   Следващата група формули ви позволява да преминете от логаритъм с дадена основа към логаритъм с произволна основа и се нарича формули за преход към нова база:

   10.

   12. (следствие от свойство 11)

   

   Следните три свойства не са добре известни, но често се използват при решаване на логаритмични уравнения или при опростяване на изрази, съдържащи логаритми:

   13.

   14.

   15.

   Специални случаи:

   — десетичен логаритъм

   — натурален логаритъм

   При опростяване на изрази, съдържащи логаритми, се прилага общ подход:

   1. Представяме десетичните дроби под формата на обикновени.

   2. Представяме смесените числа като неправилни дроби.

   3. Числата в основата на логаритъма и под знака на логаритъма се разлагат на прости множители.

   4. Опитваме се да приведем всички логаритми към една и съща основа.

   5. Приложете свойствата на логаритмите.

   Нека да разгледаме примери за опростяване на изрази, съдържащи логаритми.

   Пример 1

   Изчисли:

   Нека опростим всички показатели: нашата задача е да ги доведем до логаритми, чиято основа е същото число като основата на степента.

   ==(по свойство 7)=(по свойство 6) =

   Заместете показателите, които сме получили в оригиналния израз. Получаваме:

   Отговор: 5,25

   Пример 2 Изчислете:

   

   Привеждаме всички логаритми към база 6 (в този случай логаритмите от знаменателя на фракцията ще „мигрират“ към числителя):

   Нека разложим числата под знака на логаритъма на прости множители:

   Приложете свойства 4 и 6:

   Представяме замяната

   Получаваме:

   Отговор: 1

   Логаритъм . Основно логаритмично тъждество.

   Свойства на логаритмите. Десетичен логаритъм. натурален логаритъм.

   логаритъм положително число N в основата (b > 0, b 1) се нарича експонента x, на която трябва да повдигнете b, за да получите N .

   Този запис е еквивалентен на следното: b x = N .

   ПРИМЕРИ: log 3 81 = 4, тъй като 3 4 = 81 ;

   log 1/3 27 = – 3, защото (1/3) - 3 = 3 3 = 27 .

   Горната дефиниция на логаритъма може да бъде записана като идентичност:

   

   Основни свойства на логаритмите.

   2) log 1 = 0 защото b 0 = 1 .

   3) Логаритъмът на произведението е равен на сумата от логаритмите на факторите:

   4) Логаритъмът на частното е равен на разликата между логаритмите на делителя и делителя:

   5) Логаритъмът на степента е равен на произведението на експонентата и логаритъма на нейната основа:

   Последствието от това свойство е следното: дневник корен е равно на логаритъма от коренното число, разделено на степента на корена:

   

   6) Ако основата на логаритъма е степен, тогава стойността реципрочната стойност на експонента може да бъде извадена от знака на дневника на римата:

   

   Последните две свойства могат да бъдат комбинирани в едно:

   

   7) Формулата за преходния модул (т.е. прехода от една основа на логаритъма към друга база):

   

   В конкретен случай, когато N = ание имаме:

   

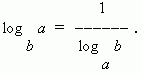
   Десетичен логаритъм Наречен основен логаритъм 10. Означава се с lg, т.е. дневник 10 н= дневник н. Логаритми на числата 10, 100, 1000, . p са съответно 1, 2, 3, …, т.е. има толкова много положителни

   единици, колко нули има в логаритъма след единица. Логаритми на числата 0,1, 0,01, 0,001, . p са съответно –1, –2, –3, …, т.е. има толкова отрицателни единици, колкото нули има в логаритмичното число преди единицата (включително нула цели числа). Логаритмите на останалите числа имат дробна част, наречена мантиса. Цялата част от логаритъма се нарича Характеристика. За практически приложения най-удобни са десетичните логаритми.

   натурален логаритъм Наречен основен логаритъм д. Означава се с ln, т.е. дневник д н=вн н. Номер де ирационален, приблизителната му стойност е 2,718281828. Това е границата, към която числото (1 + 1 / н) нс неограничено увеличение н(см. първата прекрасна границана страницата Ограничения на числовата последователност).
   Колкото и странно да изглежда, естествените логаритми се оказаха много удобни при извършване на различни операции, свързани с анализа на функциите. Изчисляване на основни логаритми дмного по-бързо от всяка друга основа.

• Какво ви е необходимо днес, за да осиновите дете в Русия? Осиновяването в Русия, в допълнение към отговорното лично решение, включва редица процедури за държавна проверка на кандидатите. Твърдият подбор на подготвителния етап допринася за повече […]
• Безплатна информация по TIN или OGRN от данъчния регистър в цяла Русия - онлайн На Единния портал на данъчните услуги информация за държавна регистрация на юридически лица, индивидуални предприемачи, […]
• Наказание за шофиране без документи (шофьорска книжка, застраховка, STS) Понякога, поради забрава, шофьорите сядат зад волана без книжка и получават глоба за шофиране без документи. Припомняме, че шофьор, шофирал с него непременно […]
• Цветя за мъже. Какви цветя можете да подарите на мъж? Какви цветя могат да се подарят на мъж? Няма толкова много "мъжки" цветя, но има такива, които се подаряват на мъже. Малък списък с цветя пред вас: Хризантеми. Рози. Карамфили. […]
• Бележката е специална форма на документ, който се използва във вътрешната среда на предприятието и служи за бързо решаване на текущи производствени проблеми. Обикновено този документ се изготвя с цел извършване на някои […]
• Кога и как да получите финансираната част от пенсията в Сбербанк? Сбербанк е банка партньор на държавния пенсионен фонд. Въз основа на това гражданите, издали капиталова пенсия, биха могли да прехвърлят капиталовата […]
• Детски надбавки в Уляновск и района на Уляновск през 2018 г. Освен това във всички региони действат програми, одобрени от федералния закон. Да видим кой и на какви ползи може да разчита. Като регионални власти […]
• Подробно ръководство за изготвяне на пълномощно за представляване на интересите на физическо лице в съда В гражданско или арбитражно дело, в административно или наказателно дело интересите както на ищеца, така и на ответника могат да бъдат представлявани от адвокат: […]

основни свойства.

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

същите основания

log6 4 + log6 9.

Сега нека усложним малко задачата.

Примери за решаване на логаритми

Ами ако има степен в основата или аргумента на логаритъма? Тогава показателят на тази степен може да бъде изваден от знака на логаритъма съгласно следните правила:

Разбира се, всички тези правила имат смисъл, ако се спазва логаритъма на ODZ: a > 0, a ≠ 1, x >

Задача. Намерете стойността на израза:

Преход към нова основа

Нека е даден логаритъм logax. Тогава за всяко число c, такова че c > 0 и c ≠ 1, равенството е вярно:

Задача. Намерете стойността на израза:

Вижте също:

Основни свойства на логаритъма

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Показателят е 2,718281828…. За да запомните показателя, можете да изучите правилото: показателят е 2,7 и два пъти годината на раждане на Лев Толстой.

Основни свойства на логаритмите

Познавайки това правило, вие ще знаете както точната стойност на експонента, така и датата на раждане на Лев Толстой.

Примери за логаритми

Вземете логаритъм на изразите

Пример 1
А). x=10ac^2 (a>0, c>0).

По свойства 3,5 изчисляваме

2.

3.

4. Където .

Пример 2 Намерете x if

Пример 3. Нека е дадена стойността на логаритмите

Изчислете log(x), ако

Основни свойства на логаритмите

Логаритмите, като всяко число, могат да се събират, изваждат и преобразуват по всеки възможен начин. Но тъй като логаритмите не са съвсем обикновени числа, тук има правила, които се наричат основни свойства.

Тези правила трябва да се знаят – без тях не може да се реши нито една сериозна логаритмична задача. Освен това има много малко от тях - всичко може да се научи за един ден. Така че да започваме.

Събиране и изваждане на логаритми

Помислете за два логаритма с една и съща основа: logax и logay. След това те могат да се събират и изваждат и:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

И така, сумата от логаритмите е равна на логаритъма от произведението, а разликата е логаритъма от частното. Моля, обърнете внимание: ключовият момент тук е - същите основания. Ако базите са различни, тези правила не работят!

Тези формули ще помогнат за изчисляване на логаритмичния израз, дори когато отделните му части не се вземат предвид (вижте урока „Какво е логаритъм“). Разгледайте примерите и вижте:

Тъй като основите на логаритмите са еднакви, използваме формулата за сумата:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Задача. Намерете стойността на израза: log2 48 − log2 3.

Базите са еднакви, използваме формулата за разликата:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Задача. Намерете стойността на израза: log3 135 − log3 5.

Отново, основите са същите, така че имаме:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Както можете да видите, оригиналните изрази са съставени от "лоши" логаритми, които не се разглеждат отделно. Но след трансформациите се получават съвсем нормални числа. Много тестове се основават на този факт. Да, контрол - подобни изрази с цялата сериозност (понякога - практически без промени) се предлагат на изпита.

Премахване на експонентата от логаритъма

Лесно се вижда, че последното правило следва първите две. Но все пак е по-добре да го запомните - в някои случаи това значително ще намали количеството на изчисленията.

Разбира се, всички тези правила имат смисъл, ако се спазва логаритъма на ODZ: a > 0, a ≠ 1, x > 0. И още нещо: научете се да прилагате всички формули не само отляво надясно, но и обратно, т.е. можете да въведете числата преди знака на логаритъма в самия логаритъм. Това е, което най-често се изисква.

Задача. Намерете стойността на израза: log7 496.

Нека се отървем от степента в аргумента според първата формула:
log7 496 = 6 log7 49 = 6 2 = 12

Задача. Намерете стойността на израза:

Обърнете внимание, че знаменателят е логаритъм, чиято основа и аргумент са точни степени: 16 = 24; 49 = 72. Имаме:

Мисля, че последният пример има нужда от пояснение. Къде изчезнаха логаритмите? До последния момент работим само със знаменателя.

Формули на логаритми. Логаритмите са примери за решения.

Те представиха основата и аргумента на логаритъма, стоящ там под формата на градуси и извадиха индикаторите - получиха „триетажна“ дроб.

Сега нека разгледаме основната фракция. Числителят и знаменателят имат едно и също число: log2 7. Тъй като log2 7 ≠ 0, можем да намалим дробта - 2/4 ще остане в знаменателя. Според правилата на аритметиката, четворката може да се прехвърли в числителя, което беше направено. Резултатът е отговорът: 2.

Преход към нова основа

Говорейки за правилата за събиране и изваждане на логаритми, специално подчертах, че те работят само с еднакви основи. Ами ако основите са различни? Ами ако не са точни степени на едно и също число?

Формулите за преход към нова база идват на помощ. Ние ги формулираме под формата на теорема:

Нека е даден логаритъм logax. Тогава за всяко число c, такова че c > 0 и c ≠ 1, равенството е вярно:

По-специално, ако поставим c = x, получаваме:

От втората формула следва, че е възможно да се разменят основата и аргументът на логаритъма, но в този случай целият израз се „обръща“, т.е. логаритъма е в знаменателя.

Тези формули рядко се срещат в обикновени числови изрази. Възможно е да се оцени колко са удобни само при решаване на логаритмични уравнения и неравенства.

Има обаче задачи, които изобщо не могат да бъдат решени, освен чрез преминаване към нова основа. Нека разгледаме няколко от тях:

Задача. Намерете стойността на израза: log5 16 log2 25.

Обърнете внимание, че аргументите на двата логаритма са точни показатели. Нека извадим индикаторите: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Сега нека обърнем втория логаритъм:

Тъй като произведението не се променя от пермутация на множители, ние спокойно умножихме четири и две и след това изчислихме логаритмите.

Задача. Намерете стойността на израза: log9 100 lg 3.

Основата и аргументът на първия логаритъм са точни степени. Нека го запишем и да се отървем от индикаторите:

Сега нека се отървем от десетичния логаритъм, като преминем към нова основа:

Основно логаритмично тъждество

Често в процеса на решаване се изисква да се представи число като логаритъм на дадена основа. В този случай формулите ще ни помогнат:

В първия случай числото n става експонента в аргумента. Числото n може да бъде абсолютно всичко, защото е само стойността на логаритъма.

Втората формула всъщност е перифразирана дефиниция. Нарича се така:

Наистина, какво ще се случи, ако числото b се повдигне до такава степен, че числото b в тази степен дава числото a? Точно така: това е същото число a. Прочетете внимателно този параграф отново - много хора „висят“ върху него.

Подобно на новите формули за базово преобразуване, основната логаритмична идентичност понякога е единственото възможно решение.

Задача. Намерете стойността на израза:

Обърнете внимание, че log25 64 = log5 8 - току-що извади квадрата от основата и аргумента на логаритъма. Като се имат предвид правилата за умножение на степени с една и съща основа, получаваме:

Ако някой не е наясно, това беше истинска задача от Единния държавен изпит 🙂

Логаритмична единица и логаритмична нула

В заключение ще дам две тъждества, които е трудно да наречем свойства - по-скоро това са следствия от дефиницията на логаритъма. Постоянно се намират в проблеми и учудващо създават проблеми дори на "напредналите" ученици.

1. logaa = 1 е. Запомнете веднъж завинаги: логаритъмът при всяка основа а от самата тази основа е равен на едно.
2. log 1 = 0 е. Основата a може да бъде всякаква, но ако аргументът е единица, логаритъма е нула! Тъй като a0 = 1 е пряко следствие от определението.

Това са всички имоти. Не забравяйте да се упражнявате да ги прилагате на практика! Изтеглете измамника в началото на урока, разпечатайте го и решете задачите.

Вижте също:

Логаритъмът на числото b при основа a означава израза. Да се ​​изчисли логаритъма означава да се намери такава мощност x (), при която равенството е вярно

Основни свойства на логаритъма

Горните свойства трябва да се знаят, тъй като на тяхна основа почти всички задачи и примери се решават въз основа на логаритми. Останалите екзотични свойства могат да бъдат извлечени чрез математически манипулации с тези формули

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

При изчисляване формулите за сумата и разликата на логаритмите (3.4) се срещат доста често. Останалите са малко сложни, но в редица задачи са незаменими за опростяване на сложни изрази и изчисляване на техните стойности.

Често срещани случаи на логаритми

Някои от често срещаните логаритми са тези, при които основата е дори десет, експоненциална или двойка.
Логаритъмът с основа десет обикновено се нарича логаритъм с основа десет и се обозначава просто lg(x).

От протокола се вижда, че в протокола не са записани осн. Например

Натуралният логаритъм е логаритъмът, чиято основа е степента (означена като ln(x)).

Показателят е 2,718281828…. За да запомните показателя, можете да изучите правилото: показателят е 2,7 и два пъти годината на раждане на Лев Толстой. Познавайки това правило, вие ще знаете както точната стойност на експонента, така и датата на раждане на Лев Толстой.

И друг важен логаритъм по основа две е

Производната на логаритъма на функцията е равна на единица, разделена на променливата

Интегралният или първообразният логаритъм се определя от зависимостта

Горният материал е достатъчен, за да решите широк клас задачи, свързани с логаритми и логаритми. За да асимилирам материала, ще дам само няколко общи примера от училищната програма и университетите.

Примери за логаритми

Вземете логаритъм на изразите

Пример 1
А). x=10ac^2 (a>0, c>0).

По свойства 3,5 изчисляваме

2.
По свойството разлика на логаритмите имаме

3.
Използвайки свойства 3.5 намираме

4. Където .

Привидно сложен израз, използващ серия от правила, се опростява до формата

Намиране на логаритмични стойности

Пример 2 Намерете x if

Решение. За изчислението прилагаме свойства 5 и 13 до последния член

Заместник в записа и скърби

Тъй като основите са равни, приравняваме изразите

Логаритми. Първо ниво.

Нека е дадена стойността на логаритмите

Изчислете log(x), ако

Решение: Вземете логаритъм на променливата, за да запишете логаритъма чрез сумата от членовете

Това е само началото на запознаването с логаритмите и техните свойства. Практикувайте изчисления, обогатете практическите си умения - скоро ще имате нужда от придобитите знания за решаване на логаритмични уравнения. След като изучихме основните методи за решаване на такива уравнения, ще разширим знанията ви за друга също толкова важна тема - логаритмични неравенства ...

Основни свойства на логаритмите

Логаритмите, като всяко число, могат да се събират, изваждат и преобразуват по всеки възможен начин. Но тъй като логаритмите не са съвсем обикновени числа, тук има правила, които се наричат основни свойства.

Тези правила трябва да се знаят – без тях не може да се реши нито една сериозна логаритмична задача. Освен това има много малко от тях - всичко може да се научи за един ден. Така че да започваме.

Събиране и изваждане на логаритми

Помислете за два логаритма с една и съща основа: logax и logay. След това те могат да се събират и изваждат и:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

И така, сумата от логаритмите е равна на логаритъма от произведението, а разликата е логаритъма от частното. Моля, обърнете внимание: ключовият момент тук е - същите основания. Ако базите са различни, тези правила не работят!

Тези формули ще помогнат за изчисляване на логаритмичния израз, дори когато отделните му части не се вземат предвид (вижте урока „Какво е логаритъм“). Разгледайте примерите и вижте:

Задача. Намерете стойността на израза: log6 4 + log6 9.

Тъй като основите на логаритмите са еднакви, използваме формулата за сумата:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Задача. Намерете стойността на израза: log2 48 − log2 3.

Базите са еднакви, използваме формулата за разликата:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Задача. Намерете стойността на израза: log3 135 − log3 5.

Отново, основите са същите, така че имаме:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Както можете да видите, оригиналните изрази са съставени от "лоши" логаритми, които не се разглеждат отделно. Но след трансформациите се получават съвсем нормални числа. Много тестове се основават на този факт. Да, контрол - подобни изрази с цялата сериозност (понякога - практически без промени) се предлагат на изпита.

Премахване на експонентата от логаритъма

Сега нека усложним малко задачата. Ами ако има степен в основата или аргумента на логаритъма? Тогава показателят на тази степен може да бъде изваден от знака на логаритъма съгласно следните правила:

Лесно се вижда, че последното правило следва първите две. Но все пак е по-добре да го запомните - в някои случаи това значително ще намали количеството на изчисленията.

Разбира се, всички тези правила имат смисъл, ако се спазва логаритъма на ODZ: a > 0, a ≠ 1, x > 0. И още нещо: научете се да прилагате всички формули не само отляво надясно, но и обратно, т.е. можете да въведете числата преди знака на логаритъма в самия логаритъм.

Как се решават логаритми

Това е, което най-често се изисква.

Задача. Намерете стойността на израза: log7 496.

Нека се отървем от степента в аргумента според първата формула:
log7 496 = 6 log7 49 = 6 2 = 12

Задача. Намерете стойността на израза:

Обърнете внимание, че знаменателят е логаритъм, чиято основа и аргумент са точни степени: 16 = 24; 49 = 72. Имаме:

Мисля, че последният пример има нужда от пояснение. Къде изчезнаха логаритмите? До последния момент работим само със знаменателя. Те представиха основата и аргумента на логаритъма, стоящ там под формата на градуси и извадиха индикаторите - получиха „триетажна“ дроб.

Сега нека разгледаме основната фракция. Числителят и знаменателят имат едно и също число: log2 7. Тъй като log2 7 ≠ 0, можем да намалим дробта - 2/4 ще остане в знаменателя. Според правилата на аритметиката, четворката може да се прехвърли в числителя, което беше направено. Резултатът е отговорът: 2.

Преход към нова основа

Говорейки за правилата за събиране и изваждане на логаритми, специално подчертах, че те работят само с еднакви основи. Ами ако основите са различни? Ами ако не са точни степени на едно и също число?

Формулите за преход към нова база идват на помощ. Ние ги формулираме под формата на теорема:

Нека е даден логаритъм logax. Тогава за всяко число c, такова че c > 0 и c ≠ 1, равенството е вярно:

По-специално, ако поставим c = x, получаваме:

От втората формула следва, че е възможно да се разменят основата и аргументът на логаритъма, но в този случай целият израз се „обръща“, т.е. логаритъма е в знаменателя.

Тези формули рядко се срещат в обикновени числови изрази. Възможно е да се оцени колко са удобни само при решаване на логаритмични уравнения и неравенства.

Има обаче задачи, които изобщо не могат да бъдат решени, освен чрез преминаване към нова основа. Нека разгледаме няколко от тях:

Задача. Намерете стойността на израза: log5 16 log2 25.

Обърнете внимание, че аргументите на двата логаритма са точни показатели. Нека извадим индикаторите: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Сега нека обърнем втория логаритъм:

Тъй като произведението не се променя от пермутация на множители, ние спокойно умножихме четири и две и след това изчислихме логаритмите.

Задача. Намерете стойността на израза: log9 100 lg 3.

Основата и аргументът на първия логаритъм са точни степени. Нека го запишем и да се отървем от индикаторите:

Сега нека се отървем от десетичния логаритъм, като преминем към нова основа:

Основно логаритмично тъждество

Често в процеса на решаване се изисква да се представи число като логаритъм на дадена основа. В този случай формулите ще ни помогнат:

В първия случай числото n става експонента в аргумента. Числото n може да бъде абсолютно всичко, защото е само стойността на логаритъма.

Втората формула всъщност е перифразирана дефиниция. Нарича се така:

Наистина, какво ще се случи, ако числото b се повдигне до такава степен, че числото b в тази степен дава числото a? Точно така: това е същото число a. Прочетете внимателно този параграф отново - много хора „висят“ върху него.

Подобно на новите формули за базово преобразуване, основната логаритмична идентичност понякога е единственото възможно решение.

Задача. Намерете стойността на израза:

Обърнете внимание, че log25 64 = log5 8 - току-що извади квадрата от основата и аргумента на логаритъма. Като се имат предвид правилата за умножение на степени с една и съща основа, получаваме:

Ако някой не е наясно, това беше истинска задача от Единния държавен изпит 🙂

Логаритмична единица и логаритмична нула

В заключение ще дам две тъждества, които е трудно да наречем свойства - по-скоро това са следствия от дефиницията на логаритъма. Постоянно се намират в проблеми и учудващо създават проблеми дори на "напредналите" ученици.

1. logaa = 1 е. Запомнете веднъж завинаги: логаритъмът при всяка основа а от самата тази основа е равен на едно.
2. log 1 = 0 е. Основата a може да бъде всякаква, но ако аргументът е единица, логаритъма е нула! Тъй като a0 = 1 е пряко следствие от определението.

Това са всички имоти. Не забравяйте да се упражнявате да ги прилагате на практика! Изтеглете измамника в началото на урока, разпечатайте го и решете задачите.