D(f)- тези стойности, които аргументът може да приеме, т.е. функционален обхват.

E(f)- тези стойности, които функцията може да приеме, т.е. набор от функционални стойности.

Методи за намиране на диапазоните на функциите.

последователно намиране на стойности на аргументи на сложна функция;

точкуване/граничен метод;

използване на свойствата на непрекъснатост и монотонност на функция;

използване на дериват;

използване на най-големите и най-малките стойности на функцията;

графичен метод;

метод за въвеждане на параметър;

метод на обратната функция.

Нека разгледаме някои от тях.

Използване на производната

Общ подходза намиране на набор от стойности на непрекъсната функция f(x) е да се намерят най-голямата и най-малката стойност на функцията f(x) в нейната област (или да се докаже, че едната или и двете не съществуват) .

Ако трябва да намерите набор от стойности на функция на сегмента:

намерете производната на дадената функция f "(x);

намерете критичните точки на функцията f(x) и изберете тези, които принадлежат на дадения сегмент;

изчисляване на стойностите на функцията в краищата на сегмента и в избрани критични точки;

сред намерените стойности изберете най-малката и най-голямата стойност;

Наборът от стойности на функцията се заключава между тези стойности.

Ако обхватът на функцията е интервал, тогава се използва същата схема, но вместо стойностите в краищата се използват границите на функцията, когато аргументът клони към краищата на интервала. Граничните стойности от не са включени в набора от стойности.

Метод на граница/резултат

За да намерите набора от стойности на функцията, първо намерете набора от стойности на аргумента и след това намерете съответните минимални и максимални стойности на функцията. С помощта на неравенства - определете границите.

Същността е да се оцени непрекъснатата функция отдолу и отгоре и да се докаже, че функцията достига долната и горната граница на оценките. В този случай съвпадението на набора от стойности на функцията с интервала от долната граница на оценката до горната се определя от непрекъснатостта на функцията и липсата на други стойности за нея.

Свойства на непрекъсната функция

Друг вариант е функцията да се преобразува в непрекъсната монотонна функция, след което с помощта на свойствата на неравенствата се оценява наборът от стойности на новополучената функция.

Последователно намиране на стойности на сложни функционални аргументи

Въз основа на последователното търсене на набор от стойности на междинни функции, които съставляват функцията

Области на основни елементарни функции

функция	Много ценности
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^(2n)$	E(y) =
$y = \cos(x)$	E(y) = [-1;1]
$y = (\rmtg)\, x$	E(y) = (-∞;+∞)
$y = (\rm ctg)\, x$	E(y) = (-∞;+∞)
$y = \arcsin(x)$	E(y) = [-π/2; π/2]
$y = \arccos(x)$	E(y) =
$y = (\rm arctg)\, x$	E(y) = (-π/2; π/2)
$y = (\rm arcctg)\, x$	E(y) = (0; π)

Примери

Намерете набора от стойности на функцията:

Използване на производната

Намерете областта на дефиниция: D(f)=[-3;3], защото $9-x^(2)\geq 0$

Намерете производната: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0, ако x = 0. f"(x) не съществува, ако $\sqrt(9-x^(2))=0$, т.е. за x = ±3. Получаваме три критични точки: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, две от които съвпадат с краищата на сегмента. Изчислете: f(–3) = 0, f(0) = 3, f(3) = 0. Така най-малката стойност на f(x) е 0, най-голямата стойност е 3.

Отговор: E(f) = .

НЕ се използва производно

Намерете най-голямата и най-малката стойност на функцията:

От $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , тогава:

$f(x)\leq \frac(3)(4)$ за всички x;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ за всички x(защото $|\cos (x)|\leq 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

Отговор: $\frac(3)(4)$ и $-\frac(3)(2)$

Ако решите този проблем с помощта на производни, тогава ще трябва да преодолеете пречките, свързани с факта, че функцията f (x) е дефинирана не на сегмент, а на цялата реална линия.

Използване на метода на границите/оценките

От определението за синус следва, че $-1\leq\sin(x)\leq 1$. След това използваме свойствата на числените неравенства.

$-4\leq - 4\sin(x)\leq 4$, (умножете и трите части на двойното неравенство по -4);

$1\leq 5 - 4\sin(x)\leq 9$ (добавено към трите части на двойното неравенство 5);

Тъй като тази функция е непрекъсната в цялата област на дефиниция, наборът от нейните стойности се намира между най-малката и най-голямата стойност в цялата област на дефиниция, ако има такава.

В този случай множеството от стойности на функцията $y = 5 - 4\sin(x)$ е множеството .

От неравенствата $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ получаваме оценката $$\\ -6\leq y\ лек 6 $ $

За x = p и x = 0 функцията приема стойностите -6 и 6, т.е. достига долната и горната граница. Като линейна комбинация от непрекъснати функции cos(7x) и cos(x), функцията y е непрекъсната по цялата числова ос, следователно, чрез свойството на непрекъсната функция, тя приема всички стойности от -6 до 6 включително , и само тях, тъй като поради неравенствата $- 6\leq y\leq 6$ други стойности са невъзможни за него.

Следователно E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Отговор: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Нека трансформираме израза $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.

Дефиницията на косинус предполага $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

Тъй като тази функция е непрекъсната в цялата област на дефиниция, тогава наборът от нейните стойности е затворен между най-малката и най-голямата стойност, ако има такива, наборът от стойности на функцията $y =\sqrt(2)\ cos((x +\frac(\pi)(4 )))$ е множеството $[-\sqrt(2);\sqrt(2)]$.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

Означаваме $t = 5 – (3^(x)+1)^(2)$, където -∞≤t≤4. По този начин проблемът се свежда до намиране на множеството от стойности на функцията $y = \log_(0,5)(t)$ върху лъча (-∞;4). Тъй като функцията $y = \log_(0,5)(t)$ е дефинирана само за t > 0, нейният набор от стойности на лъча (-∞;4) съвпада с набора от стойности на функция в интервала (0;4), представляваща пресечната точка на лъча (-∞;4) с дефиниционната област (0;+∞) на логаритмичната функция. На интервала (0;4) тази функция е непрекъсната и намаляваща. За t > 0 тя клони към +∞, а за t = 4 приема стойност -2, така че E(y) = (-2, +∞).

Използваме техника, базирана на графично представяне на функция.

След трансформации на функцията имаме: y 2 + x 2 = 25 и y ≥ 0, |x| ≤ 5.

Трябва да си припомним, че $x^(2)+y^(2)=r^(2)$ е уравнението на окръжност с радиус r.

При тези ограничения графиката на това уравнение е горният полукръг с център в началото и радиус, равен на 5. Очевидно е, че E(y) = .

Отговор: E(y) = .

Препратки

Обхватът на функциите в задачите на Единния държавен изпит, Минюк Ирина Борисовна

Съвети за намиране на набора от стойности на функцията, Беляева И., Федорова С.

Намиране на множеството от стойности на функцията

Как да решаваме задачи по математика на приемни изпити, И. И. Мелников, И. Н. Сергеев

GBOU лицей (икономически) с. Исакла

Учител по математика Кузаева В.Н.

2016 г

Справочни материали

Примерен разтворНамерете набор от функционални стойности

Обхват на функцията
е

г - всякакъв брой

Обхват на функцията
е г - всякакъв брой

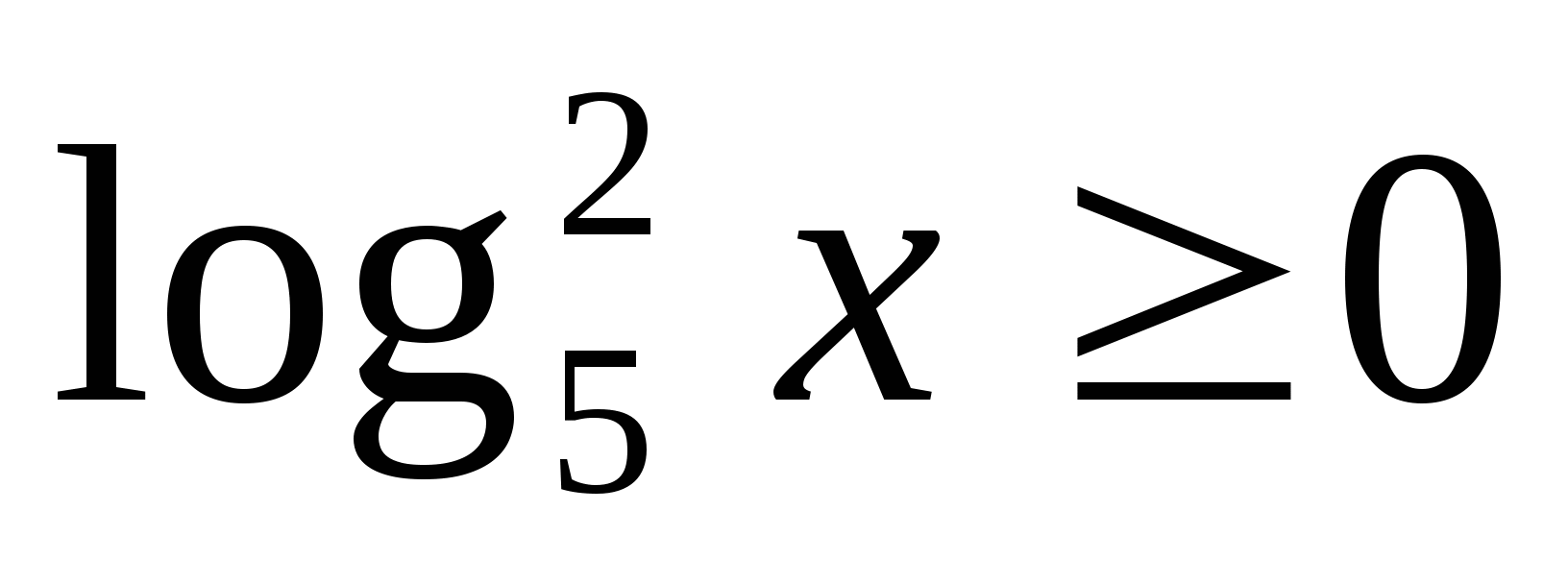
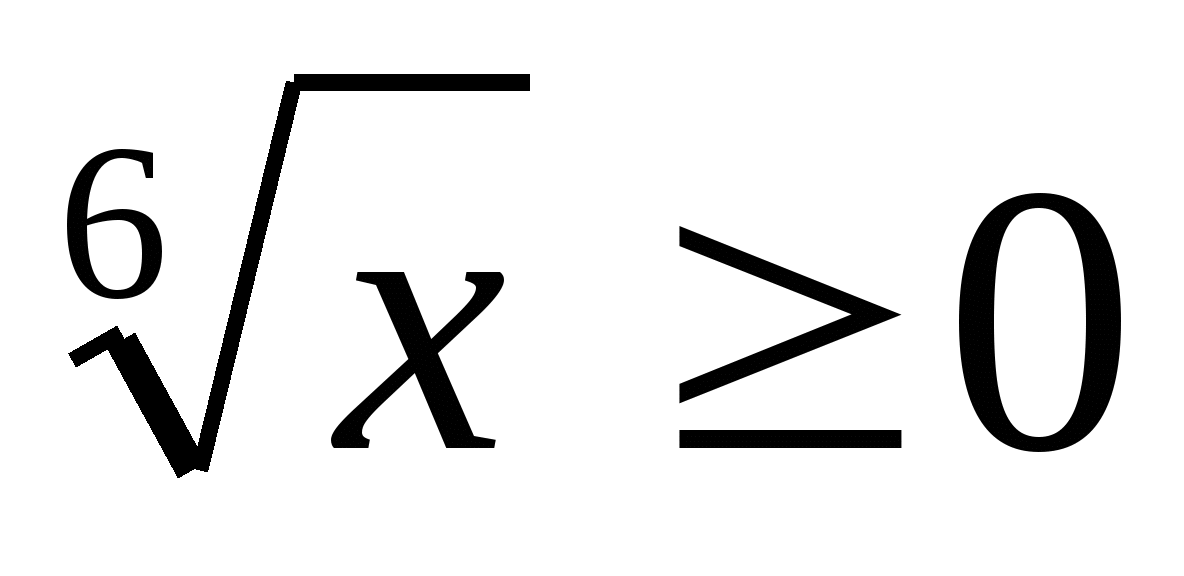
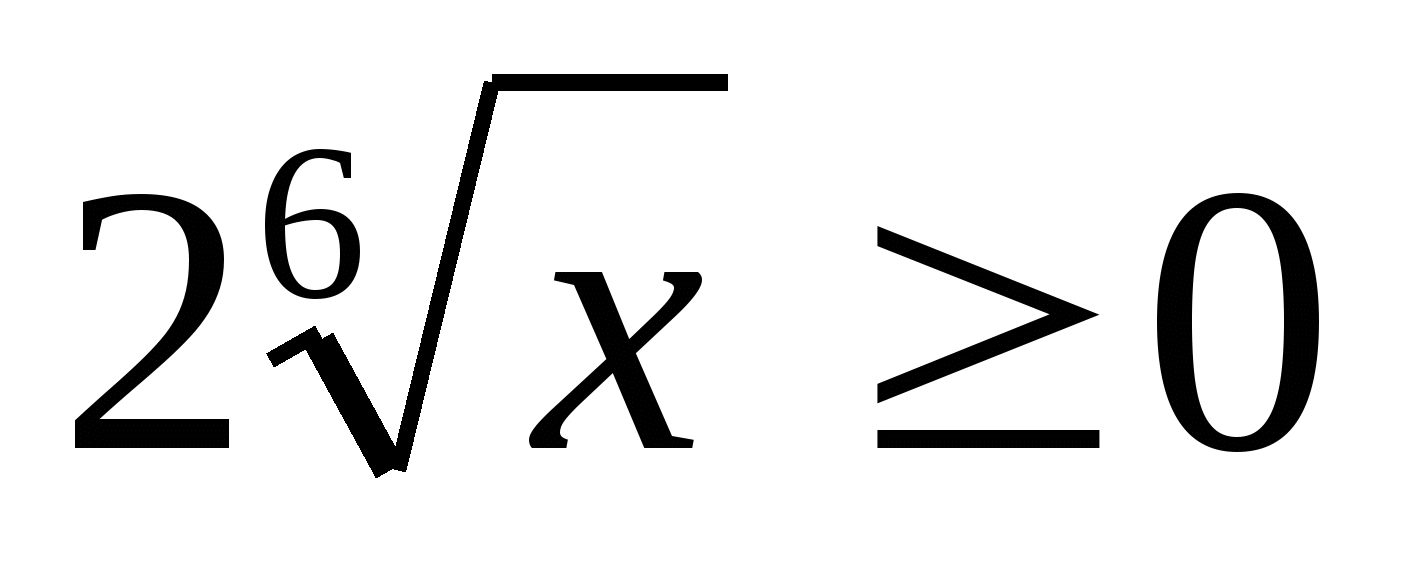
Много ценности

г - всякакъв брой

Най-висока стойност

Най-ниска стойност

Домейн х - всякакъв брой
, където

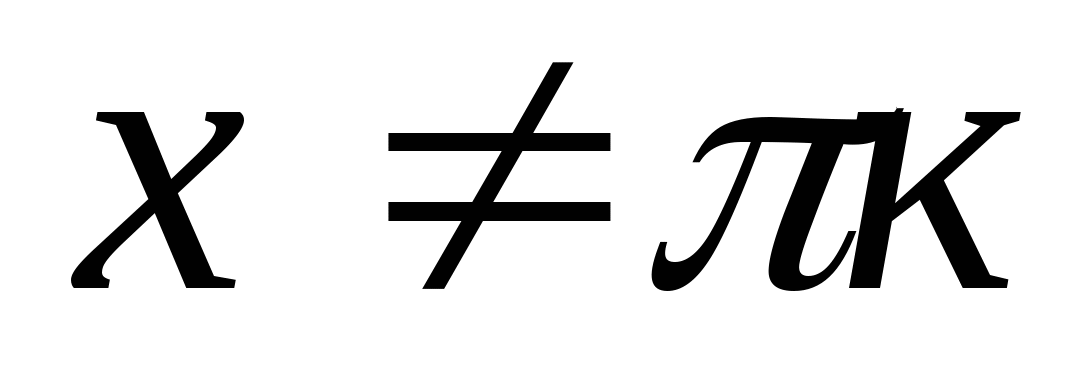, където

Много ценност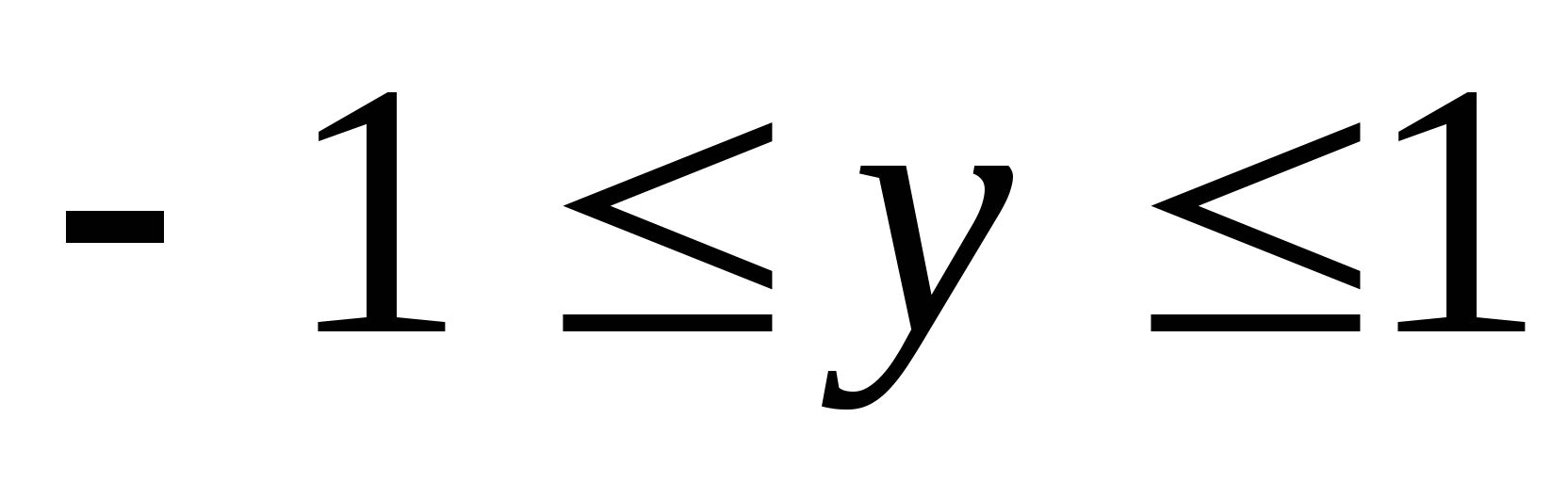и
г - всякакъв бройг - всякакъв брой

Начертайте шаблони за някои тригонометрични функции

Набор от стойности на тригонометрични функции

Опция 1

Y =грях 3x+2.

1) (-5;5) 2) 3) 4) (1;5)

2. Намерете областта на функцията y =tgх + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. Посочете най-малкото цяло число от диапазона на функцията

y = 12,7 + 5 грях(3x-2).

1) -5 2) 8 3) 5 4) 17

5. Посочете функцията, чийто набор от стойности е сегментът [-2;2].

1) y = cos 2x 2) y = грях 2 х 3) г = cos 2 х +2

4) г = 2 грях 4 х

6. Намерете множеството от стойности на функциятаг = tg 2 хна сегмента

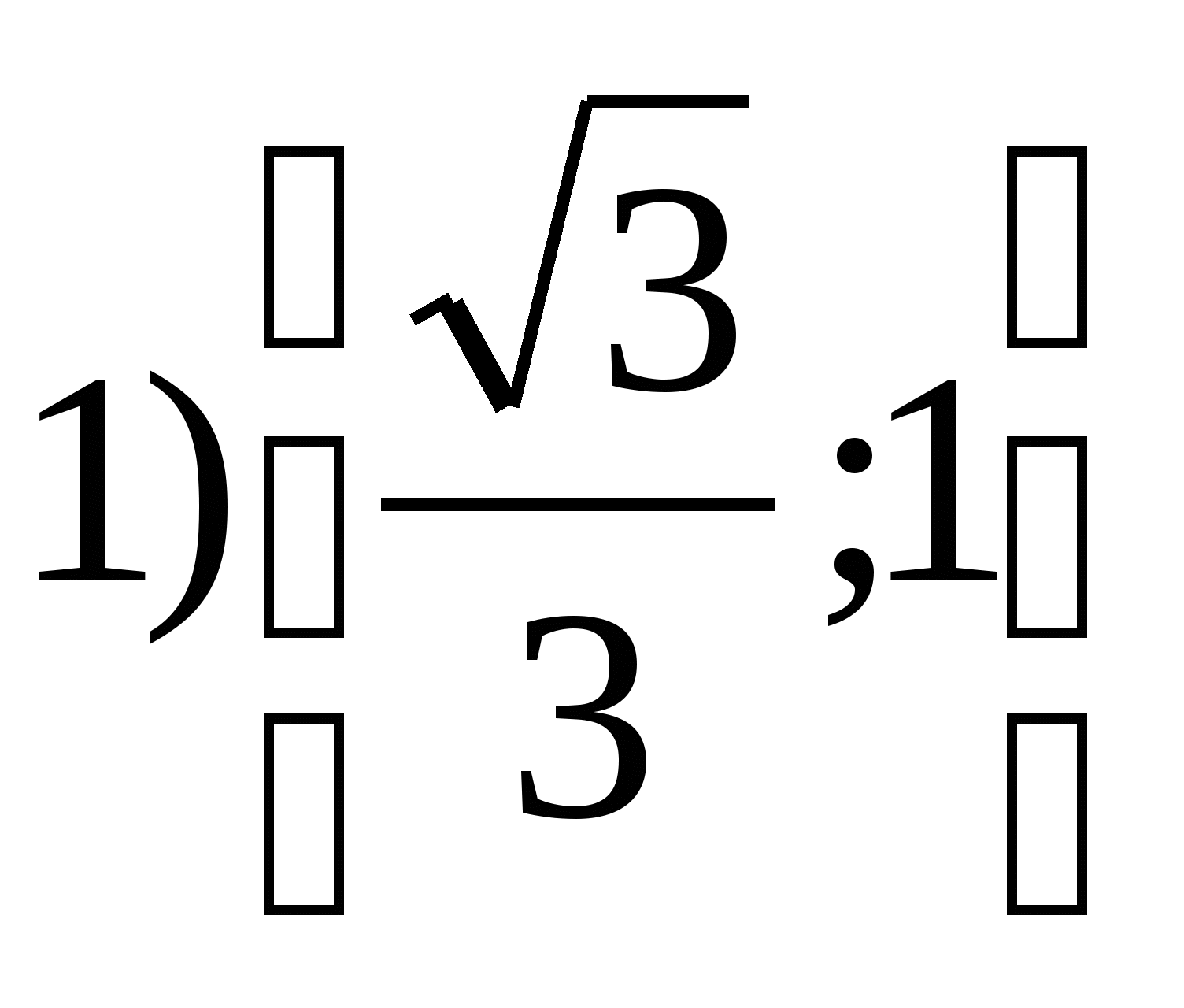
7. Намерете сумата на всички цели числа, които са в диапазона на функциятаг = 4 cos 2 х – 7.

1) -25 2) 25 3) -22 4) 0

Вариант 2

г = 2 cos 5 х +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Намерете обхвата на функцията

1) 3) (-∞;∞) 4) .

3. Посочете най-малкото число от диапазона на функцията

1) 4 2) -3 3) 1 4) -7

4. Посочете най-голямото цяло число от диапазона на функцията

1) 2 2) 13 3) 12 4) -2

5. Посочете функция, чийто набор от стойности е сегментът [-5;5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Намерете множеството от стойности на функцията
на сегмента

7. Намерете произведението на всички цели числа, които са в диапазона на функцията y \u003d 5 - 3грях 2 х.

1) 120 2) 14 3) -15 4) 0

Вариант 3
1. Задайте набор от функционални стойностиг = грях 3 х + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Посочете най-малкото число от диапазона на функцията y = 5tg 2 х+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Посочете функция, чийто набор от стойности е сегмент

[-17;-13].

1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 sin x +10

6. Посочете най-малкото естествено число, което не е включено в множеството от стойности на функцията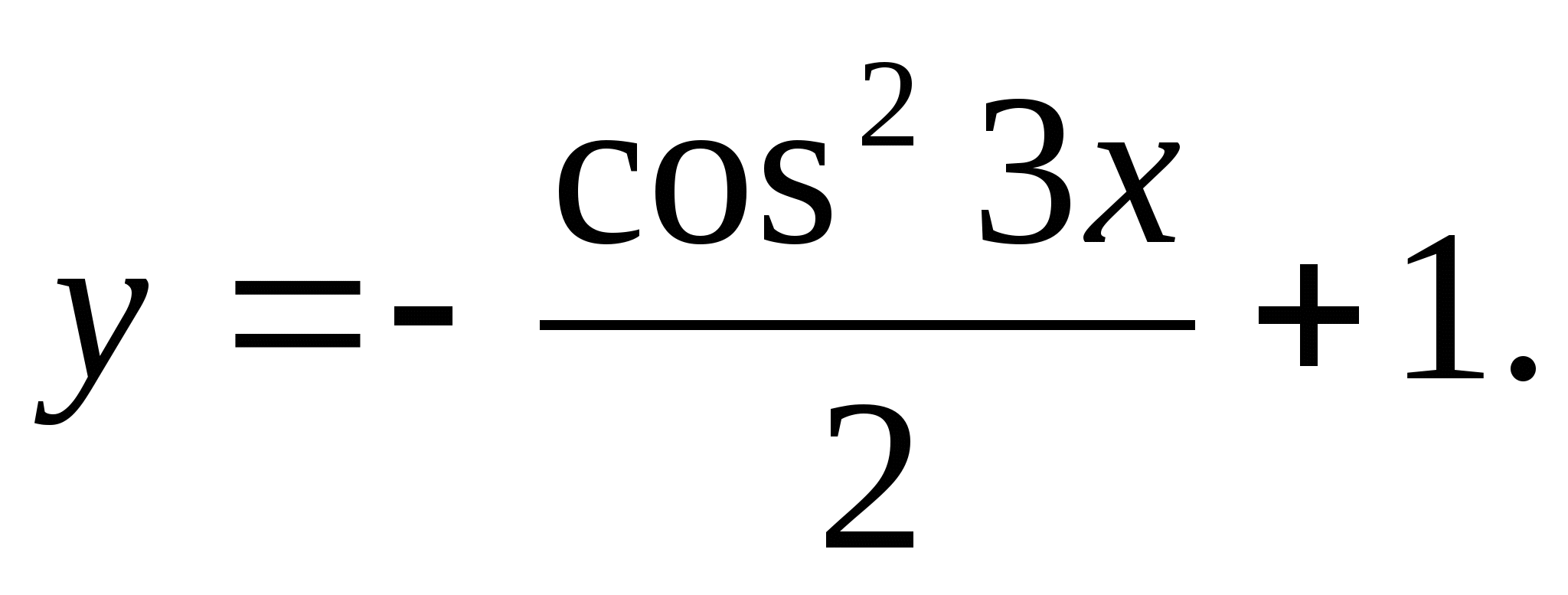

1) 2 2) 4 3) 15 4) 6

7. Колко цели числа принадлежат на множеството от стойности на функцията

г = 2 cos 3 х +10?

1) 2 2) 3 3) 4 5) 5

Вариант 4

1) 2) 4) (-7;-6)

2. Намерете диапазона на функцията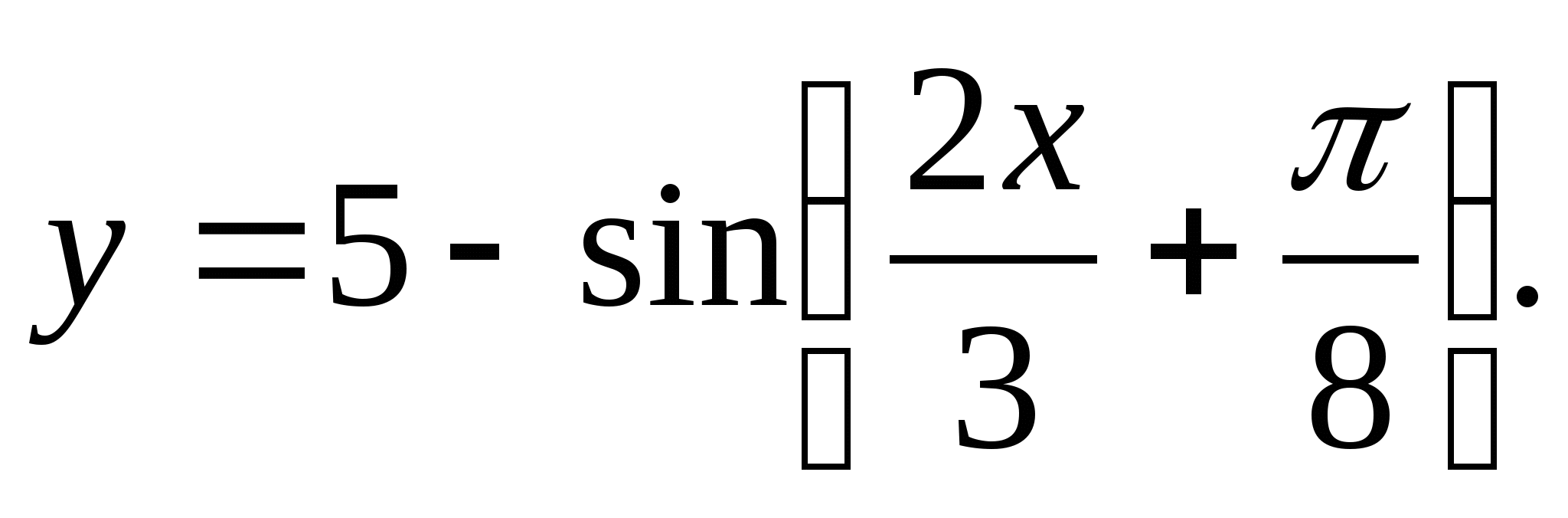

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Посочете най-голямото число от диапазона на функциятаг = -3 ctg 2 х+7.

1) 10 2) 4 3) 7 4) -3

4. Кое от следните числа не е включено в множеството от стойности на функцията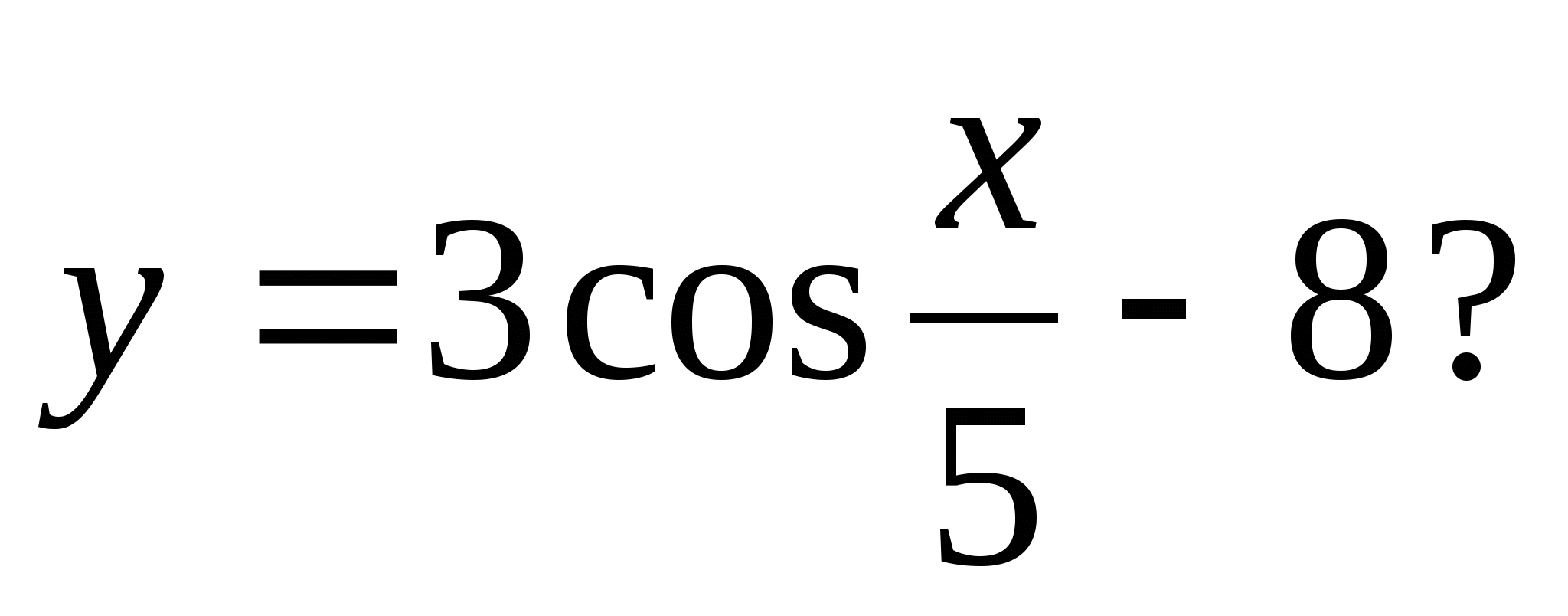

1) -6 2) -5 3) -10 4) -7

5. Посочете функция, чийто набор от стойности е интервалът.

6. Посочете най-голямото цяло отрицателно число, което не е включено в диапазона на функцията

1) -1 2) -25 3) -6 4) -2

7. Колко цели числа принадлежат на множеството от стойности на функцията

1) 11 2) 3 3) 5 4) 4

Вариант 5

1. Посочете набора от стойности на функцията y = 2 -грях 5 х.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Намерете диапазона на функцията

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Посочете най-малкото цяло число от диапазона на функцията

г = 3 + грях 2 2 х.

1) 0 2) 1 3) 3 4) 4

4. Кое от следните числа е включено в множеството от стойности на функцията

1) 128 2) 10,5 3) 3 4) -235

5. Посочете функцията, чийто набор от стойности е сегментът [-9;15].

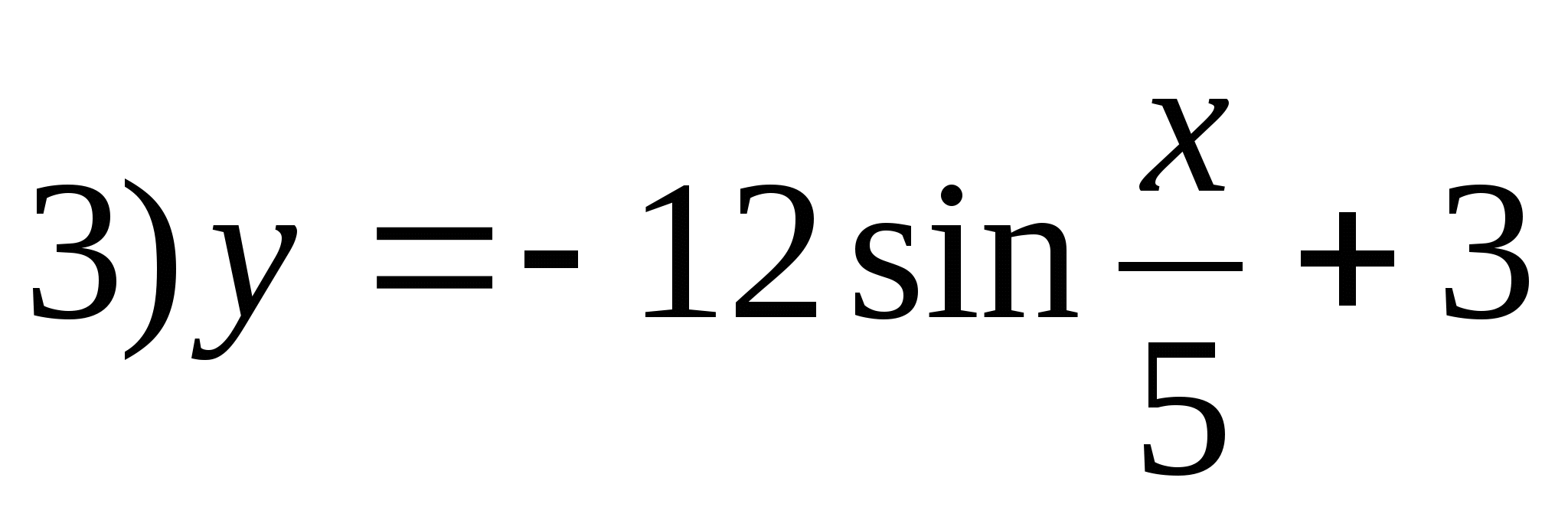
6. Намерете сумата от цели числа, включени в множеството от стойности на функцията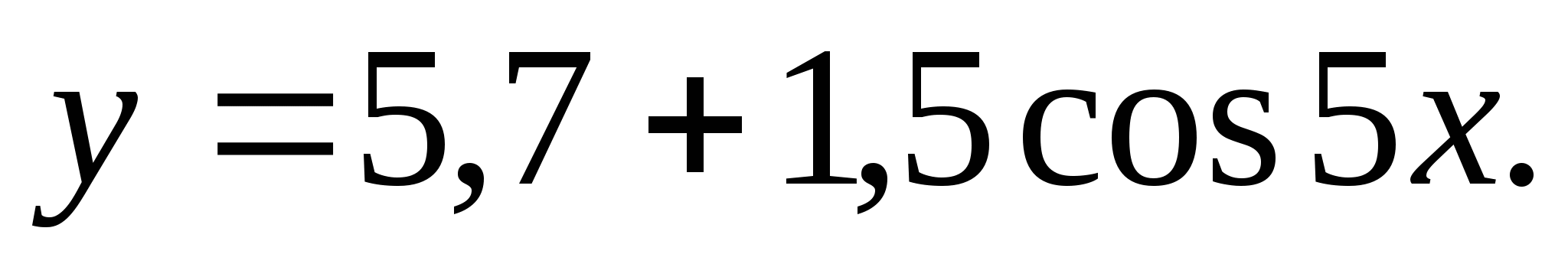

1) 0 2) 7 3) 18 4) 22

7. Намерете най-голямата стойност на функция
на сегмента

1) 0,5 2) 1,5 3) 0 4) 2

Вариант 6

1. Посочете сегмента, съответстващ на набора от стойности на функцията

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Намерете диапазона на функцията

3. Посочете най-голямото число от диапазона на функцията

1) 5 2) -6 3) -3 4) 4

4. Кое от следните числа е включено в множеството от стойности на функцията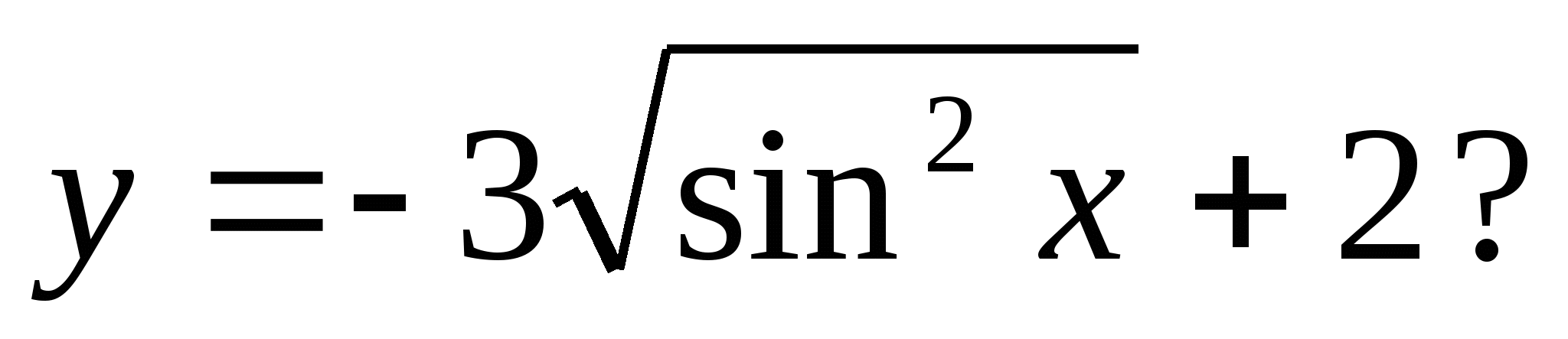

1) 5 2) 0 3) -3 4) 4

5. Посочете функция, чийто набор от стойности е интервалът.

1) при = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) г = 5 cos 4 х 4) г = - tg 2 х + 1

6. Намерете произведението на цели числа, включени в множеството от стойности

г = 3,8 – 1,4 грях 3 х.

1) 17 2) 12 3) 0 4) 60

7. Намерете множеството от стойности на функцията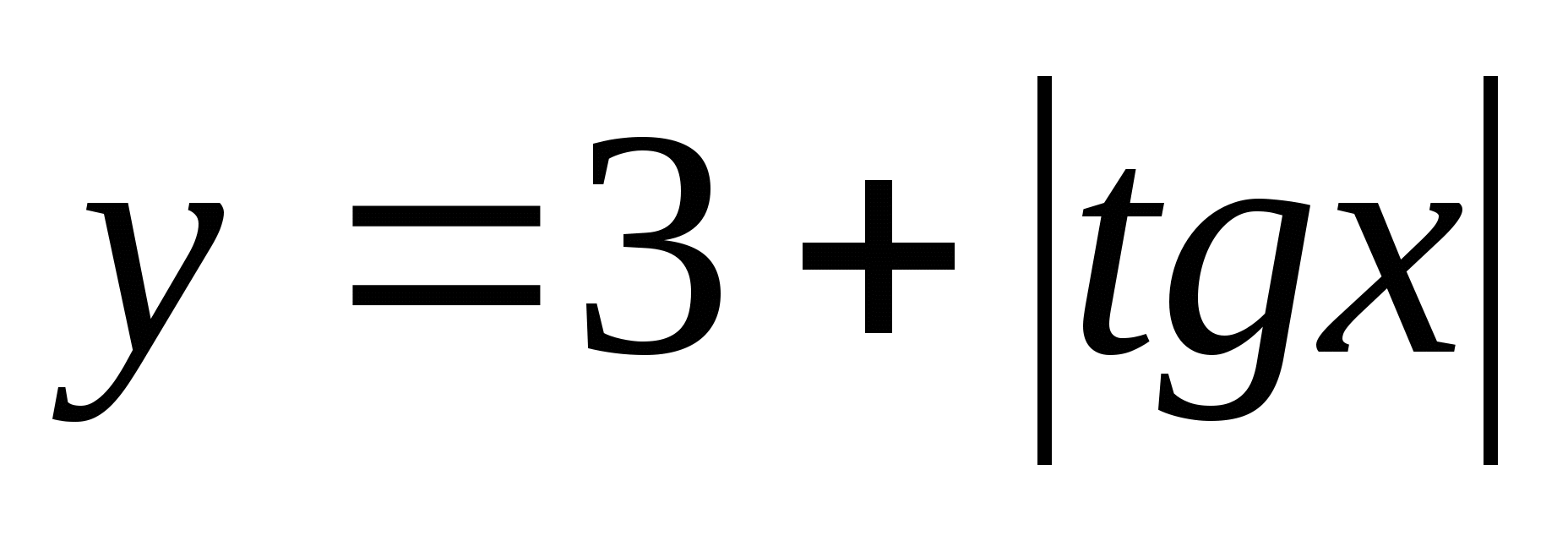
между

1) (3;4) 2) 3)

Вариант 7

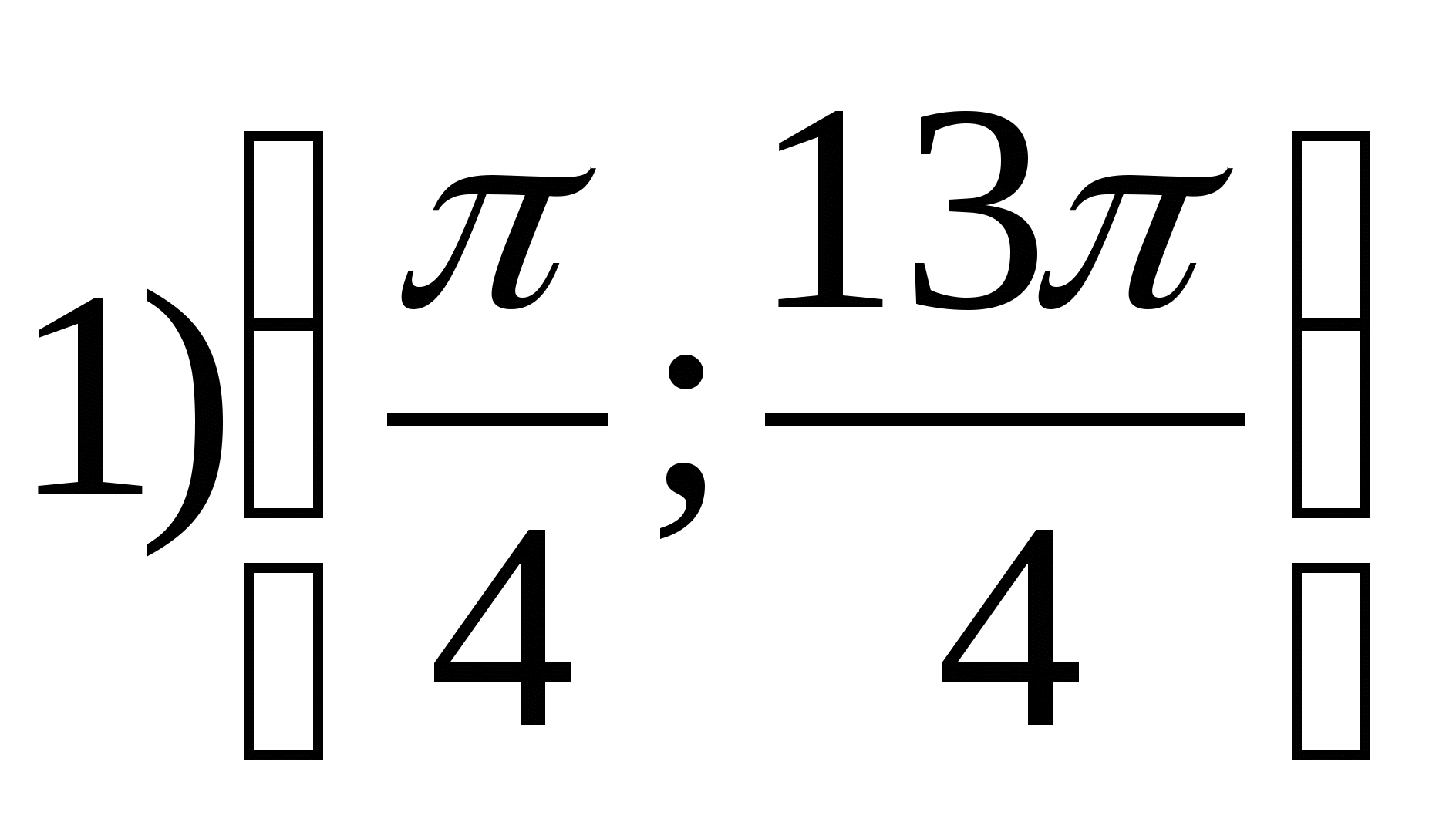
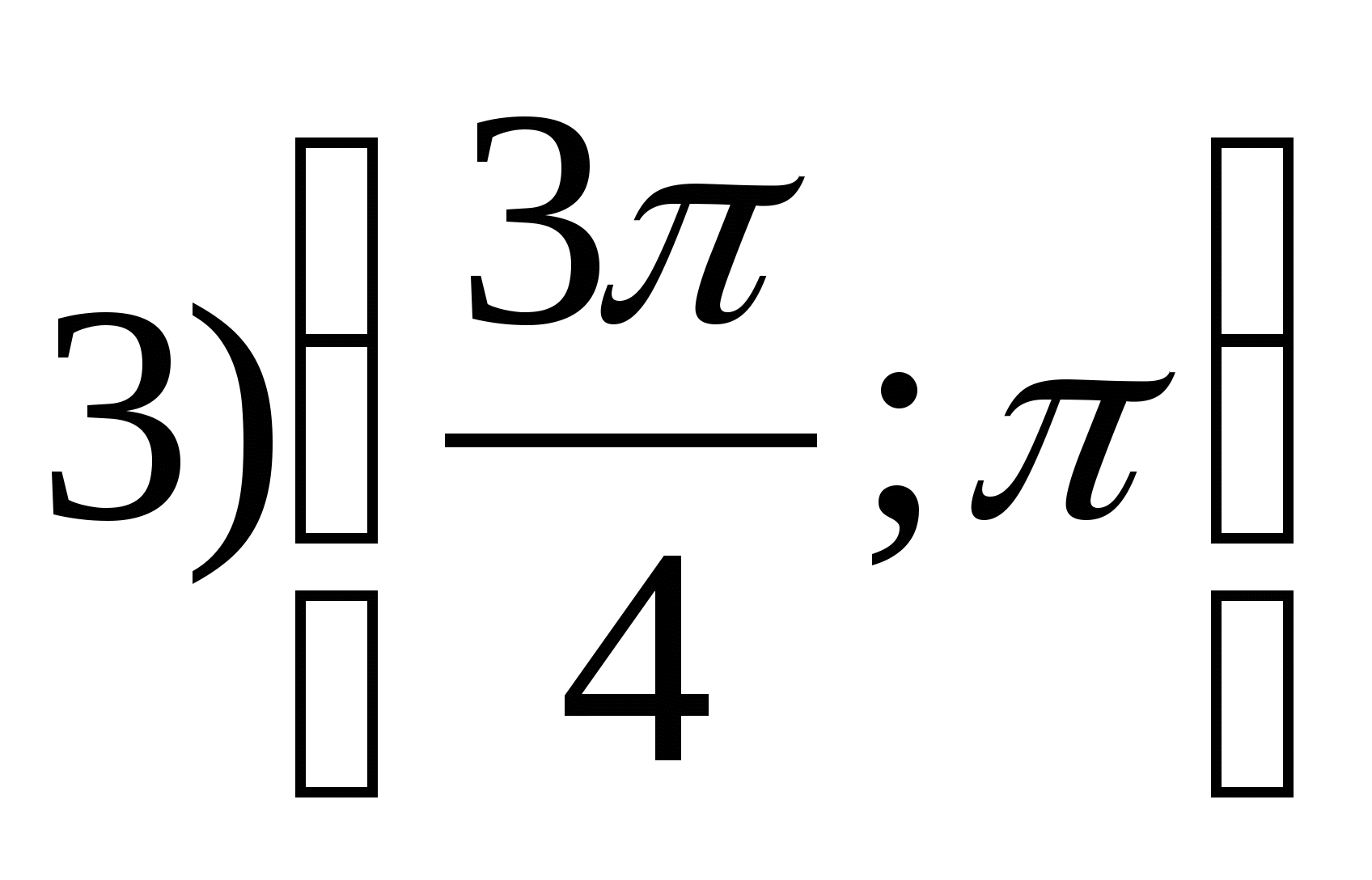
2. Намерете най-малкото цяло число на функцията

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. За какви стойности на a прави уравнениетогрях(3 х-4)+5= аразрешим?

1) 2) 3) (4;6) 4) (-6;4]

грях 2 2 х – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

между

2) 0 3) 1

г = 4 грях(х 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Вариант 8

1. Намерете множеството от стойности на функциятаг = arctgх- 2π.

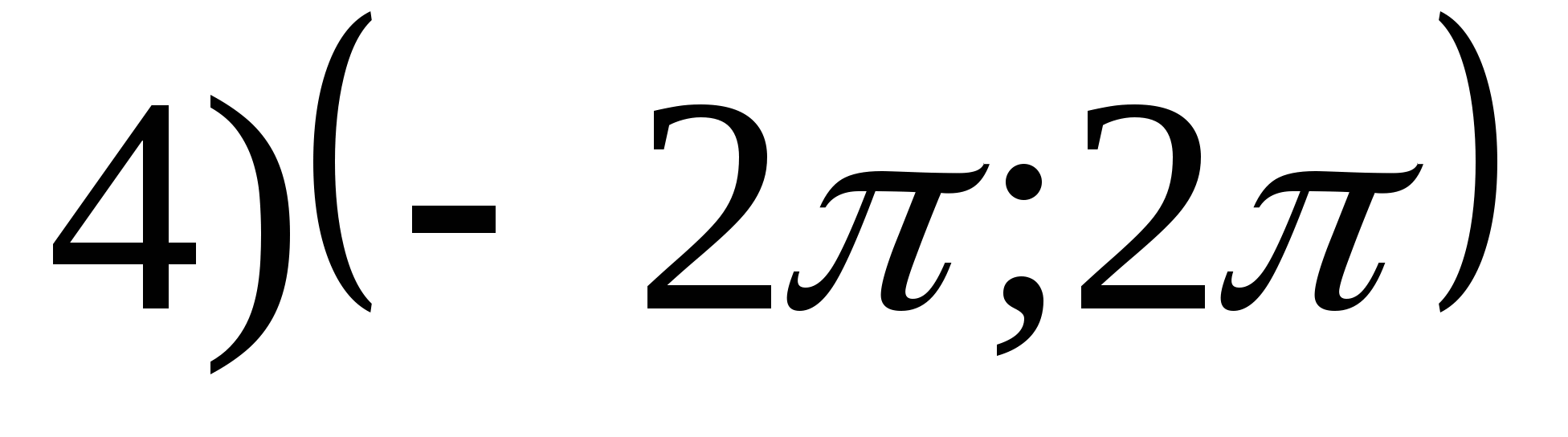
2. Намерете най-голямата стойност на функцията

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Кое от следните числа може да бъде стойност на функцията

1) -4 2) -2 3) 0 4) 2

4. За какви стойности на p уравнение -2+cos(4 х-1)= стрима ли корени?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Намерете множеството от стойности на функциятаг = -2 tg 2 х + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

между
.

1) 0 2) 1 3) -1 4) 3

7. Колко цели числа има в диапазона на функцията

1) 4 2) 3 3) 5 4) 2

Вариант 9

1. Намерете диапазона на функцията

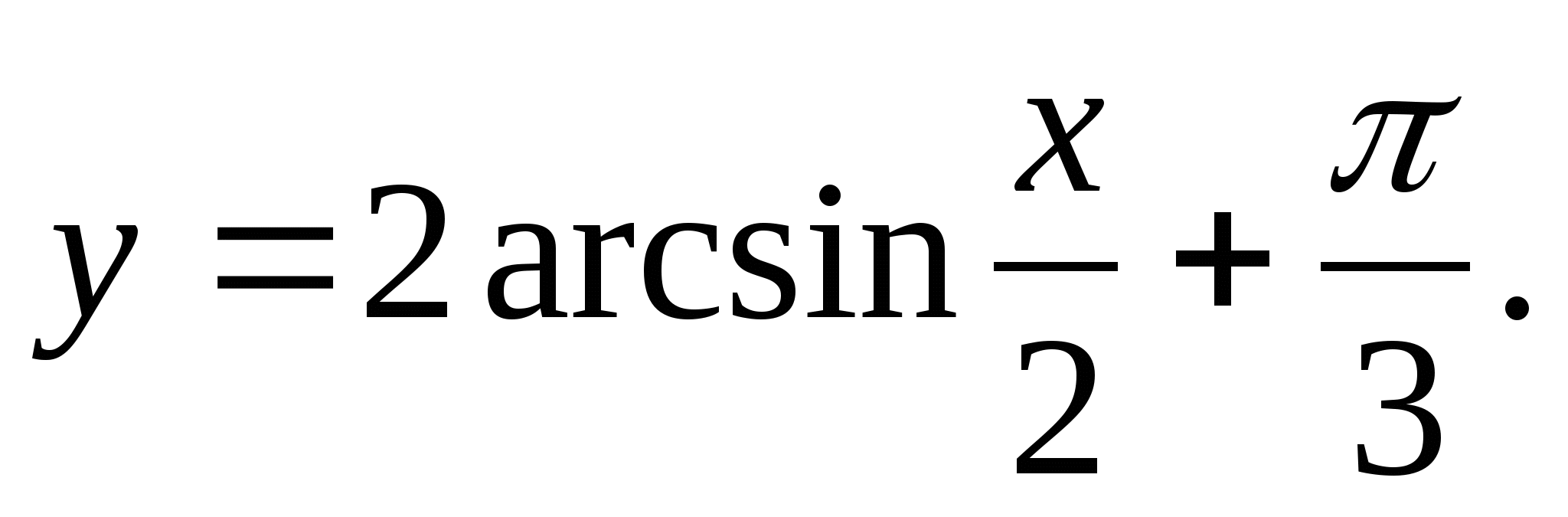
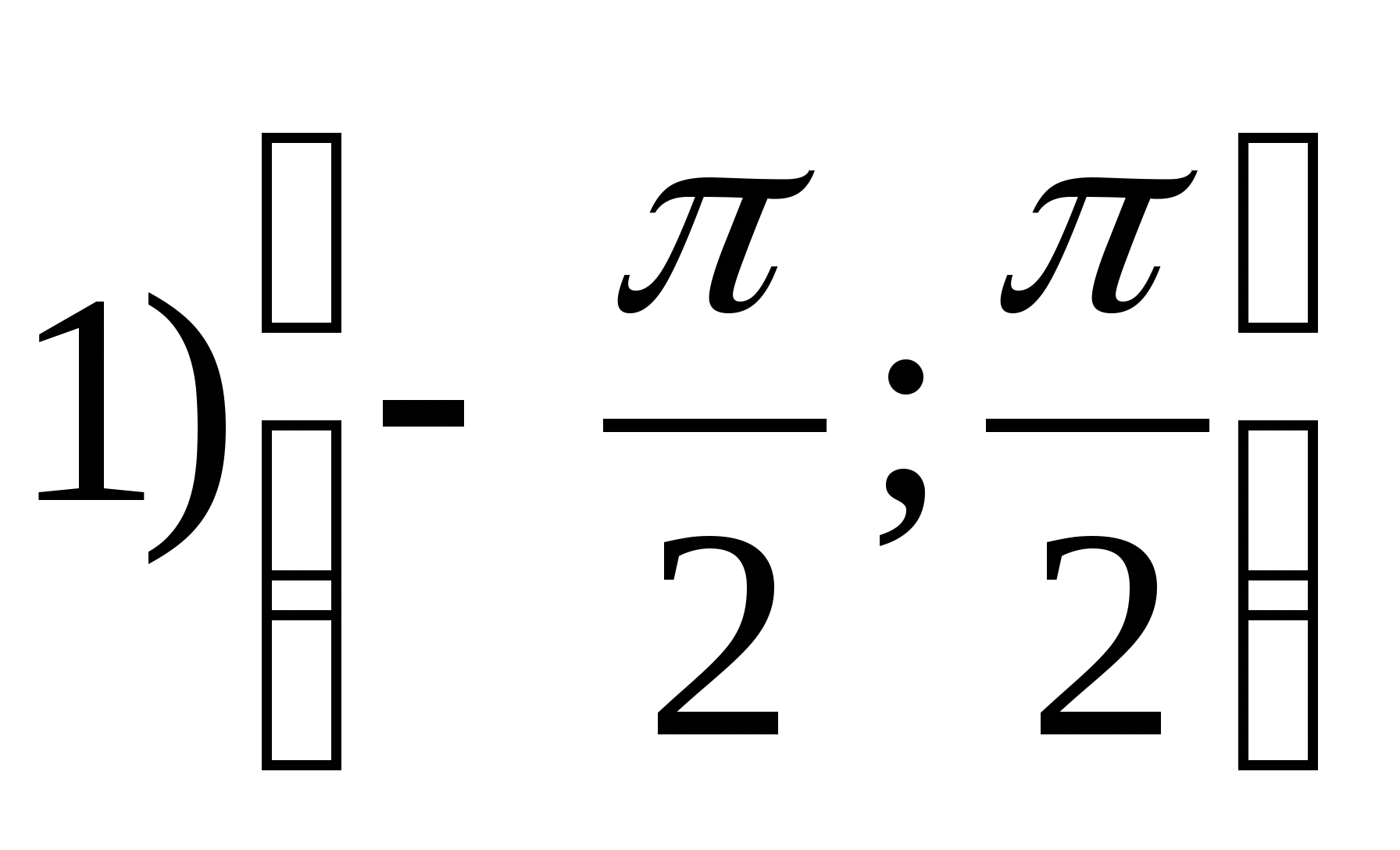
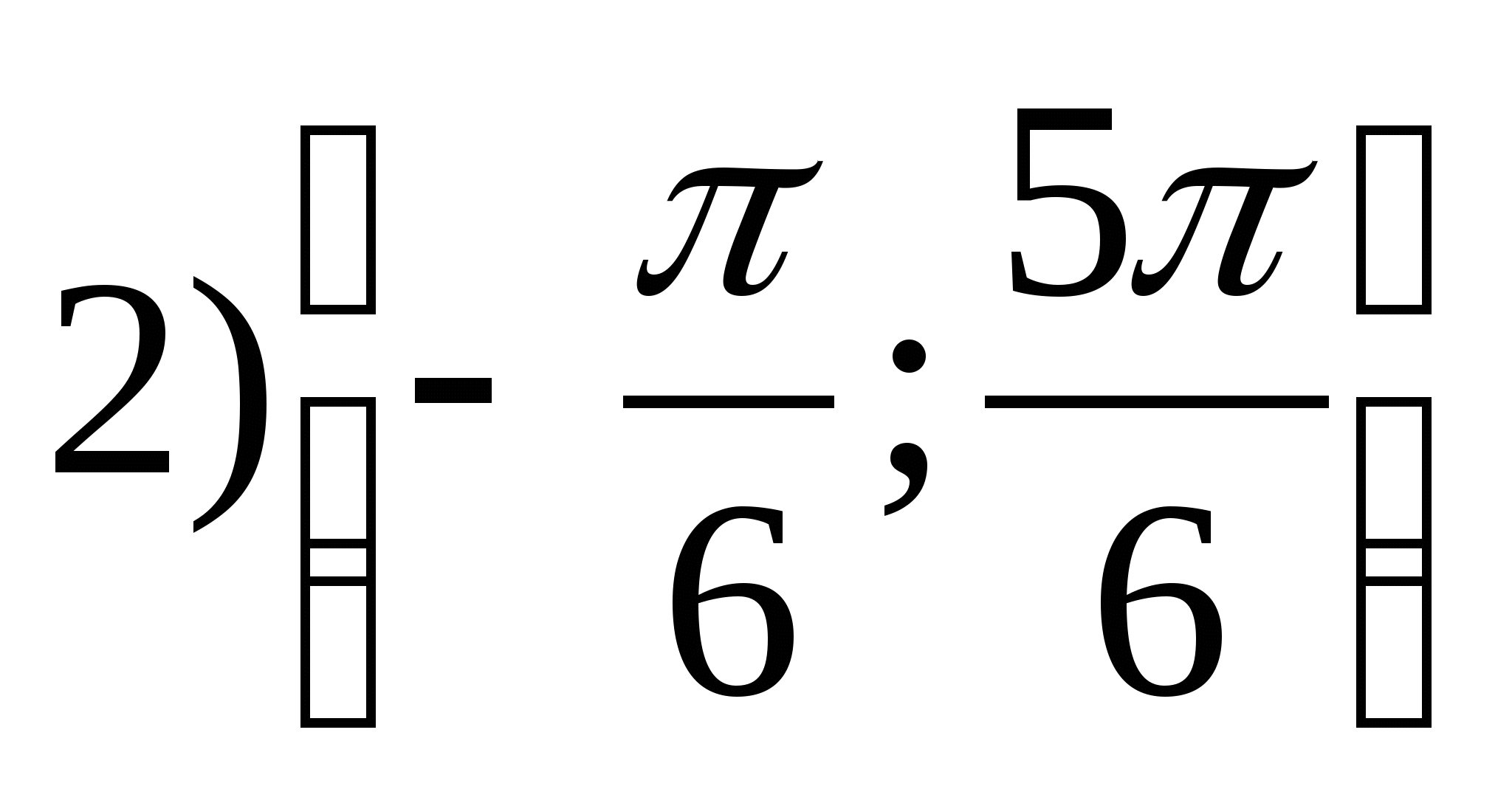
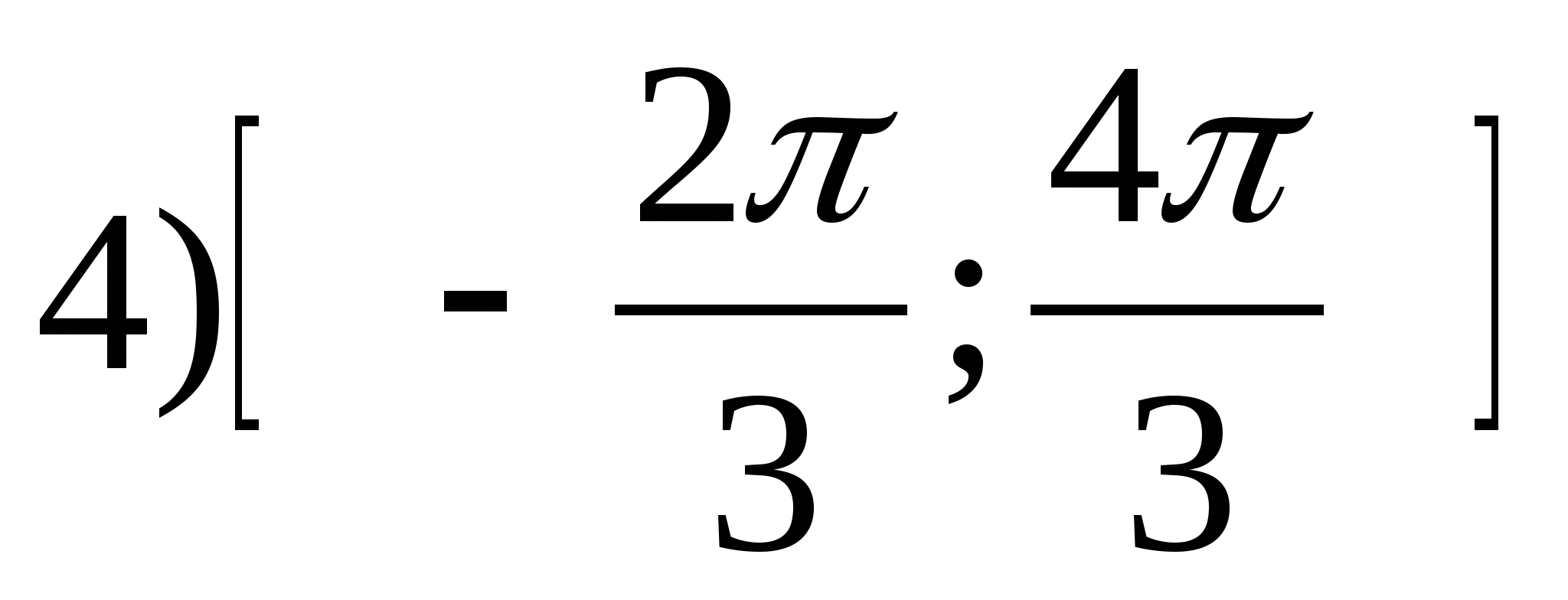
2. Намерете най-голямото цяло число на функцията

1) 4 2) 5 3) 6 4) 7

3. Кое от следните числа може да бъде стойност на функцията

1) 0 2) 3 3) 6 4) 9

куравнението - к + грях(2 х-1) = 2 разрешими?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Намерете набора от стойности на функцията по \u003d -cos 2 3 х + 4.

1) 2) 3) 4)

6. Посочете най-малката стойност на функцията
между

2) -1 3) 0 4) 1

7. Намерете колко цели числа има в диапазона на функцията y = 12cos 3 х +5 грях 3 х.

1) 13 2) 27 3) 26 4) 14

Вариант 10

1. Намерете диапазона на функцията

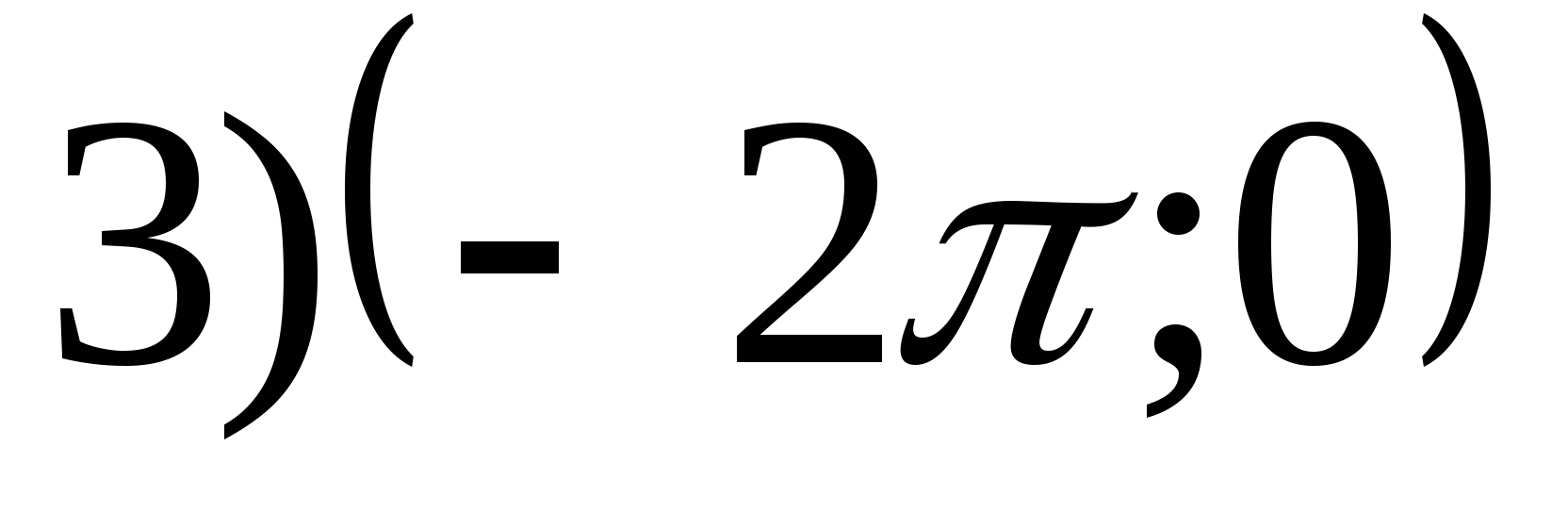
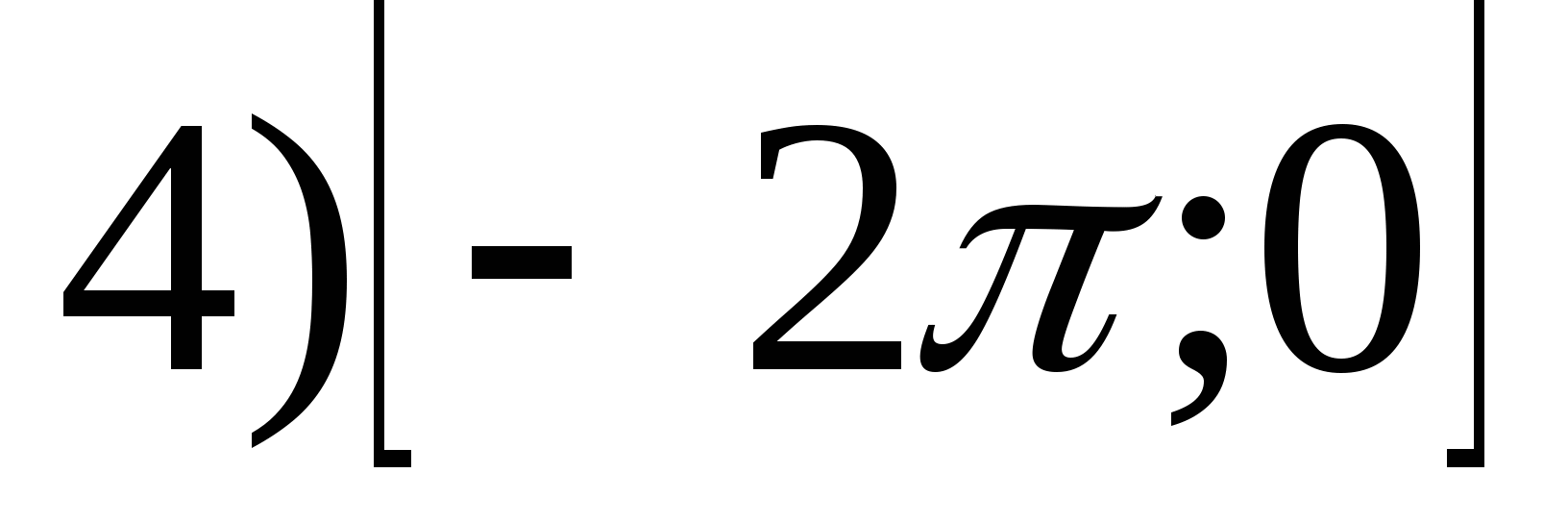
2. Намерете най-малката стойност на функцията

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Кое от следните числа може да бъде стойност на функцията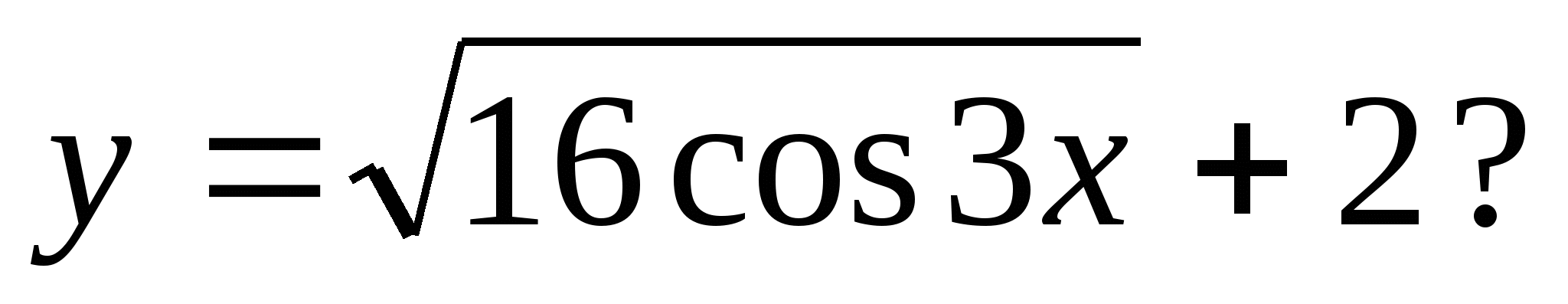

1) -4 2) -1 3) 3 4) 7

4. При какви стойности на параметърамуравнението cos (3 х + 2)- м= 5 има корени?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Намерете набора от стойности на функцията по \u003d -2ctg 2 3 х + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Посочете най-голямата стойност на функцията
между

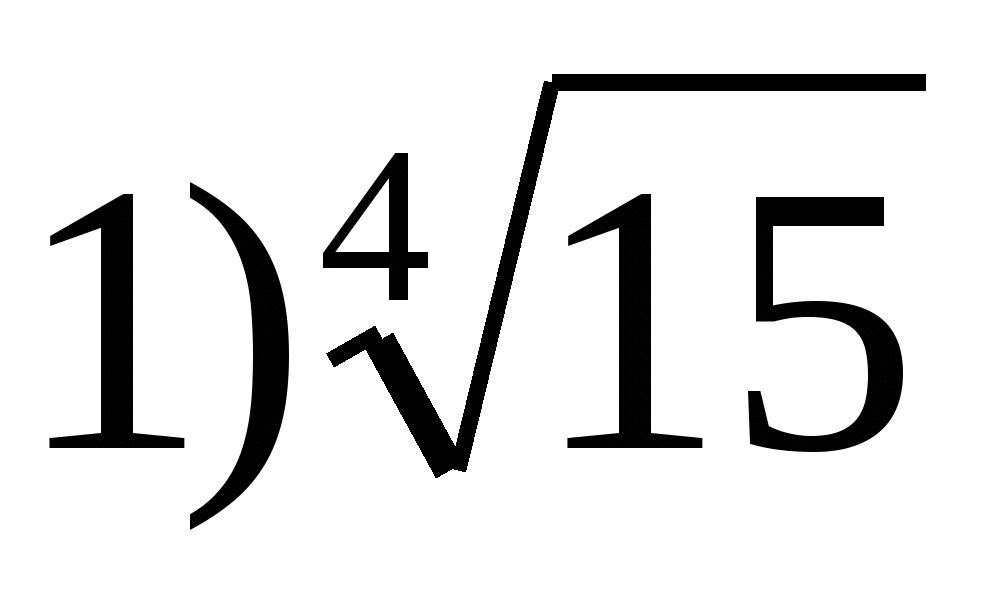2) 0 3) 2 4) 1

7. Намерете колко цели числа има в диапазона на функцията

1) 30 2) 35 3) 17 4) 7

Набор от стойности на експоненциални и логаритмични функции

Опция 1

1. Намерете диапазона на функцията

1) 4) (-∞;3)

2. Задайте набор от функционални стойности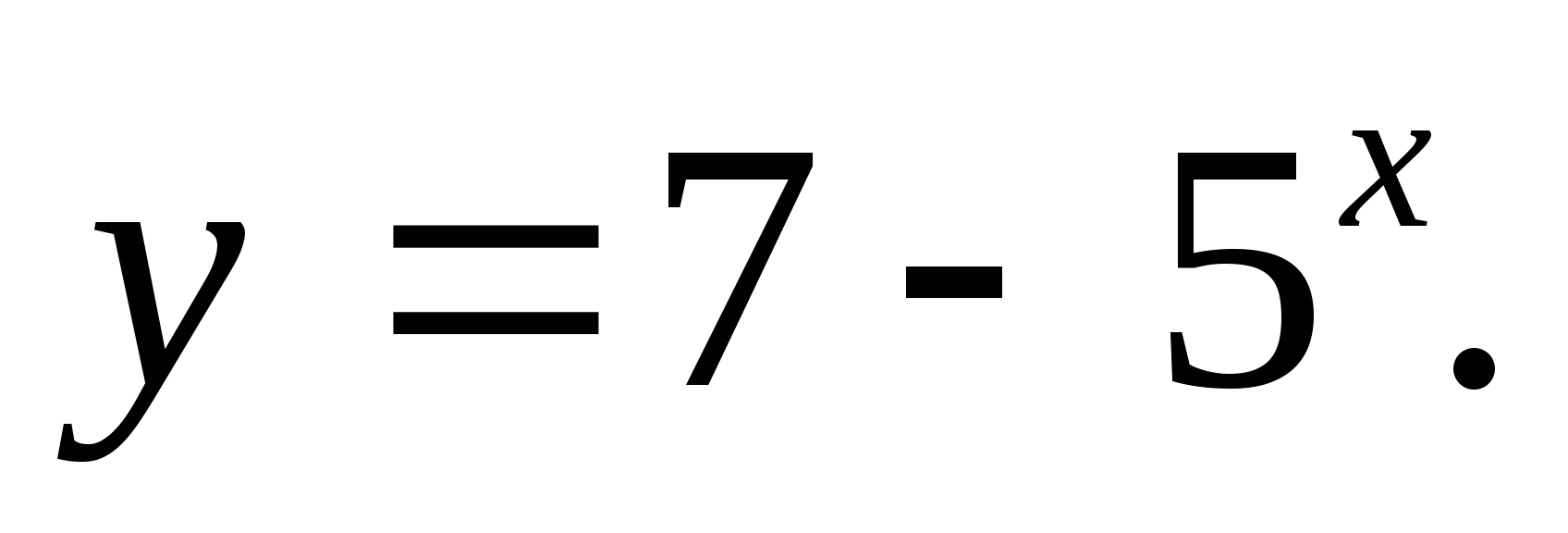

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Посочете най-малкото цяло число на функцията

1) 1 2) -1 3) 0 4) -5

7. Посочете функция, чийто набор от стойности е интервалът (1;∞).

Вариант 2

1. Задайте набор от функционални стойности

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Намерете диапазона на функцията

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Посочете най-малкото цяло число на функцията

1) -12 2) -11 3) -10 4) -15

4. Посочете число, което не принадлежи към набора от стойности на функцията

1) -42 2) 3 3) 1 4) -20

5. Задайте набор от функционални стойности

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Посочете най-голямото цяло число на функцията

1) 10 2) 3 3) 9 4) 2

7. Посочете функция, чийто набор от стойности е интервалът

(-∞;13).

Вариант 5

1. Посочете най-малкото цяло число на функцията

1) 0 2) -1 3) -2 4) -3

2. Кое от следните числа е в диапазона на функцията

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Намерете на кой сегмент е функцията
приема най-голямата стойност от 2 и най-малката стойност от -3.

1) 2) (-5;2) 3) 4) (-3;2)

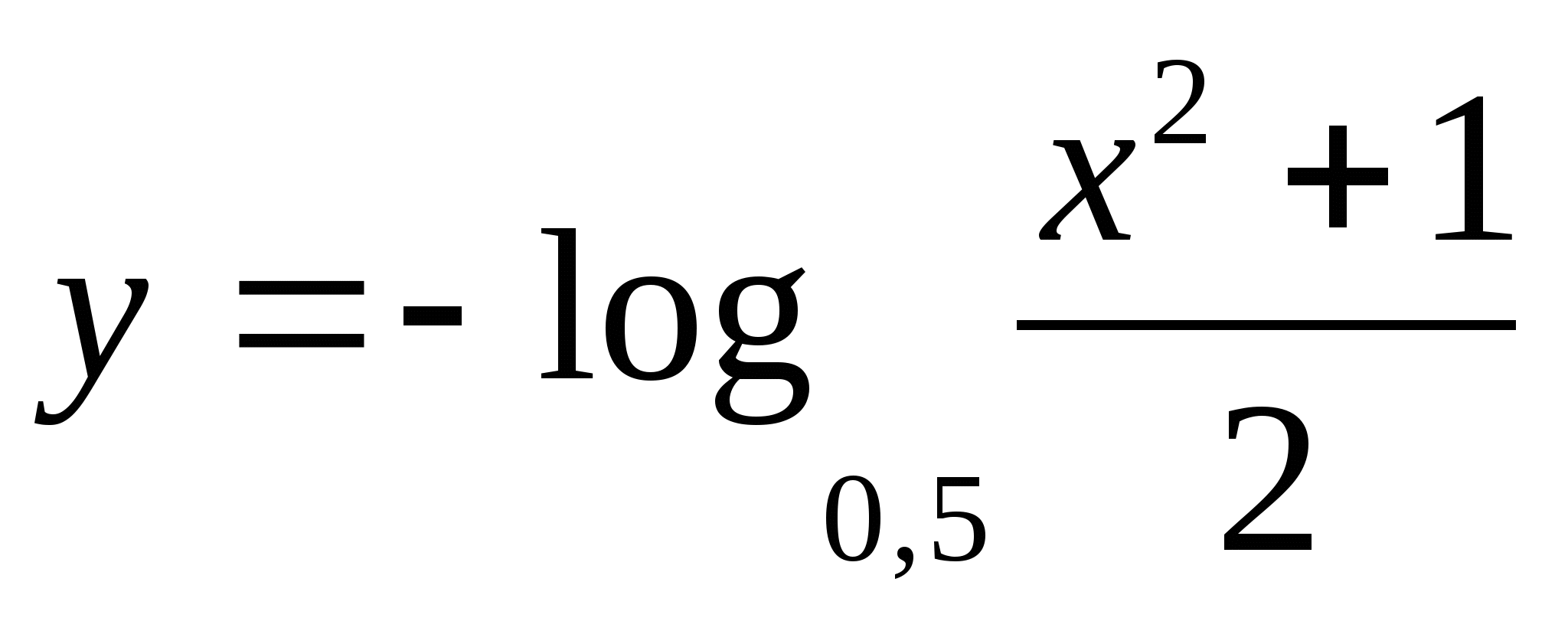между

1) -1/2 2) 5 3) 2 4) 4

8. Намерете сумата на всички естествени числа, които не са включени в множествата от стойности на функцията

1) 3 2) 6 3) 10 4) 8

Вариант 6

1. Посочете най-голямото цяло число на функцията

1) 2 2) 4 3) 3 4) 5

2. Кое от следните числа не е в диапазона на функцията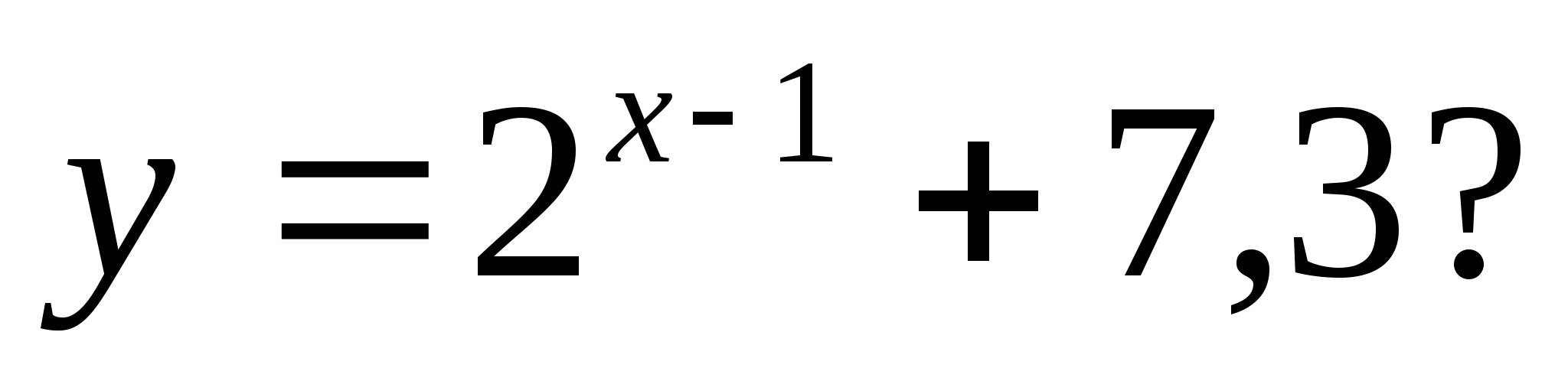

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Задайте набор от функционални стойности

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Намерете всички точки на ОУ, които са проекции на точките от графиката на функцията

1) (0;∞) 2) 2) (-3;2) 3) [ дневник 2 3;2] 4) (дневник 2 3;2)

6. Намерете на кой сегмент е функцията
приема най-малката стойност като -2 и най-голямата стойност като 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Посочете най-голямата стойност на функцията
между

[-0,9; 0]. 2. Намерете най-малката стойност на функцията върху отсечката.

4. Колко цели стойности приема функцията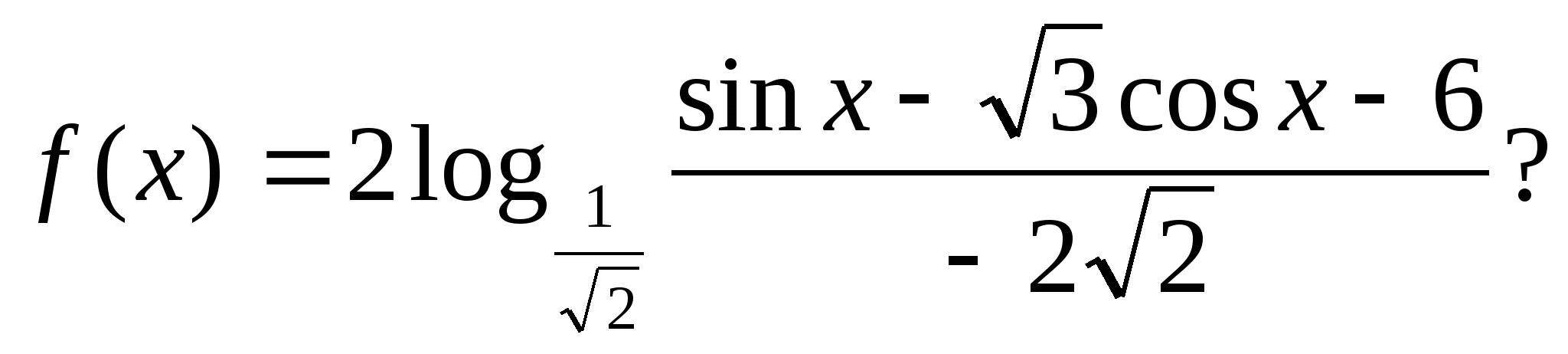

Отговори

Част 1

Набор от стойности на експоненциална и логаритмична функция

Част 2

Концепцията за функция и всичко свързано с нея е традиционно сложно, неразбрано напълно. Специален препъни камък при изучаването на функцията и подготовката за изпита е областта на дефиниция и диапазонът от стойности (промени) на функцията.
Често учениците не виждат разликата между областта на дадена функция и областта на нейните стойности.
И ако учениците успеят да овладеят задачите за намиране на областта на дефиниция на функция, тогава задачите за намиране на набор от стойности на функция им създават значителни трудности.
Целта на тази статия: запознаване с методите за намиране на стойностите на функция.
В резултат на разглеждането на тази тема беше изучен теоретичен материал, разгледани бяха методи за решаване на проблеми за намиране на набори от функционални стойности, избран дидактически материал за самостоятелна работа на студентите.
Статията може да се използва от учителя при подготовката на учениците за зрелостни и кандидатстудентски изпити, при изучаване на темата „Обхват на функция” във факултативните часове от избираемите дисциплини по математика.

I. Определяне на обхвата на функцията.

Площта (множество) от стойности E(y) на функцията y = f(x) е множеството от такива числа y 0, за всяко от които има такова число x 0, че: f(x 0) = y 0 .

Нека си припомним обхватите на основните елементарни функции.

Помислете за маса.

функция	Много ценности
y = kx + b	E(y) = (-∞;+∞)
y=x2n	E(y) =
y = cos x	E(y) = [-1;1]
y = tg x	E(y) = (-∞;+∞)
y = ctg x	E(y) = (-∞;+∞)
y = arcsin x	E(y) = [-π/2; π/2]
y = arcos x	E(y) =
y = арктан х	E(y) = (-π/2; π/2)
y = arcctg x	E(y) = (0; π)

Обърнете внимание също, че диапазонът на всеки полином от четна степен е интервалът, където n е най-голямата стойност на този полином.

II. Функционални свойства, използвани при намиране на диапазона на функция

За да се намери успешно множеството от стойности на функция, човек трябва да има добро познаване на свойствата на основните елементарни функции, особено техните области на дефиниране, диапазони от стойности и природата на монотонността. Нека представим свойствата на непрекъснати, монотонно диференцируеми функции, които най-често се използват при намиране на набор от стойности на функции.

Свойства 2 и 3 обикновено се използват заедно със свойството на елементарна функция да бъде непрекъсната в своята област. В този случай най-простото и най-кратко решение на проблема за намиране на набор от стойности на функция се постига въз основа на свойство 1, ако е възможно да се определи монотонността на функцията с помощта на прости методи. Решението на задачата е допълнително опростено, ако функцията освен това е четна или нечетна, периодична и т.н. По този начин, когато се решават задачи за намиране на набори от стойности на функцията, трябва да се проверят следните свойства на функцията и да се използват, ако е необходимо:

• непрекъснатост;
• монотонен;
• диференцируемост;
• четни, нечетни, периодични и др.

Простите задачи за намиране на набор от функционални стойности са предимно ориентирани:

а) използването на най-простите оценки и ограничения: (2 x > 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x? 1 и т.н.);

б) за да изберете пълен квадрат: x 2 - 4x + 7 \u003d (x - 2) 2 + 3;

в) за преобразуване на тригонометрични изрази: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

г) използвайки монотонността на функцията x 1/3 + 2 x-1 се увеличава с R.

III. Обмислете начини за намиране на обхватите на функциите.

а) последователно намиране на стойности на сложни функционални аргументи;
б) метод на оценка;
в) използване на свойствата на непрекъснатост и монотонност на функция;
г) използване на дериват;
д) използването на най-големите и най-малките стойности на функцията;
е) графичен метод;
ж) метод за въвеждане на параметър;
з) метод на обратната функция.

Ще разкрием същността на тези методи на конкретни примери.

Пример 1: Намерете диапазона E(y)функции y = log 0,5 (4 - 2 3 x - 9 x).

Нека решим този пример чрез последователно намиране на стойностите на аргументи на сложна функция. След като избрахме пълния квадрат под логаритъма, трансформираме функцията

y = log 0,5 (5 - (1 + 2 3 x - 3 2x)) = log 0,5 (5 - (3 x + 1) 2)

И последователно намерете наборите от стойности на неговите сложни аргументи:

E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)

Обозначете T= 5 – (3 x +1) 2 , където -∞≤ t≤4. По този начин проблемът се свежда до намиране на набора от стойности на функцията y = log 0,5 t на лъча (-∞;4) . Тъй като функцията y = log 0,5 t е дефинирана само при, тогава нейният набор от стойности на лъча (-∞;4) съвпада с набора от стойности на функцията на интервала (0;4), който е пресечната точка на лъча (-∞;4) с дефиниционната област (0;+∞) на логаритмичната функция. На интервала (0;4) тази функция е непрекъсната и намаляваща. При T> 0, тя клони към +∞ и когато t = 4 приема стойност -2, така че E(y) =(-2, +∞).

Пример 2: Намерете диапазона на функция

y = cos7x + 5cosx

Нека решим този пример чрез метода на оценките, чиято същност е да оценим непрекъснатата функция отдолу и отгоре и да докажем, че функцията достига долната и горната граница на оценките. В този случай съвпадението на набора от стойности на функцията с интервала от долната граница на оценката до горната се определя от непрекъснатостта на функцията и липсата на други стойности за нея.

От неравенствата -1≤cos7x?1, -5≤5cosx?5 получаваме оценката -6≤y?6. За x = p и x = 0 функцията приема стойностите -6 и 6, т.е. достига долната и горната граница. Като линейна комбинация от непрекъснати функции cos7x и cosx, функцията y е непрекъсната по цялата числова ос, следователно, чрез свойството на непрекъсната функция, тя приема всички стойности от -6 до 6 включително и само тях, тъй като , поради неравенствата -6≤y?6, други стойности тя е невъзможна. Следователно, E(y)= [-6;6].

Пример 3: Намерете диапазона E(f)функции f(x)= cos2x + 2cosx.

Използвайки формулата за двоен ъглов косинус, трансформираме функцията f(x)= 2cos 2 x + 2cosx – 1 и означ T= cosx. Тогава f(x)= 2t 2 + 2t – 1. Тъй като E(cosx) =

[-1;1], след това диапазонът на функцията f(x)съвпада с набора от стойности на функцията g (T)\u003d 2t 2 + 2t - 1 на сегмента [-1; 1], който ще намерим по графичен метод. След като начертахме функцията y = 2t 2 + 2t - 1 = 2(t + 0,5) 2 - 1,5 на интервала [-1; 1], намираме E(f) = [-1,5; 3].

Забележка – Много проблеми с параметър се свеждат до намиране на набор от стойности на функция, главно свързани с разрешимостта и броя решения на уравнението и неравенствата. Например уравнението f(x)= a е разрешимо тогава и само ако

aE(f)По същия начин уравнението f(x)= a има поне един корен, разположен на някакъв интервал X, или няма корен на този интервал, ако и само ако a принадлежи или не принадлежи към набора от стойности на функцията f(x)на интервала X. Ние също така изучаваме с помощта на набора от стойности на функцията и неравенствата f(x)≠а, f(x)>а и т.н. По-специално, f(x)≠и за всички допустими стойности на x, ако E(f)

Пример 4. За какви стойности на параметъра a уравнението (x + 5) 1/2 = a (x 2 + 4) има един корен в сегмента [-4;-1].

Нека напишем уравнението във формата (x + 5) 1/2 / (x 2 + 4) = a. Последното уравнение има поне един корен в сегмента [-4;-1] тогава и само ако a принадлежи към набора от стойности на функцията f(x) =(x + 5) 1/2 / (x 2 + 4) върху сегмента [-4;-1]. Нека намерим това множество, използвайки свойството за непрекъснатост и монотонност на функцията.

На отсечката [-4;-1] функцията y = xІ + 4 е непрекъсната, намаляваща и положителна, следователно функцията g(x) = 1/(x 2 + 4) е непрекъснат и нараства на този интервал, тъй като при разделяне на положителна функция естеството на монотонността на функцията се променя на обратното. функция h(x) =(x + 5) 1/2 е непрекъсната и растяща в своята област D(h) =[-5;+∞) и по-специално на интервала [-4;-1], където също е положителен. След това функцията f(x)=g(x) h(x), като продукт на две непрекъснати, нарастващи и положителни функции, също е непрекъснат и нараства на сегмента [-4;-1], следователно неговият набор от стойности на [-4;-1] е сегментът [ f(-4); f(-1)] = . Следователно уравнението има решение в интервала [-4;-1] и единственото (по свойството на непрекъсната монотонна функция) за 0,05 ≤ a ≤ 0,4

Коментирайте. Разрешимост на уравнението f(x) = aна някакъв интервал X е еквивалентно на принадлежност на стойностите на параметъра анабор от функционални стойности f(x)на X. Следователно наборът от стойности на функцията f(x)на интервала X съвпада с множеството стойности на параметрите а, за което уравнението f(x) = aима поне един корен в интервала X. По-специално диапазонът от стойности E(f)функции f(x)съответства на набора от стойности на параметрите а, за което уравнението f(x) = aима поне един корен.

Пример 5: Намерете диапазона E(f)функции

Нека решим примера, като въведем параметър, според който E(f)съответства на набора от стойности на параметрите а, за което уравнението

има поне един корен.

Когато a=2, уравнението е линейно - 4x - 5 = 0 с различен от нула коефициент за неизвестно x, следователно има решение. За a≠2 уравнението е квадратно, така че е разрешимо тогава и само ако неговият дискриминант

Тъй като точката a = 2 принадлежи на отсечката

след това желания набор от стойности на параметри а,следователно диапазонът от стойности E(f)ще бъде целият сегмент.

Като пряко развитие на метода за въвеждане на параметър при намиране на набор от стойности на функция, можем да разгледаме метода на обратната функция, за намирането на който е необходимо да се реши уравнението за x f(x)=y, като се има предвид y като параметър. Ако това уравнение има единствено решение x=g(y), след това обхвата E(f)оригинална функция f(x)съвпада с областта на дефиницията D(g)обратна функция g(y). Ако уравнението f(x)=yима множество решения x = g 1 (y), x \u003d g 2 (y)и т.н., тогава E(f)е равно на обединението на обхватите на дефинициите на функцията g 1 (y), g 2 (y)и т.н.

Пример 6: Намерете диапазона E(y)функции y = 5 2/(1-3x).

От уравнението

намерете обратната функция x = log 3 ((log 5 y – 2)/(log 5 y)) и нейната област D(x):

Тъй като уравнението за x има единствено решение, тогава

E(y) = D(x) = (0; 1)(25;+∞).

Ако домейнът на функция се състои от няколко интервала или функцията на различни интервали е дадена с различни формули, тогава за да намерите домейна на функцията, трябва да намерите наборите от стойности на функцията на всеки интервал и да вземете техните съюз.

Пример 7: Намиране на диапазони f(x)и f(f(x)), където

f(x)върху лъча (-∞;1], където съвпада с израза 4 x + 9 4 -x + 3. Означим t = 4 х. Тогава f(x) = t + 9/t + 3, където 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x)на лъча (-∞;1] съвпада с набора от стойности на функцията g(t) = t + 9/t + 3, на интервала (0;4], който намираме с помощта на производната g'(t) \u003d 1 - 9 / t 2. На интервала (0;4] производната g'(t)е дефинирано и изчезва там при t=3. На 0<T<3 она отрицательна, а при 3<T<4 положительна. Следовательно, в интервале (0;3) функция g(t)намалява, а в интервала (3;4) нараства, оставайки непрекъснат на целия интервал (0;4), така че g (3)= 9 - най-малката стойност на тази функция в интервала (0; 4], докато най-голямата й стойност не съществува, така че когато t→0дясна функция g(t)→+∞.След това, чрез свойството на непрекъсната функция, наборът от стойности на функцията g(t)върху интервала (0;4], а оттам и множеството от стойности f(x)на (-∞;-1], ще има лъч.

Сега, чрез комбиниране на интервалите - наборите от стойности на функцията f(f(x)), означават t = f(x). Тогава f(f(x)) = f(t), където Tфункция f(t)= 2cos( х-1) 1/2+ 7 и отново приема всички стойности от 5 до 9 включително, т.е. диапазон E(fІ) = E(f(f(x))) =.

По същия начин, обозначавайки z = f(f(x)), можете да намерите диапазона E(f3)функции f(f(f(x))) = f(z), където 5 ≤ z ≤ 9 и т.н. Уверете се, че E(f 3) = .

Най-универсалният метод за намиране на набора от стойности на функцията е да се използват най-големите и най-малките стойности на функцията в даден интервал.

Пример 8. За какви стойности на параметъра Рнеравенство 8 x - p ≠ 2x+1 – 2xважи за всички -1 ≤ x< 2.

Обозначаване t = 2 х, записваме неравенството като p ≠ t 3 - 2t 2 + t. защото t = 2 хе непрекъснато нарастваща функция на R,тогава за -1 ≤ x< 2 переменная

2 -1 ≤ t<2 2 ↔

0,5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда Рразлични от функционалните стойности f(t) \u003d t 3 - 2t 2 + tпри 0,5 ≤ t< 4.

Нека първо намерим набора от стойности на функцията f(t)на интервала, където има производна навсякъде f'(t) = 3t 2 - 4t + 1. Следователно, f(t)е диференцируема и следователно непрекъсната на сегмента . От уравнението f'(t) = 0намерете критичните точки на функцията t=1/3, t=1,първото от които не принадлежи на сегмента , а второто принадлежи на него. защото f(0,5) = 1/8, f(1) = 0, f(4) = 36,тогава, по свойството на диференцируема функция, 0 е най-малката, а 36 е най-голямата стойност на функцията f(t)на сегмента. Тогава f(t),като непрекъсната функция приема на сегмента всички стойности от 0 до 36 включително, а стойността 36 приема само когато t=4, така че за 0,5 ≤ t< 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Нека вземем задача, при която е необходимо да се определи диапазонът от стойности на арксинуса.

Пример 1

Състояние:намерете обхвата y = a r c sin x .

Решение

В общия случай областта на дефиниране на арксинуса се намира на интервала [ - 1 ; един ] . Трябва да определим най-голямата и най-малката стойност на посочената функция върху него.

y "= a r c sin x" = 1 1 - x 2

Знаем, че производната на функцията ще бъде положителна за всички x стойности, разположени в интервала [ - 1 ; 1 ], тоест в цялата област на дефиниция функцията арксинус ще нараства. Това означава, че той ще приеме най-малката стойност, когато x е равно на - 1, а най-голямата - когато x е равно на 1.

m i n x ∈ - 1; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2

Така диапазонът на функцията арксинус ще бъде равен на E (a r c sin x) = - π 2 ; π 2 .

Отговор: E (a r c sin x) \u003d - π 2; π 2

Пример 2

Състояние:изчислете обхвата y = x 4 - 5 x 3 + 6 x 2 върху дадения сегмент [ 1 ; четири ] .

Решение

Всичко, което трябва да направим, е да изчислим най-голямата и най-малката стойност на функцията в дадения интервал.

За да се определят екстремните точки, е необходимо да се извършат следните изчисления:

y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 и l и 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1 ;4 ;x3 = 15 + 338 ≈ 2,59 ∈ 1;4

Сега нека намерим стойностите на дадената функция в краищата на сегмента и точките x 2 = 15 - 33 8 ; x 3 \u003d 15 + 33 8:

y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2 . 08 y 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 y (4) = 4 4 - 5 4 3 + 6 4 2 = 32

Това означава, че наборът от функционални стойности ще се определя от сегмента 117 - 165 33 512 ; 32 .

Отговор: 117 - 165 33 512 ; 32 .

Нека да преминем към намиране на множеството от стойности на непрекъснатата функция y = f (x) в интервалите (a; b) и a; + ∞ , - ∞ ; b, -∞; +∞.

Нека започнем с определяне на най-големите и най-малките точки, както и интервалите на нарастване и намаляване в даден интервал. След това ще трябва да изчислим едностранни граници в краищата на интервала и/или граници в безкрайност. С други думи, трябва да определим поведението на функцията при дадени условия. За това имаме всички необходими данни.

Пример 3

Състояние:изчислете диапазона на функцията y = 1 x 2 - 4 на интервала (- 2 ; 2) .

Решение

Определете най-голямата и най-малката стойност на функцията за даден интервал

y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2)

Получихме максималната стойност, равна на 0, тъй като в този момент знакът на функцията се променя и графиката започва да намалява. Вижте илюстрацията:

Тоест y (0) = 1 0 2 - 4 = - 1 4 ще бъде максималната стойност на функцията.

Сега нека дефинираме поведението на функцията за x, която клони към - 2 от дясната страна и + 2 от лявата страна. С други думи, намираме едностранни ограничения:

lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞

Разбрахме, че стойностите на функцията ще се увеличат от минус безкрайност до - 1 4, когато аргументът се промени от - 2 на 0 . И когато аргументът се промени от 0 на 2, стойностите на функцията намаляват към минус безкрайност. Следователно наборът от стойности на дадената функция на интервала, от който се нуждаем, ще бъде (- ∞ ; - 1 4 ] .

Отговор: (- ∞ ; - 1 4 ] .

Пример 4

Състояние: посочете набора от стойности y = t g x на дадения интервал - π 2 ; π 2 .

Решение

Знаем, че като цяло производната на тангенса в - π 2; π 2 ще бъде положително, тоест функцията ще нараства. Сега нека дефинираме как се държи функцията в дадените граници:

lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

Получихме увеличение на стойностите на функцията от минус безкрайност до плюс безкрайност, когато аргументът се промени от - π 2 на π 2, и можем да кажем, че множеството от решения на тази функция ще бъде множеството от всички реални числа.

Отговор: - ∞ ; + ∞ .

Пример 5

Състояние:определете какъв е диапазонът на функцията натурален логаритъм y = ln x .

Решение

Знаем, че тази функция е дефинирана за положителни стойности на аргумента D (y) = 0 ; +∞. Производната на дадения интервал ще бъде положителна: y " = ln x " = 1 x . Това означава, че функцията се увеличава върху него. След това трябва да дефинираме едностранна граница за случая, когато аргументът отива до 0 (от дясната страна) и когато x отива до безкрайност:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Открихме, че стойностите на функцията ще нарастват от минус безкрайност до плюс безкрайност, когато стойностите на x се променят от нула до плюс безкрайност. Това означава, че наборът от всички реални числа е обхватът на функцията натурален логаритъм.

Отговор:множеството от всички реални числа е обхватът на функцията натурален логаритъм.

Пример 6

Състояние:определете какъв е диапазонът на функцията y = 9 x 2 + 1 .

Решение

Тази функция е дефинирана при условие, че x е реално число. Нека изчислим най-големите и най-малките стойности на функцията, както и интервалите на нейното нарастване и намаляване:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

В резултат на това установихме, че тази функция ще намалява, ако x ≥ 0; нараства, ако x ≤ 0; има максимална точка y (0) = 9 0 2 + 1 = 9, когато променливата е 0 .

Нека да видим как се държи функцията в безкрайност:

lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0

От записа може да се види, че стойностите на функцията в този случай асимптотично ще се доближат до 0.

За да обобщим: когато аргументът се промени от минус безкрайност до нула, тогава стойностите на функцията нарастват от 0 до 9. Тъй като стойностите на аргумента преминават от 0 до плюс безкрайност, съответните стойности на функцията ще намалеят от 9 на 0. Изобразили сме това на фигурата:

Това показва, че диапазонът на функцията ще бъде интервалът E (y) = (0 ; 9 ]

Отговор: E (y) = (0 ; 9 ]

Ако трябва да определим набора от стойности на функцията y = f (x) на интервалите [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , тогава ще трябва да извършим точно същите изследвания. Все още няма да анализираме тези случаи: ще ги срещнем по-късно в задачи .

Но какво ще стане, ако домейнът на определена функция е обединение на няколко интервала? След това трябва да изчислим наборите от стойности на всеки от тези интервали и да ги комбинираме.

Пример 7

Състояние:определете какъв ще бъде обхватът на y = x x - 2.

Решение

Тъй като знаменателят на функцията не трябва да се превръща в 0 , тогава D (y) = - ∞ ; 2 ∪ 2 ; +∞.

Нека започнем с дефиниране на набора от стойности на функцията на първия сегмент - ∞ ; 2, която е отворена греда. Знаем, че функцията върху нея ще намалява, тоест производната на тази функция ще бъде отрицателна.

lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Тогава, в случаите, когато аргументът се променя към минус безкрайност, стойностите на функцията асимптотично ще се доближат до 1. Ако стойностите на x се променят от минус безкрайност до 2, тогава стойностите ще намалеят от 1 до минус безкрайност, т.е. функцията на този сегмент ще приема стойности от интервала - ∞ ; един . Ние изключваме единството от нашите разсъждения, тъй като стойностите на функцията не го достигат, а само асимптотично се доближават до него.

За отворена греда 2 ; + ∞ извършваме абсолютно същите действия. Функцията върху него също намалява:

lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

Стойностите на функцията на този сегмент се определят от множеството 1 ; +∞. Това означава, че диапазонът от стойности на функцията, посочен в условието, от което се нуждаем, ще бъде обединението на множества - ∞; 1 и 1; +∞.

Отговор: E (y) = - ∞; 1 ∪ 1; +∞.

Това може да се види на графиката:

Специален случай са периодичните функции. Тяхната област на стойност съвпада с набора от стойности на интервала, който съответства на периода на тази функция.

Пример 8

Състояние:определете диапазона на синус y = sin x .

Решение

Синус се отнася за периодична функция и нейният период е 2 пи. Взимаме отсечка 0 ; 2 π и вижте какъв ще бъде наборът от стойности върху него.

y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

В рамките на 0; 2 π функцията ще има крайни точки π 2 и x = 3 π 2 . Нека изчислим на какво ще бъдат равни стойностите на функцията в тях, както и на границите на сегмента, след което избираме най-голямата и най-малката стойност.

y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1 , max x ∈ 0 ; 2 π sinx \u003d sin π 2 \u003d 1

Отговор: E (sinx) = - 1; един .

Ако трябва да знаете обхватите на функции като експоненциална, експоненциална, логаритмична, тригонометрична, обратна тригонометрична, тогава ви съветваме да прочетете отново статията за основните елементарни функции. Теорията, която представяме тук, ни позволява да тестваме посочените там стойности. Желателно е да ги научите, тъй като често се изискват при решаване на проблеми. Ако знаете обхватите на основните функции, тогава можете лесно да намерите обхватите на функциите, които се получават от елементарни с помощта на геометрична трансформация.

Пример 9

Състояние:определете обхвата y = 3 a r c cos x 3 + 5 π 7 - 4 .

Решение

Знаем, че сегментът от 0 до пи е диапазонът на арккосинуса. С други думи, E (a r c cos x) = 0; π или 0 ≤ a r c cos x ≤ π. Можем да получим функцията a r c cos x 3 + 5 π 7 от арккосинуса, като го преместим и разтегнем по оста O x, но такива трансформации няма да ни дадат нищо. Следователно, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .

Функцията 3 a r c cos x 3 + 5 π 7 може да се получи от обратния косинус a r c cos x 3 + 5 π 7 чрез разтягане по оста y, т.е. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Крайната трансформация е изместване по оста O y с 4 стойности. В резултат на това получаваме двойно неравенство:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4

Разбрахме, че диапазонът, от който се нуждаем, ще бъде равен на E (y) = - 4 ; 3 пи - 4 .

Отговор: E (y) = - 4; 3 пи - 4 .

Нека напишем още един пример без обяснения, т.к той е напълно подобен на предишния.

Пример 10

Състояние:изчислете какъв ще бъде диапазонът на функцията y = 2 2 x - 1 + 3 .

Решение

Нека пренапишем функцията, дадена в условието като y = 2 · (2 ​​​​x - 1) - 1 2 + 3 . За степенна функция y = x - 1 2 диапазонът ще бъде определен на интервала 0 ; + ∞ , т.е. x - 1 2 > 0 . В такъв случай:

2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3

Така че E (y) = 3; +∞.

Отговор: E (y) = 3; +∞.

Сега нека да разгледаме как да намерим диапазона на функция, която не е непрекъсната. За да направим това, трябва да разделим цялата област на интервали и да намерим наборите от стойности на всеки от тях и след това да комбинираме това, което имаме. За да разберете по-добре това, ви съветваме да прегледате основните типове точки на прекъсване на функцията.

Пример 11

Състояние:дадена функция y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3 . Изчислете обхвата му.

Решение

Тази функция е дефинирана за всички x стойности. Нека го анализираме за приемственост със стойностите на аргумента, равни на - 3 и 3:

lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)

Имаме невъзстановима прекъснатост от първи род със стойност на аргумента - 3 . Когато се приближите до нея, стойностите на функцията клонят към - 2 sin 3 2 - 4 , а когато x клони към - 3 от дясната страна, стойностите ще клонят към - 1 .

lim x → 3 - 0 f(x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f(x) = lim x → 3 + 0 1 x - 3 = + ∞

Имаме неотстраним прекъсване от втори род в точка 3. Когато функцията се стреми към нея, нейните стойности се приближават до - 1, докато се стремят към същата точка вдясно - до минус безкрайност.

Това означава, че цялата област на дефиниране на тази функция е разделена на 3 интервала (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .

На първия от тях получихме функцията y \u003d 2 sin x 2 - 4. Тъй като - 1 ≤ sin x ≤ 1, получаваме:

1 ≤ sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

Това означава, че на този интервал (- ∞ ; - 3 ] множеството от стойности на функцията е [ - 6 ; 2 ] .

На полуинтервала (- 3 ; 3 ] получаваме постоянна функция y = - 1 . Следователно целият набор от нейните стойности в този случай ще бъде намален до едно число - 1 .

На втория интервал 3 ; + ∞ имаме функция y = 1 x - 3 . Намалява, защото y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Следователно наборът от стойности на оригиналната функция за x > 3 е наборът 0 ; +∞. Сега нека комбинираме резултатите: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; +∞.

Отговор: E (y) = - 6; - 2 ∪ - 1 ∪ 0 ; +∞.

Решението е показано на графиката:

Пример 12

Условие: има функция y = x 2 - 3 e x . Определете множеството от неговите стойности.

Решение

Дефинира се за всички стойности на аргументи, които са реални числа. Нека определим в какви интервали тази функция ще нараства и в кои ще намалява:

y "= x 2 - 3 e x" = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

Знаем, че производната ще стане 0, ако x = - 1 и x = 3. Поставяме тези две точки на оста и откриваме какви знаци ще има производната на получените интервали.

Функцията ще намалява с (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) и ще нараства с [ - 1 ; 3]. Минималната точка ще бъде - 1 , максималната - 3 .

Сега нека намерим съответните стойности на функцията:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

Нека да разгледаме поведението на функцията в безкрайност:

lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 "e x" = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x "(e x)" = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0

За изчисляване на втората граница е използвано правилото на L'Hopital. Нека начертаем нашето решение на графика.

Той показва, че стойностите на функцията ще намалеят от плюс безкрайност до -2 e, когато аргументът се промени от минус безкрайност до -1. Ако се промени от 3 до плюс безкрайност, тогава стойностите ще намалеят от 6 e - 3 до 0, но 0 няма да бъде достигната.

Така E (y) = [ - 2 e ; +∞).

Отговор: E (y) = [ - 2 e ; +∞)

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter