D(f)- tie hodnoty, ktoré môže nadobudnúť argument, t.j. rozsah funkcie.

E(f)- tie hodnoty, ktoré funkcia môže nadobudnúť, t.j. súbor funkčných hodnôt.

Metódy hľadania rozsahov funkcií.

postupné zisťovanie hodnôt argumentov zložitých funkcií;

bodovacia/hraničná metóda;

využitie vlastností spojitosti a monotónnosti funkcie;

použitie derivátu;

použitie najväčších a najmenších hodnôt funkcie;

grafická metóda;

metóda zavádzania parametrov;

metóda inverznej funkcie.

Uvažujme o niektorých z nich.

Použitie derivátu

Všeobecný prístup nájsť množinu hodnôt spojitej funkcie f(x) znamená nájsť najväčšiu a najmenšiu hodnotu funkcie f(x) v jej doméne (alebo dokázať, že jedna alebo obe neexistujú) .

Ak potrebujete nájsť množinu hodnôt funkcie na segmente:

nájdite deriváciu danej funkcie f "(x);

nájdite kritické body funkcie f(x) a vyberte tie, ktoré patria do daného segmentu;

vypočítajte hodnoty funkcie na koncoch segmentu a vo vybraných kritických bodoch;

spomedzi nájdených hodnôt vyberte najmenšiu a najväčšiu hodnotu;

Medzi týmito hodnotami sa uzatvára množina funkčných hodnôt.

Ak je rozsah funkcie interval, potom sa použije rovnaká schéma, ale namiesto hodnôt na koncoch sa použijú limity funkcie, keď argument smeruje ku koncom intervalu. Limitné hodnoty od nie sú zahrnuté v súbore hodnôt.

Hraničná/bodová metóda

Ak chcete nájsť množinu hodnôt funkcií, najskôr nájdite množinu hodnôt argumentov a potom nájdite zodpovedajúce minimálne a maximálne hodnoty funkcie funkcie. Pomocou nerovností – určiť hranice.

Podstatou je odhadnúť spojitú funkciu zdola a zhora a dokázať, že funkcia dosahuje dolnú a hornú hranicu odhadov. V tomto prípade je zhoda množiny hodnôt funkcie s intervalom od dolnej hranice odhadu po hornú určená kontinuitou funkcie a absenciou iných hodnôt.

Vlastnosti spojitej funkcie

Ďalšou možnosťou je transformovať funkciu na spojitú monotónnu funkciu, následne pomocou vlastností nerovností odhadnúť množinu hodnôt novo získanej funkcie.

Postupné hľadanie hodnôt komplexných funkčných argumentov

Na základe postupného vyhľadávania množiny hodnôt medziľahlých funkcií, ktoré tvoria funkciu

Rozsahy základných elementárnych funkcií

Funkcia	Veľa hodnôt
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^(2n)$	E(y) =
$y = \cos(x)$	E(y) = [-1;1]
$y = (\rmtg)\, x$	E(y) = (-∞;+∞)
$y = (\rm ctg)\, x$	E(y) = (-∞;+∞)
$y = \arcsin(x)$	E(y) = [-π/2; π/2]
$y = \arccos(x)$	E(y) =
$y = (\rm arctg)\, x$	E(y) = (-π/2; π/2)
$y = (\rm arcctg)\, x$	E(y) = (0; π)

Príklady

Nájdite množinu funkčných hodnôt:

Použitie derivátu

Nájdite definičný obor: D(f)=[-3;3], pretože $9-x^(2)\geq 0$

Nájdite derivát: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0, ak x = 0. f"(x) neexistuje, ak $\sqrt(9-x^(2))=0$, t. j. pre x = ±3. Získame tri kritické body: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, z ktorých dva sa zhodujú s koncami segmentu. Vypočítajte: f(–3) = 0, f(0) = 3, f(3) = 0. Najmenšia hodnota f(x) je teda 0, najväčšia hodnota je 3.

Odpoveď: E(f) = .

NEPOUŽÍVAJTE derivát

Nájdite najväčšie a najmenšie hodnoty funkcie:

Od $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $, potom:

$f(x)\leq \frac(3)(4)$ pre všetky x;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ pre všetky x(pretože $|\cos (x)|\leq 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

Odpoveď: $\frac(3)(4)$ a $-\frac(3)(2)$

Ak tento problém vyriešite pomocou derivácií, potom budete musieť prekonať prekážky spojené s tým, že funkcia f (x) nie je definovaná na úsečke, ale na celej reálnej čiare.

Použitie metódy hraníc/odhadov

Z definície sínusu vyplýva, že $-1\leq\sin(x)\leq 1$. Ďalej použijeme vlastnosti číselných nerovností.

$-4\leq - 4\sin(x)\leq 4$, (vynásobte všetky tri časti dvojitej nerovnosti -4);

$1\leq 5 - 4\sin(x)\leq 9$ (pripočítané k trom častiam dvojitej nerovnosti 5);

Keďže táto funkcia je spojitá v celej oblasti definície, množina jej hodnôt leží medzi jej najmenšou a najväčšou hodnotou v celej oblasti definície, ak existuje.

V tomto prípade je množinou hodnôt funkcie $y = 5 - 4\sin(x)$ množina .

Z nerovností $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ získame odhad $$\\ -6\leq y\ leq 6 $ $

Pre x = p a x = 0 má funkcia hodnoty -6 a 6, t.j. dosahuje dolnú a hornú hranicu. Ako lineárna kombinácia spojitých funkcií cos(7x) a cos(x) je funkcia y spojitá pozdĺž celej číselnej osi, takže vlastnosťou spojitej funkcie nadobúda všetky hodnoty od -6 do 6 vrátane a iba oni, keďže kvôli nerovnostiam $- 6\leq y\leq 6$ iné hodnoty nie sú pre ňu možné.

Preto E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Odpoveď: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Transformujme výraz $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \vpravo) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.

Definícia kosínusu znamená $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

Keďže táto funkcia je spojitá na celej doméne definície, potom je množina jej hodnôt uzavretá medzi jej najmenšou a najväčšou hodnotou, ak existuje, množinou hodnôt funkcie $y =\sqrt(2)\ cos((x +\frac(\pi)(4)))$ je množina $[-\sqrt(2);\sqrt(2)]$.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

Označte $t = 5 – (3^(x)+1)^(2)$, kde -∞≤t≤4. Problém sa teda redukuje na nájdenie množiny hodnôt funkcie $y = \log_(0,5)(t)$ na lúči (-∞;4). Keďže funkcia $y = \log_(0,5)(t)$ je definovaná len pre t > 0 , jej množina hodnôt na lúči (-∞;4) sa zhoduje s množinou hodnôt funkcia na intervale (0;4), ktorá predstavuje priesečník lúča (-∞;4) s definičným oborom (0;+∞) logaritmickej funkcie. Na intervale (0;4) je táto funkcia spojitá a klesajúca. Pre t > 0 má tendenciu k +∞ a pre t = 4 nadobúda hodnotu -2, takže E(y) = (-2, +∞).

Používame techniku ​​založenú na grafickom znázornení funkcie.

Po transformáciách funkcie máme: y 2 + x 2 = 25 a y ≥ 0, |x| ≤ 5.

Treba pripomenúť, že $x^(2)+y^(2)=r^(2)$ je rovnica kruhu s polomerom r.

Pri týchto obmedzeniach je grafom tejto rovnice horný polkruh so stredom v počiatku a polomer rovný 5. Je zrejmé, že E(y) = .

Odpoveď: E(y) = .

Referencie

Rozsah funkcií v úlohách jednotnej štátnej skúšky, Minyuk Irina Borisovna

Tipy na nájdenie množiny funkčných hodnôt, Belyaeva I., Fedorova S.

Nájdenie množiny funkčných hodnôt

Ako riešiť problémy z matematiky na prijímacích skúškach, I.I. Melnikov, I.N. Sergeev

GBOU lýceum (hospodárske) s. Isakla

Učiteľka matematiky Kuzaeva V.N.

2016

Referenčné materiály

Ukážka riešenia Nájdite množinu funkčných hodnôt

Rozsah funkcie
je

r - ľubovoľné číslo

Rozsah funkcie
je r - ľubovoľné číslo

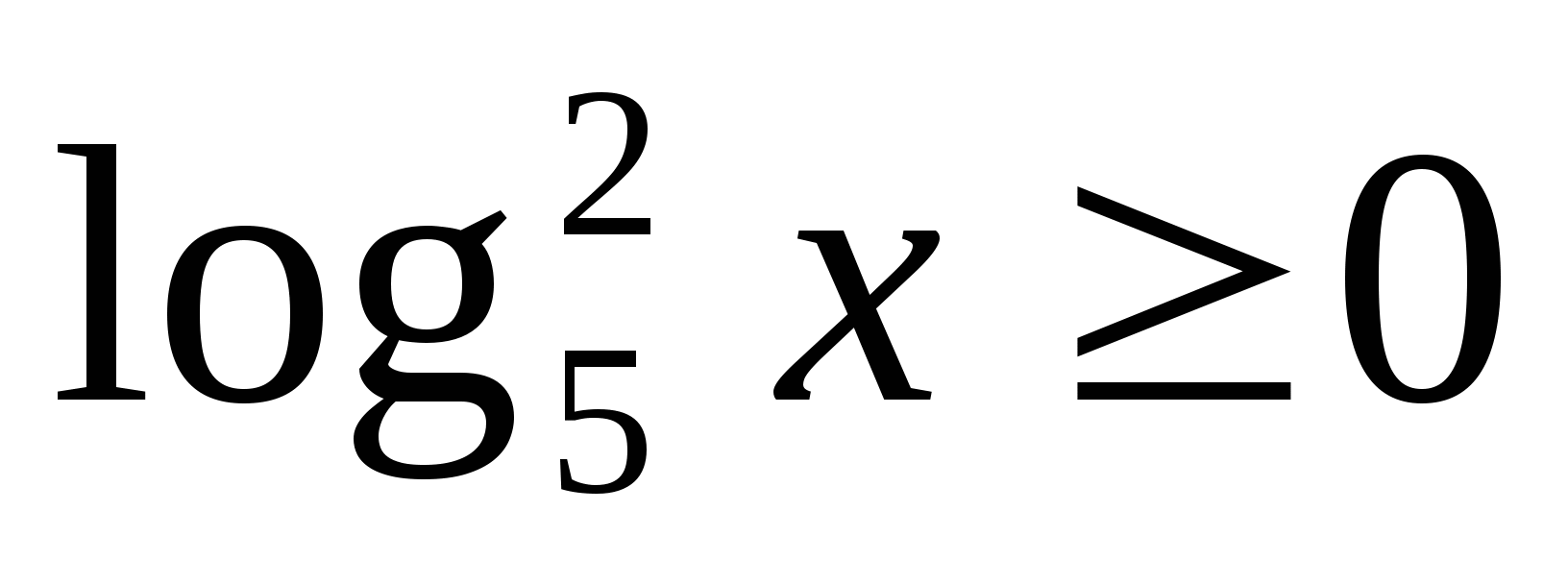
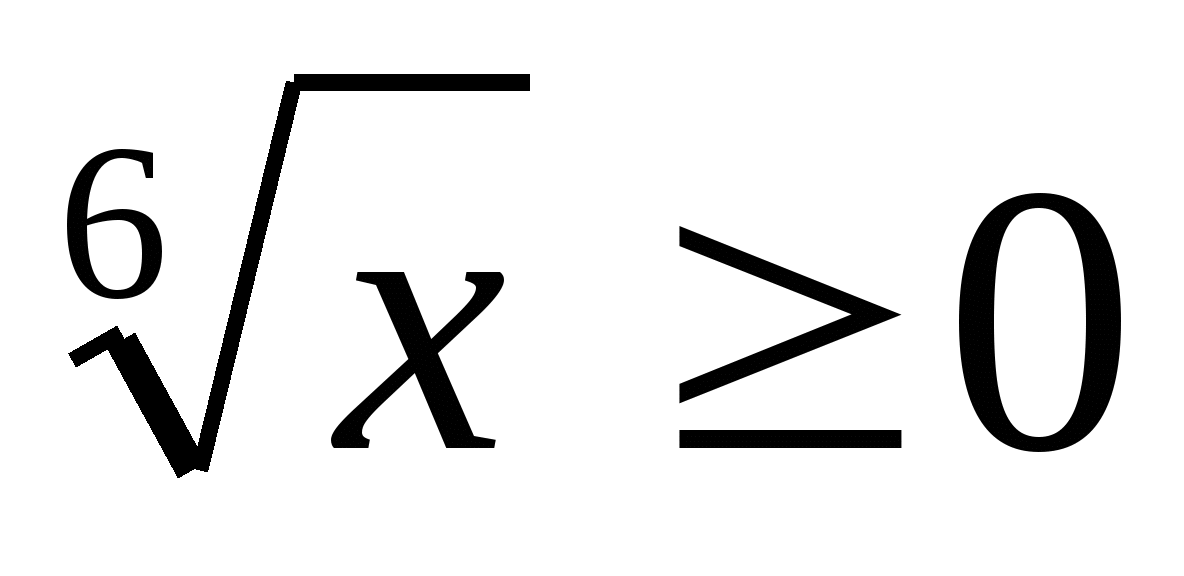
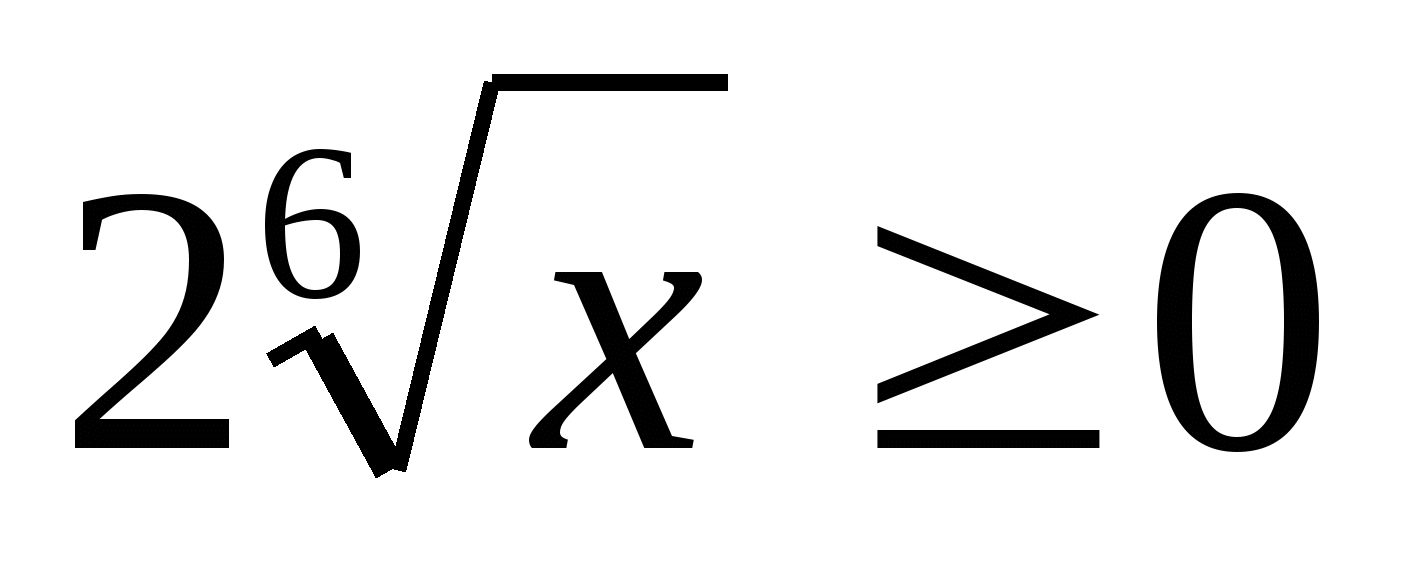
Veľa hodnôt

r - ľubovoľné číslo

Najvyššia hodnota

Najnižšia hodnota

doména X - ľubovoľné číslo
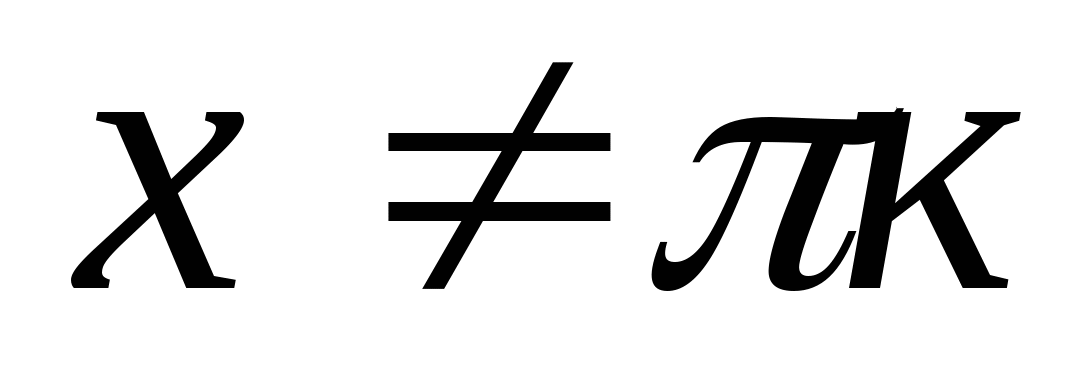, kde

, kde

Veľa hodnôt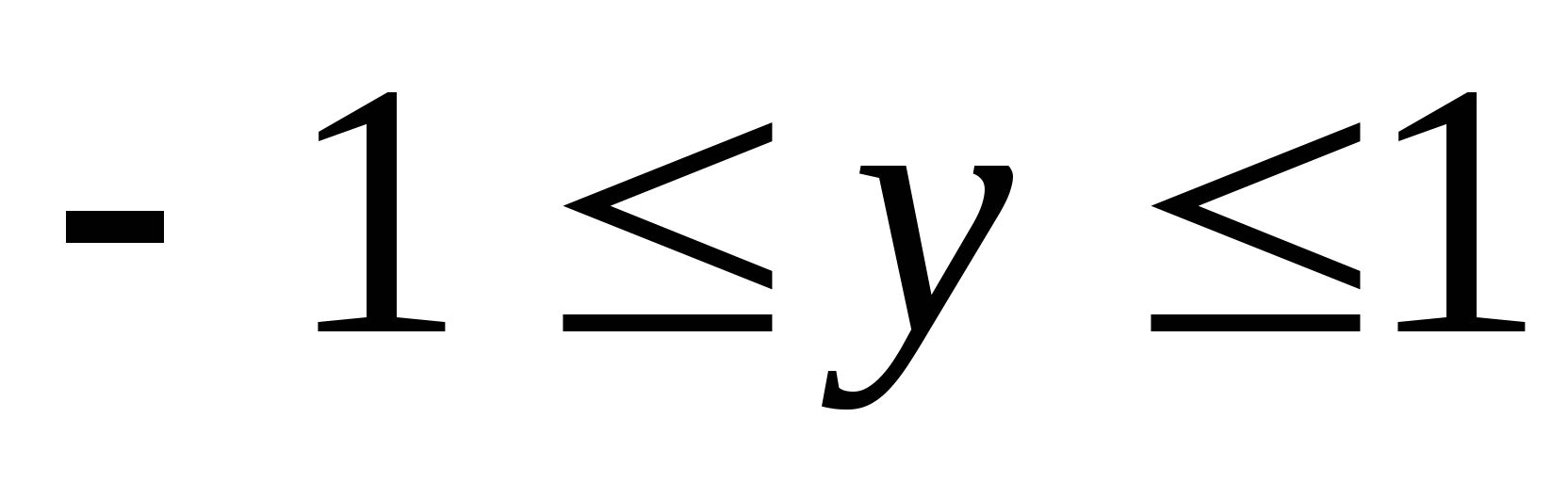
r - ľubovoľné číslor - ľubovoľné číslo

Vykresľovanie šablón pre niektoré goniometrické funkcie

Sada hodnôt goniometrických funkcií

možnosť 1

Y =hriech 3x+2.

1) (-5;5) 2) 3) 4) (1;5)

2. Nájdite oblasť funkcie y =tg x + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. Zadajte najmenšie celé číslo z rozsahu funkcie

y = 12,7 + 5 hriech(3x-2).

1) -5 2) 8 3) 5 4) 17

5. Zadajte funkciu, ktorej množinou hodnôt je segment [-2;2].

1) y = cos 2x 2) y = hriech 2 X 3) r = cos 2 X +2

4) r = 2 hriech 4 X

6. Nájdite množinu funkčných hodnôtr = tg 2 Xna segmente

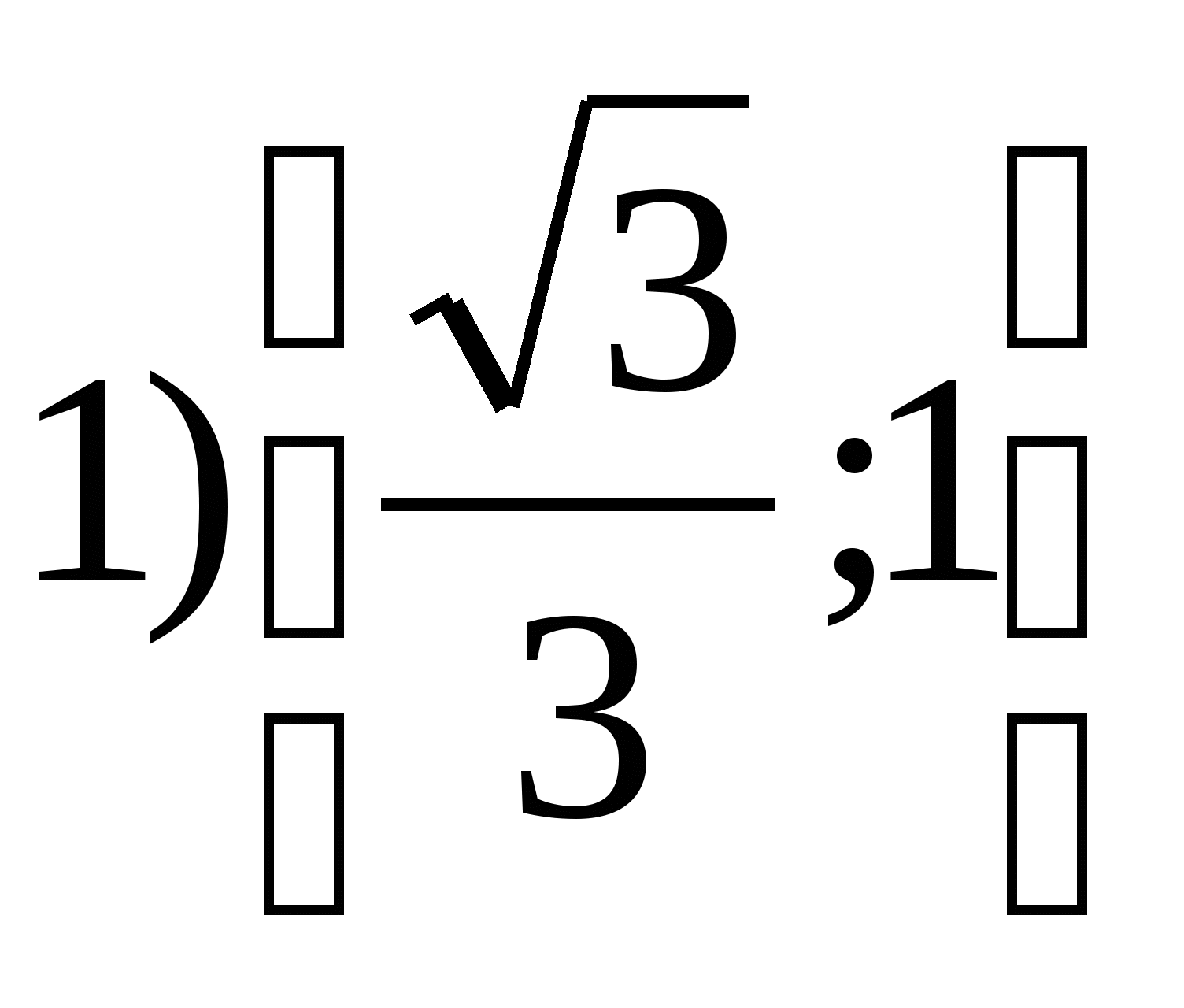
7. Nájdite súčet všetkých celých čísel, ktoré sú v rozsahu funkcier = 4 cos 2 X – 7.

1) -25 2) 25 3) -22 4) 0

Možnosť 2

r = 2 cos 5 X +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Nájdite rozsah funkcie

1) 3) (-∞;∞) 4) .

3. Zadajte najmenšie číslo z rozsahu funkcie

1) 4 2) -3 3) 1 4) -7

4. Zadajte najväčšie celé číslo z rozsahu funkcie

1) 2 2) 13 3) 12 4) -2

5. Zadajte funkciu, ktorej množinou hodnôt je segment [-5;5].

1) y = hriech 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = hriech 5x + 5

6. Nájdite množinu funkčných hodnôt
na segmente

7. Nájdite súčin všetkých celých čísel, ktoré sú v rozsahu funkcie y \u003d 5 – 3hriech 2 X.

1) 120 2) 14 3) -15 4) 0

Možnosť 3
1. Zadajte množinu funkčných hodnôtr = hriech 3 X + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Zadajte najmenšie číslo z rozsahu funkcie y = 5tg 2 X+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Zadajte funkciu, ktorej množinou hodnôt je segment

[-17;-13].

1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 sin x +10

6. Uveďte najmenšie prirodzené číslo, ktoré nie je zahrnuté v množine funkčných hodnôt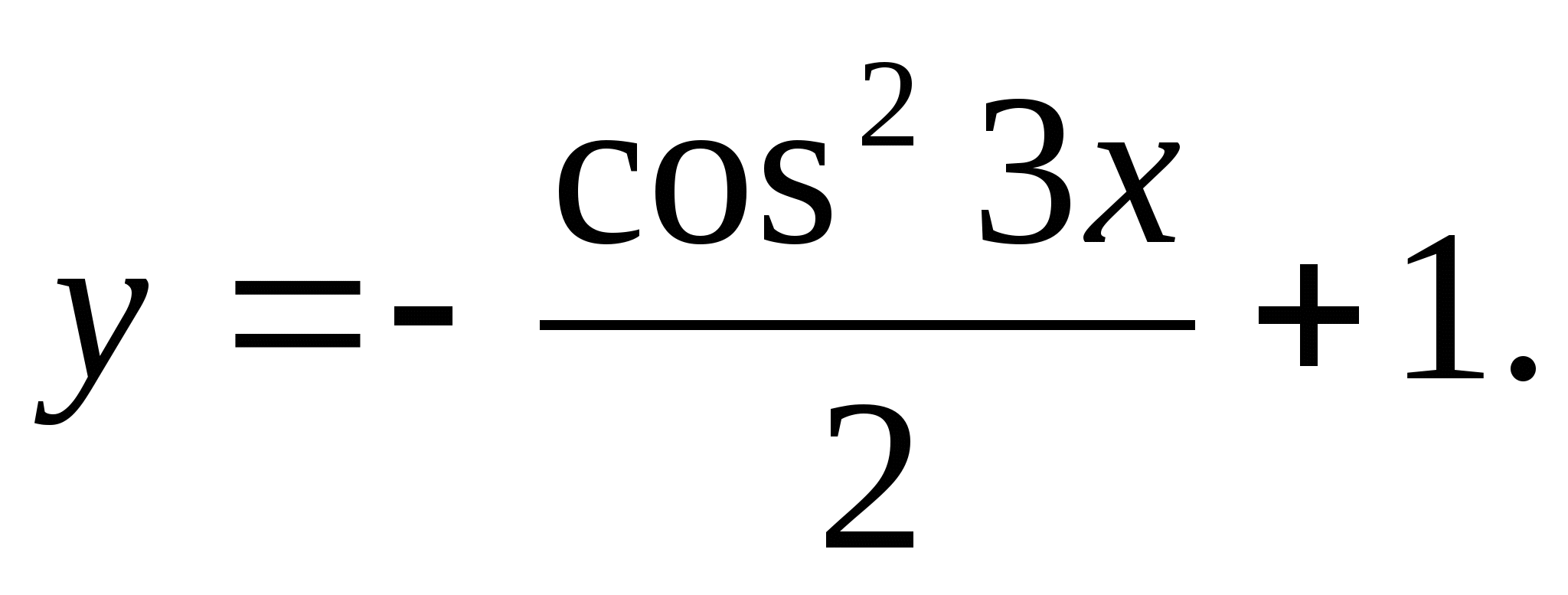

1) 2 2) 4 3) 15 4) 6

7. Koľko celých čísel patrí do množiny funkčných hodnôt

r = 2 cos 3 X +10?

1) 2 2) 3 3) 4 5) 5

Možnosť 4

1) 2) 4) (-7;-6)

2. Nájdite rozsah funkcie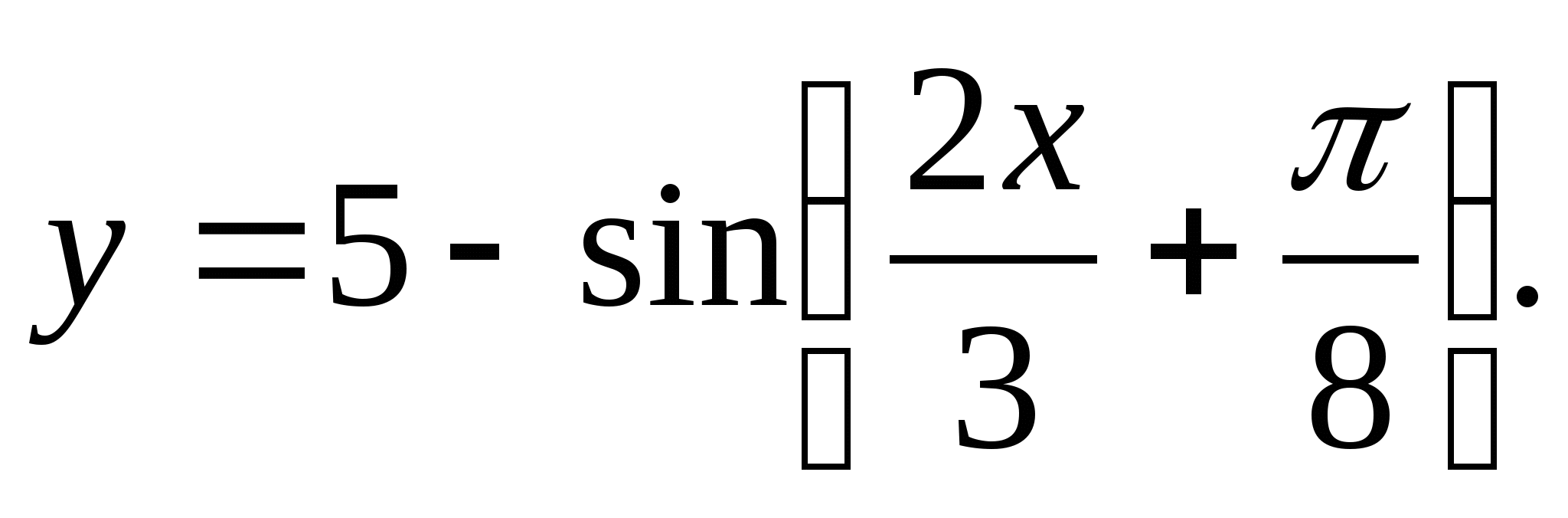

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Zadajte najväčšie číslo z rozsahu funkcier = -3 ctg 2 X+7.

1) 10 2) 4 3) 7 4) -3

4. Ktoré z nasledujúcich čísel nie je zahrnuté v množine funkčných hodnôt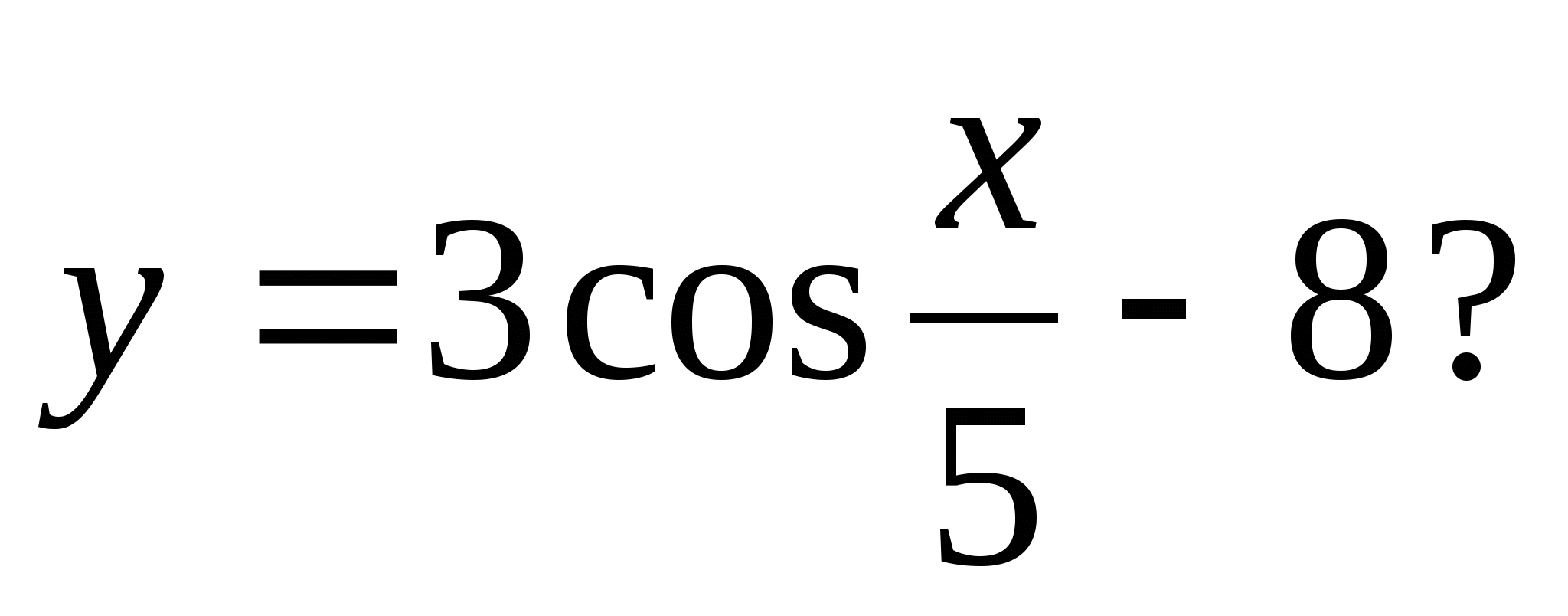

1) -6 2) -5 3) -10 4) -7

5. Zadajte funkciu, ktorej množinou hodnôt je interval .

6. Zadajte najväčšie záporné celé číslo, ktoré nie je zahrnuté v rozsahu funkcie

1) -1 2) -25 3) -6 4) -2

7. Koľko celých čísel patrí do množiny funkčných hodnôt

1) 11 2) 3 3) 5 4) 4

Možnosť 5

1. Zadajte množinu funkčných hodnôt y = 2 -hriech 5 X.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Nájdite rozsah funkcie

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Zadajte najmenšie celé číslo z rozsahu funkcie

r = 3 + hriech 2 2 X.

1) 0 2) 1 3) 3 4) 4

4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt

1) 128 2) 10,5 3) 3 4) -235

5. Zadajte funkciu, ktorej množinou hodnôt je segment [-9;15].

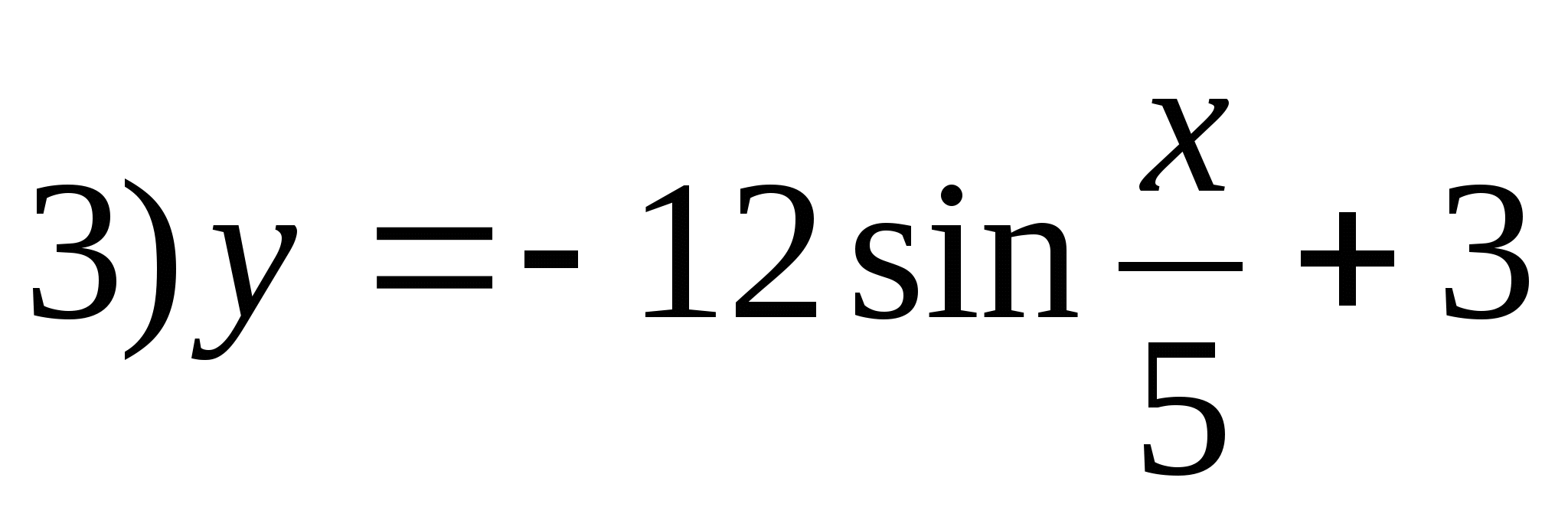
6. Nájdite súčet celých čísel zahrnutých v množine funkčných hodnôt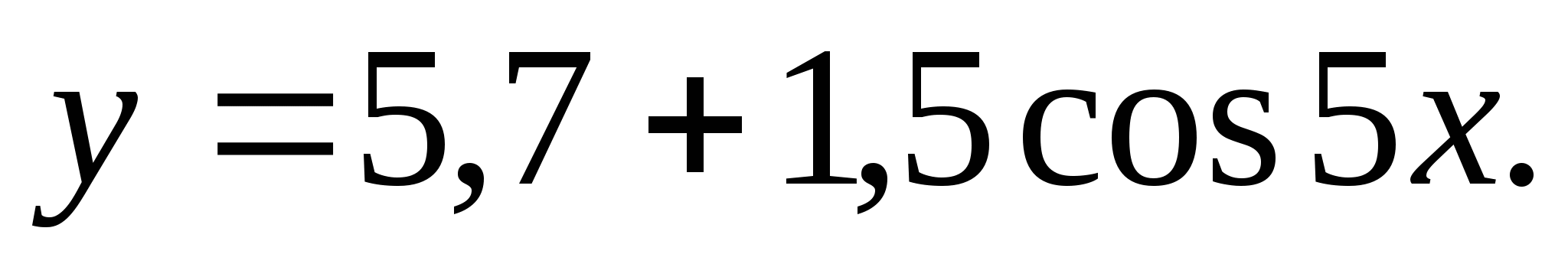

1) 0 2) 7 3) 18 4) 22

7. Nájdite najväčšiu hodnotu funkcie
na segmente

1) 0,5 2) 1,5 3) 0 4) 2

Možnosť 6

1. Zadajte segment zodpovedajúci množine funkčných hodnôt

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Nájdite rozsah funkcie

3. Zadajte najväčšie číslo z rozsahu funkcie

1) 5 2) -6 3) -3 4) 4

4. Ktoré z nasledujúcich čísel je zahrnuté v množine funkčných hodnôt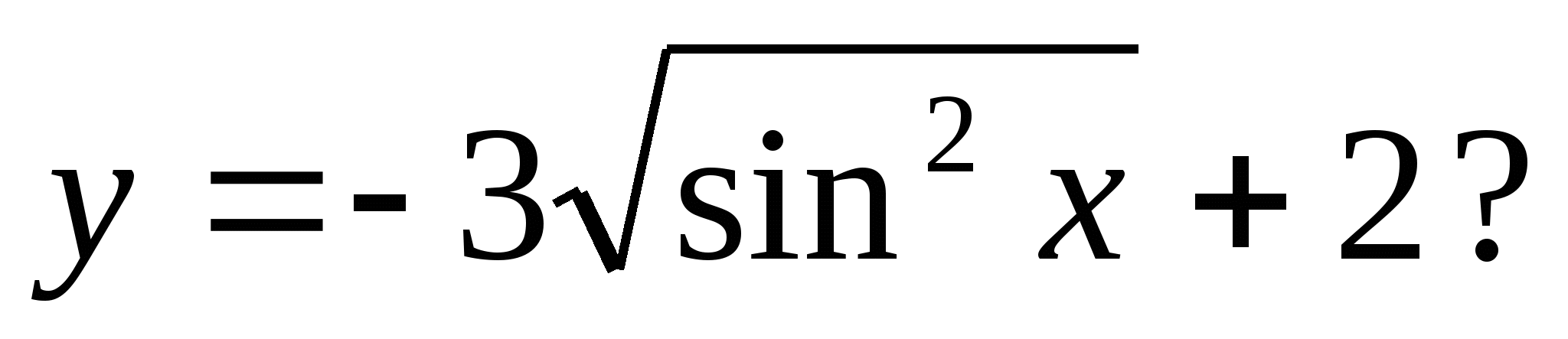

1) 5 2) 0 3) -3 4) 4

5. Zadajte funkciu, ktorej množinou hodnôt je interval .

1) pri = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) r = 5 cos 4 X 4) r = - tg 2 X + 1

6. Nájdite súčin celých čísel zahrnutých v množine hodnôt

r = 3,8 – 1,4 hriech 3 X.

1) 17 2) 12 3) 0 4) 60

7. Nájdite množinu funkčných hodnôt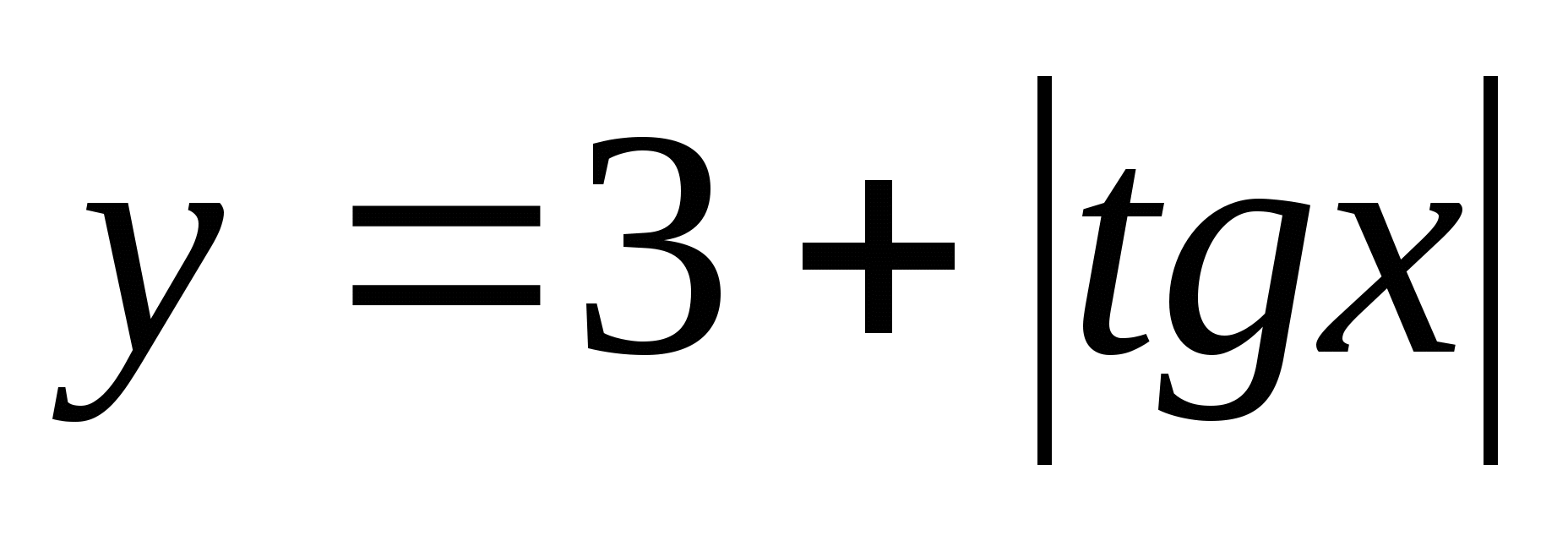
medzi

1) (3;4) 2) 3)

Možnosť 7

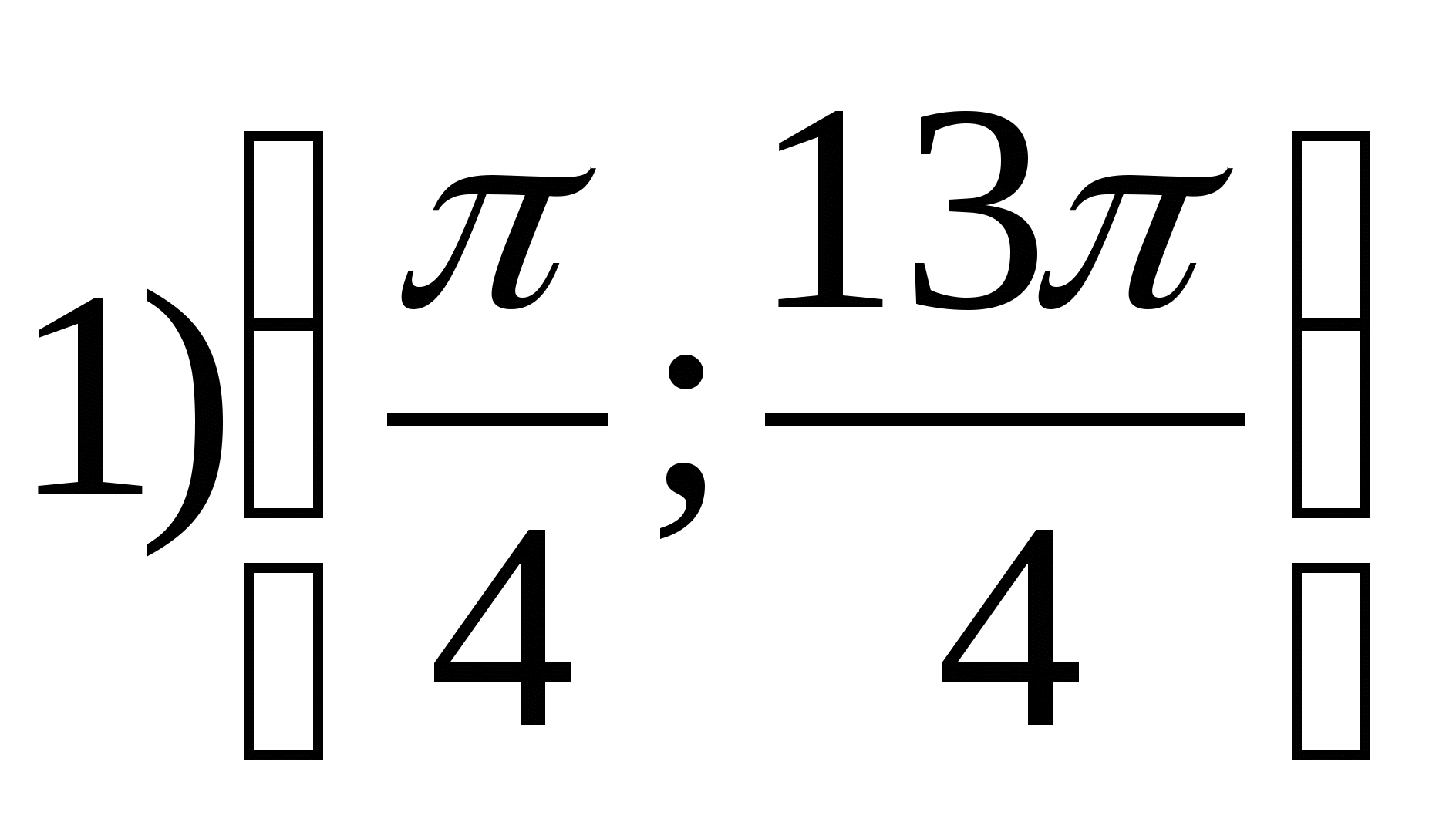
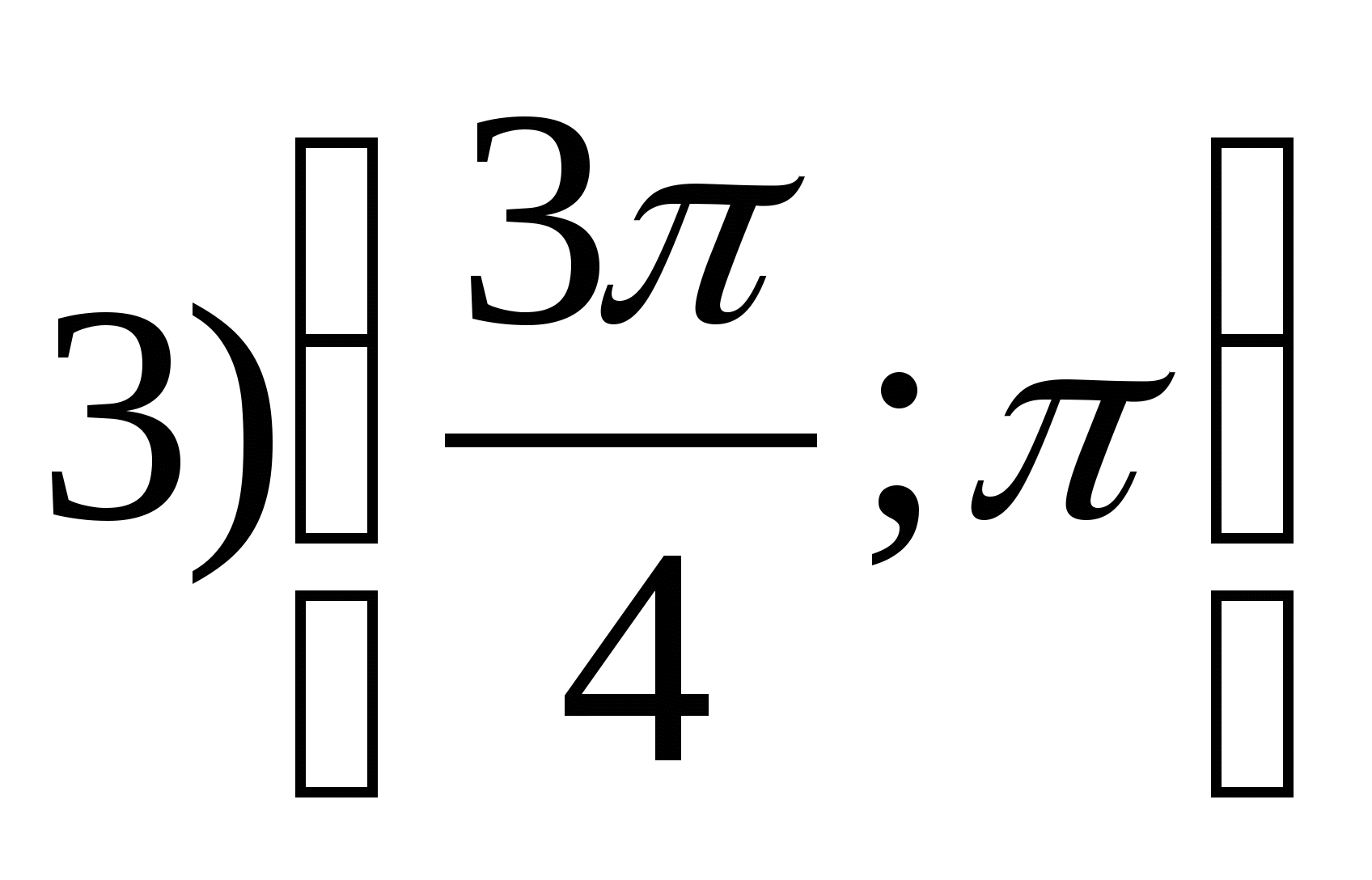
2. Nájdite najmenšiu celočíselnú hodnotu funkcie

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. Pre aké hodnoty a platí rovnicahriech(3 X-4)+5= a riešiteľný?

1) 2) 3) (4;6) 4) (-6;4]

hriech 2 2 X – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

medzi

2) 0 3) 1

r = 4 hriech(X 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Možnosť 8

1. Nájdite množinu funkčných hodnôtr = arctgX- 2π.

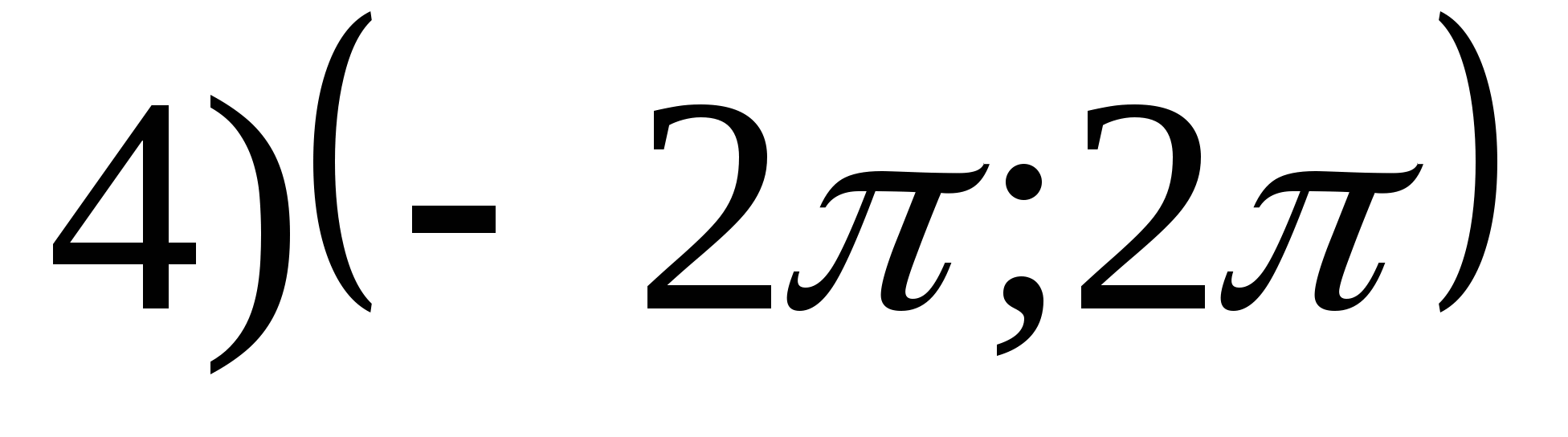
2. Nájdite najväčšiu hodnotu funkcie

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie

1) -4 2) -2 3) 0 4) 2

4. Pre aké hodnoty p rovnice -2+cos(4 X-1)= p má korene?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Nájdite množinu funkčných hodnôtr = -2 tg 2 X + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

medzi
.

1) 0 2) 1 3) -1 4) 3

7. Koľko celých čísel je v rozsahu funkcie

1) 4 2) 3 3) 5 4) 2

Možnosť 9

1. Nájdite rozsah funkcie

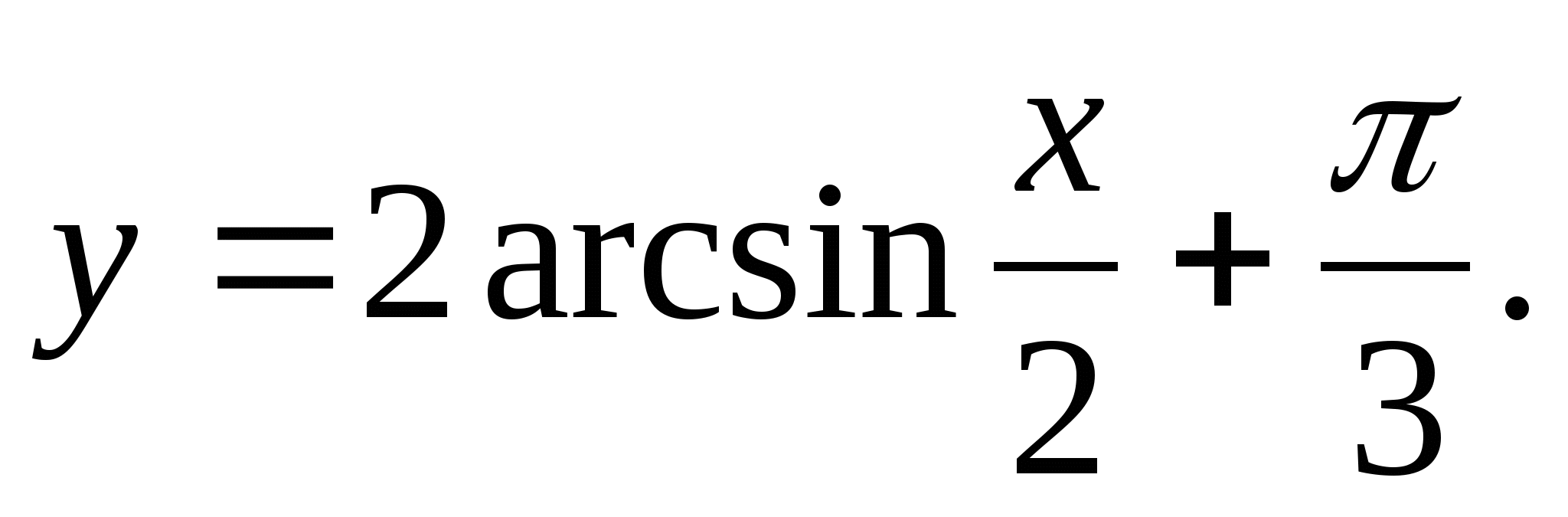
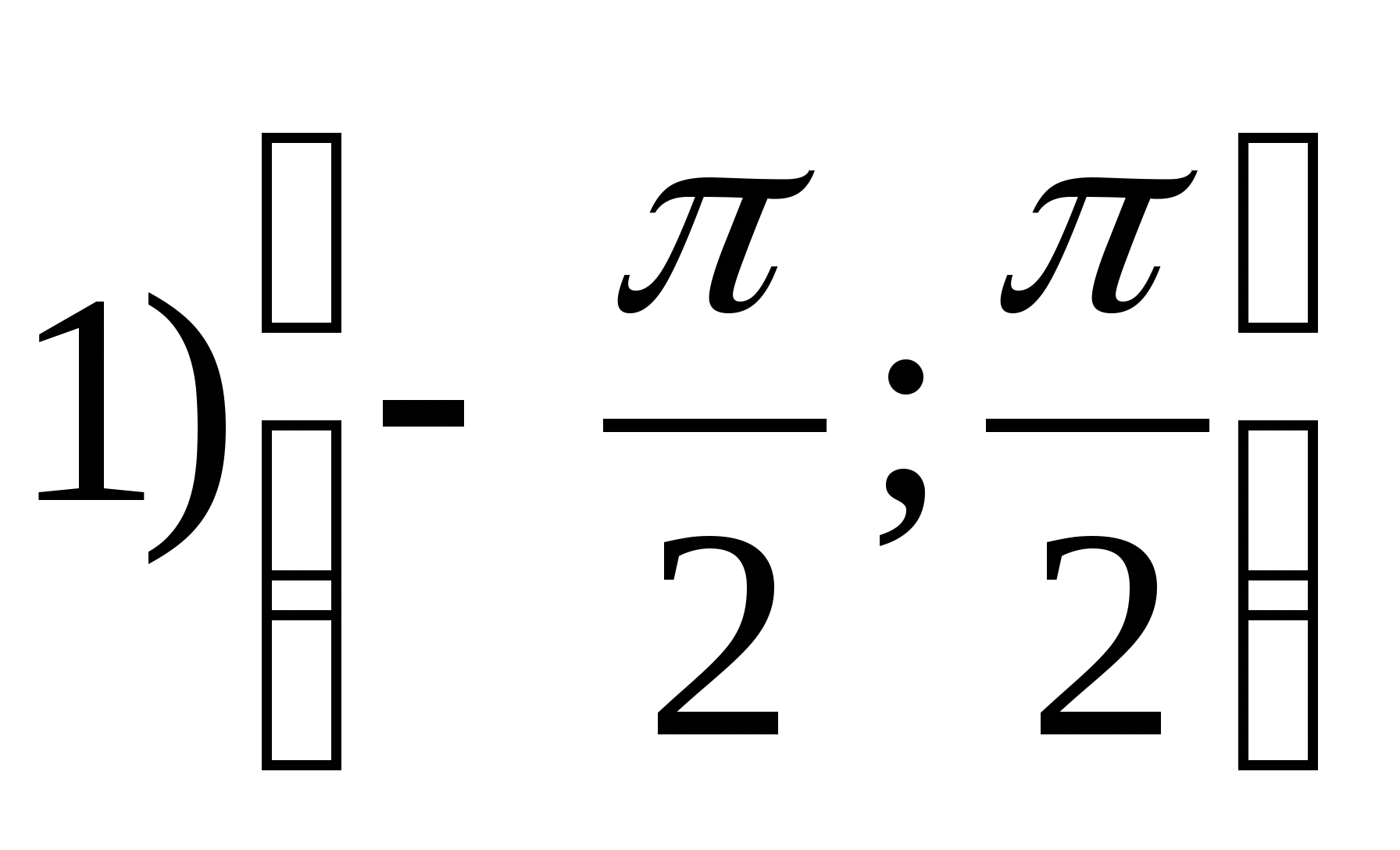
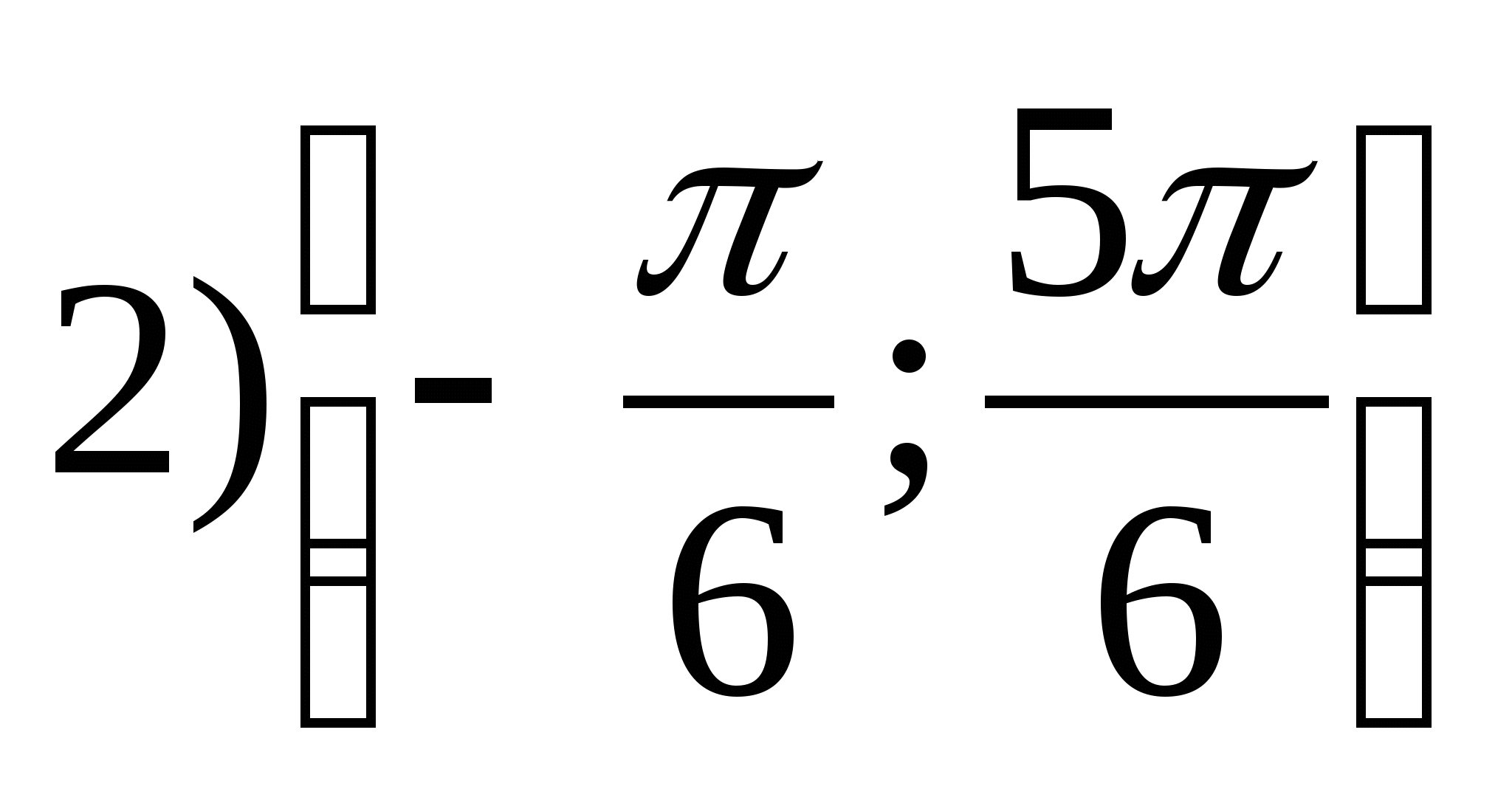
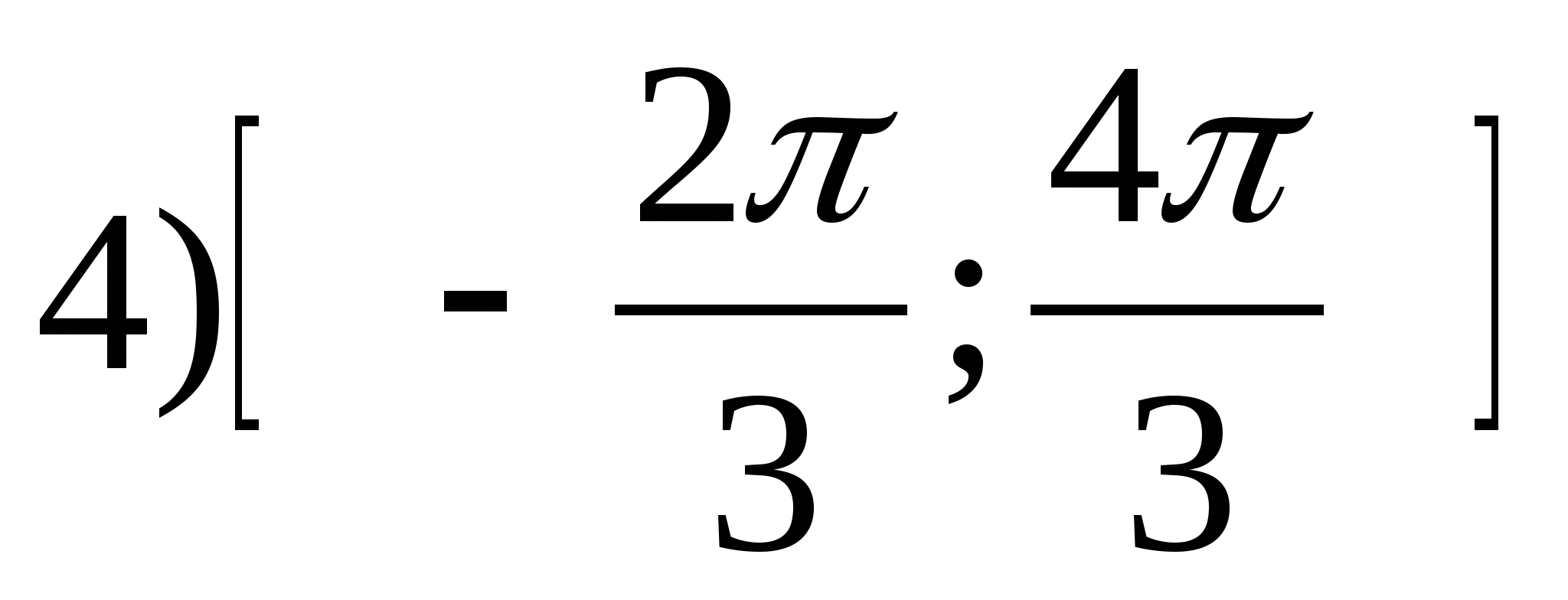
2. Nájdite najväčšiu celočíselnú hodnotu funkcie

1) 4 2) 5 3) 6 4) 7

3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie

1) 0 2) 3 3) 6 4) 9

k rovnica - k + hriech(2 X-1) = 2 riešiteľné?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Nájdite množinu funkčných hodnôt podľa \u003d -cos 2 3 X + 4.

1) 2) 3) 4)

6. Zadajte najmenšiu hodnotu funkcie
medzi

2) -1 3) 0 4) 1

7. Zistite, koľko celých čísel je v rozsahu funkcie y = 12cos 3 X +5 hriech 3 X.

1) 13 2) 27 3) 26 4) 14

Možnosť 10

1. Nájdite rozsah funkcie

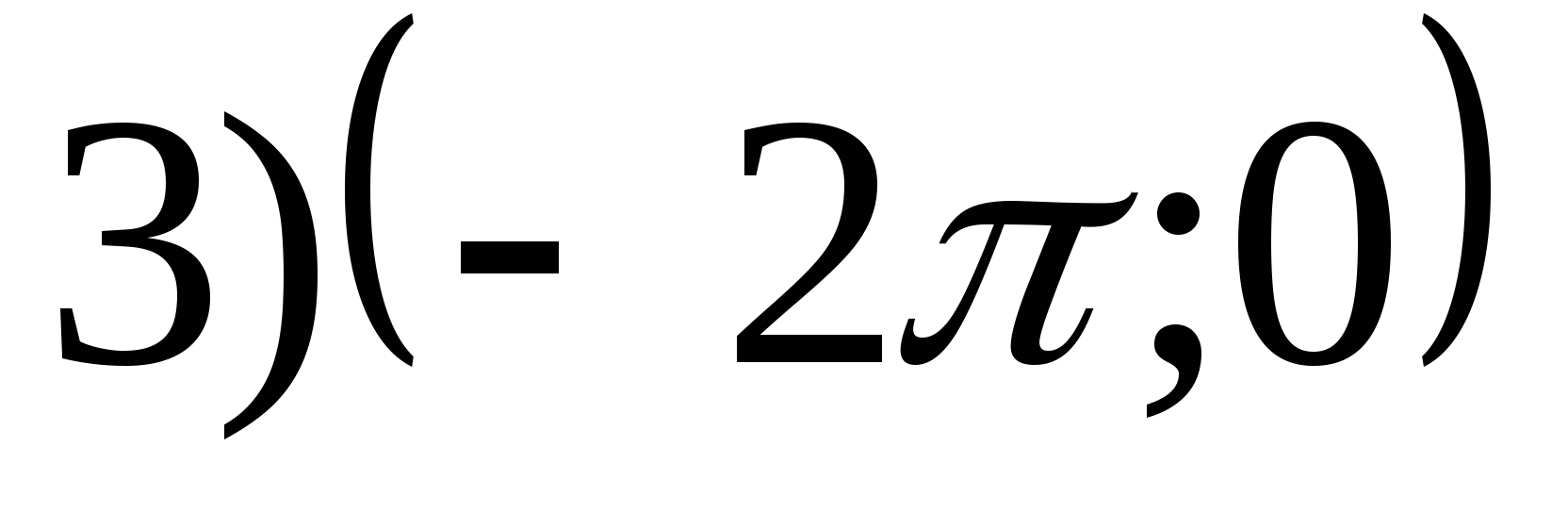
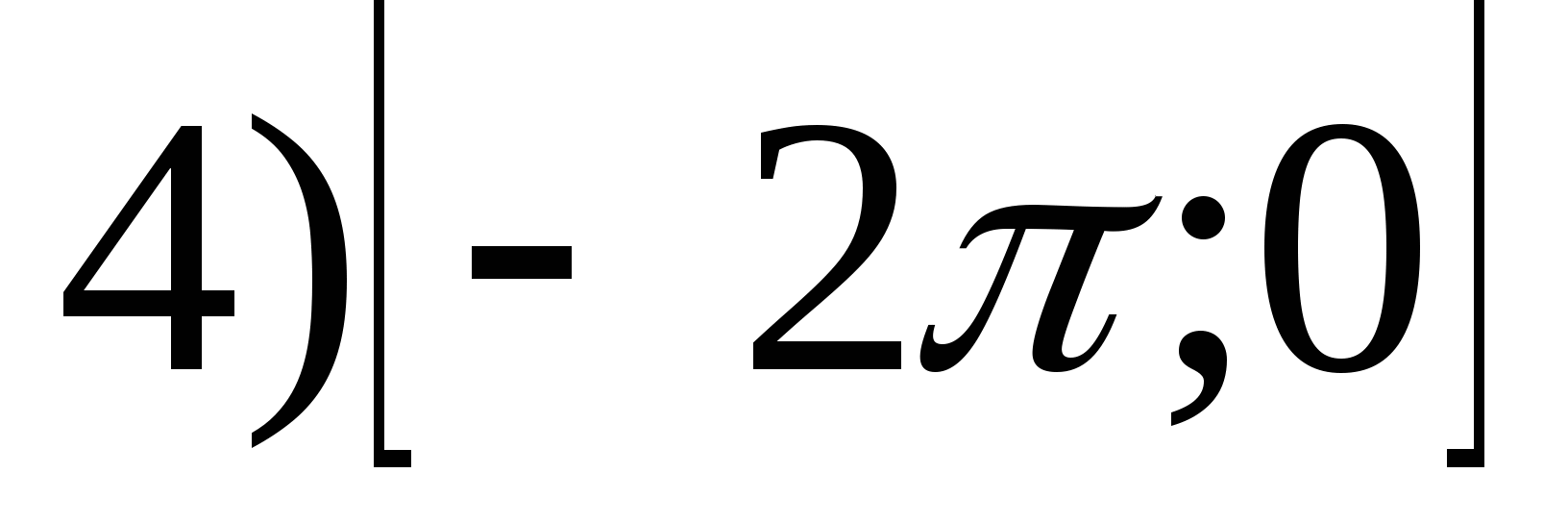
2. Nájdite najmenšiu hodnotu funkcie

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Ktoré z nasledujúcich čísel môže byť hodnotou funkcie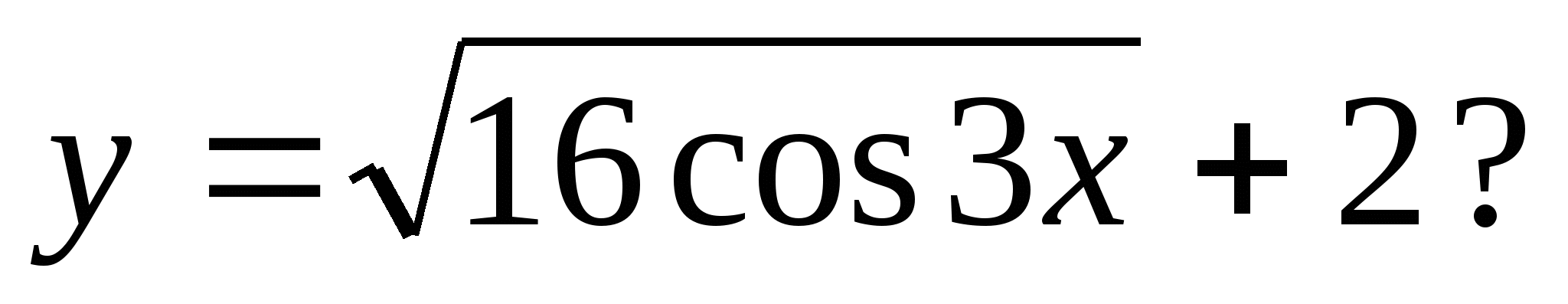

1) -4 2) -1 3) 3 4) 7

4. Pri akých hodnotách parametram rovnica cos (3 X + 2)- m= 5 má korene?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Nájdite množinu funkčných hodnôt podľa \u003d -2ctg 2 3 X + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Zadajte najväčšiu hodnotu funkcie
medzi

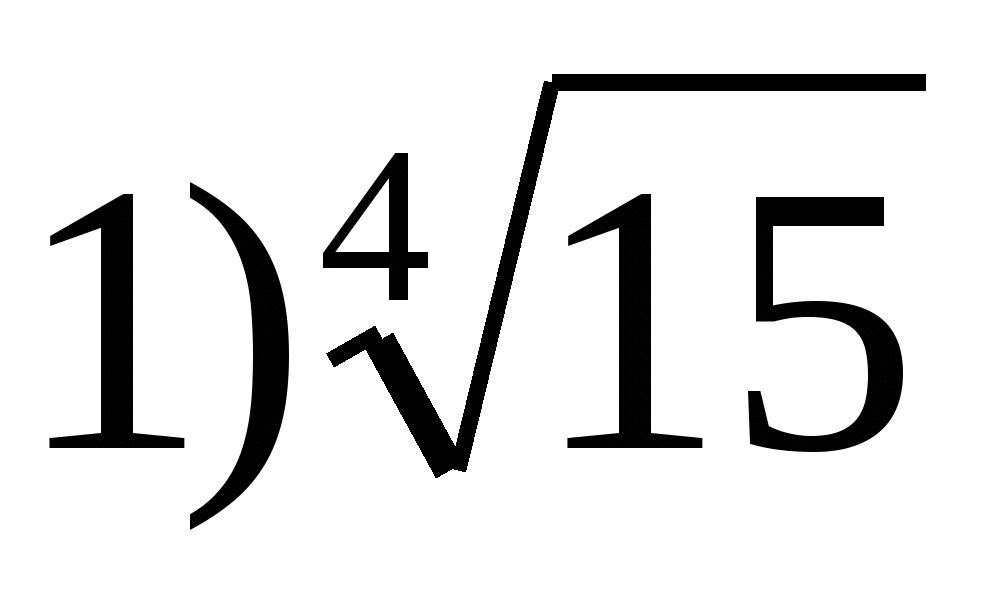2) 0 3) 2 4) 1

7. Zistite, koľko celých čísel je v rozsahu funkcie

1) 30 2) 35 3) 17 4) 7

Sada hodnôt exponenciálnych a logaritmických funkcií

možnosť 1

1. Nájdite rozsah funkcie

1) 4) (-∞;3)

2. Zadajte množinu funkčných hodnôt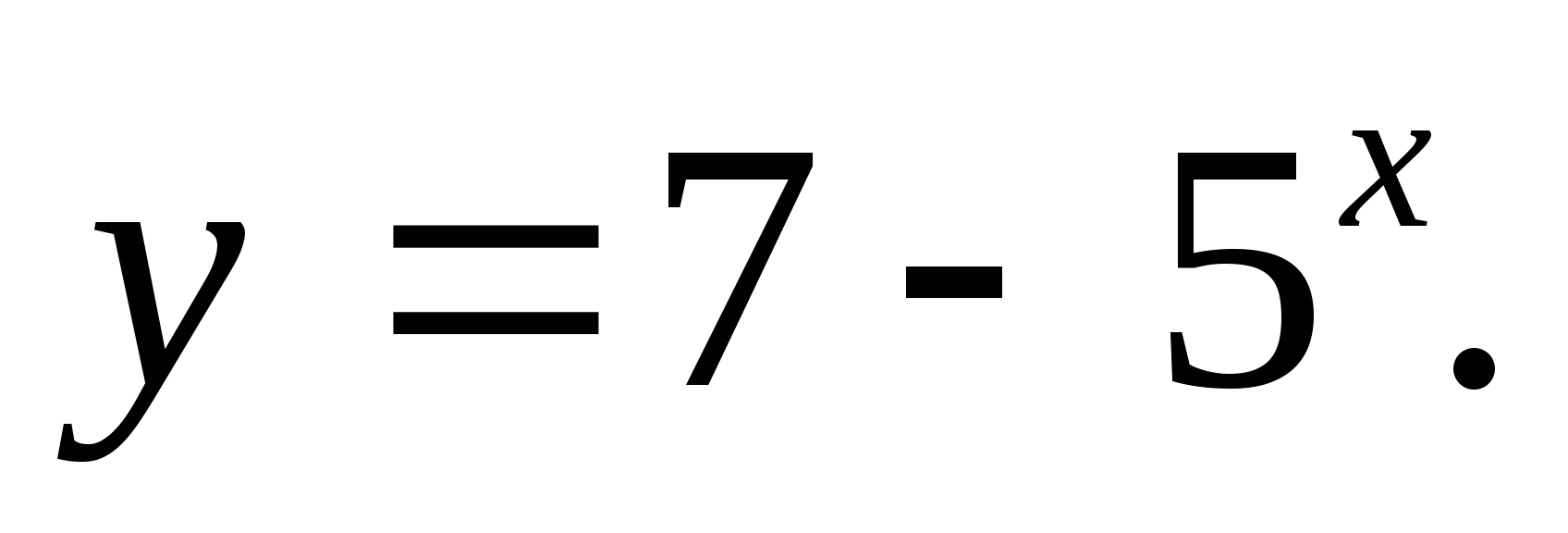

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Zadajte najmenšiu celočíselnú hodnotu funkcie

1) 1 2) -1 3) 0 4) -5

7. Zadajte funkciu, ktorej množinou hodnôt je interval (1;∞).

Možnosť 2

1. Zadajte množinu funkčných hodnôt

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Nájdite rozsah funkcie

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Zadajte najmenšiu celočíselnú hodnotu funkcie

1) -12 2) -11 3) -10 4) -15

4. Zadajte číslo, ktoré nepatrí do množiny funkčných hodnôt

1) -42 2) 3 3) 1 4) -20

5. Zadajte množinu funkčných hodnôt

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Zadajte najväčšiu celočíselnú hodnotu funkcie

1) 10 2) 3 3) 9 4) 2

7. Zadajte funkciu, ktorej množinou hodnôt je interval

(-∞;13).

Možnosť 5

1. Zadajte najmenšiu celočíselnú hodnotu funkcie

1) 0 2) -1 3) -2 4) -3

2. Ktoré z nasledujúcich čísel je v rozsahu funkcie

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Nájdite, na ktorom segmente je funkcia
nadobúda najväčšiu hodnotu 2 a najmenšiu hodnotu -3.

1) 2) (-5;2) 3) 4) (-3;2)

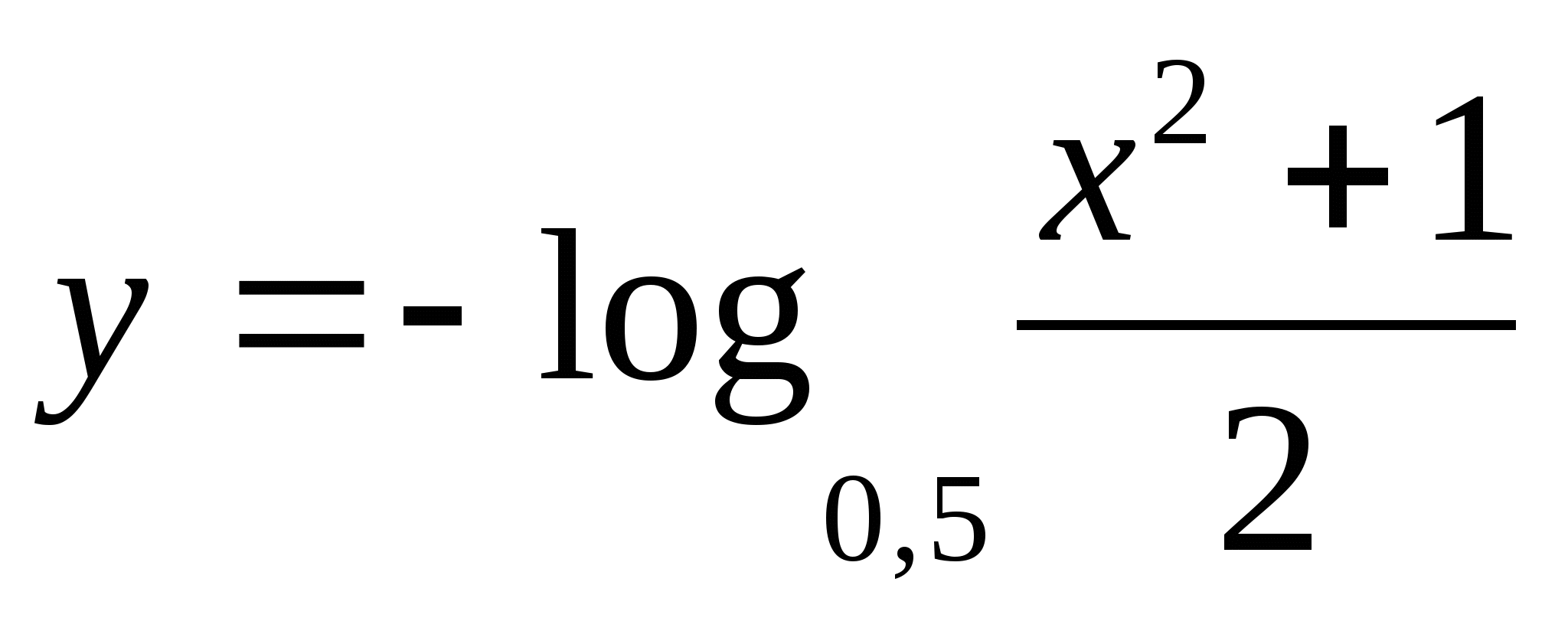medzi

1) -1/2 2) 5 3) 2 4) 4

8. Nájdite súčet všetkých prirodzených čísel, ktoré nie sú zahrnuté v množinách hodnôt funkcie

1) 3 2) 6 3) 10 4) 8

Možnosť 6

1. Zadajte najväčšiu celočíselnú hodnotu funkcie

1) 2 2) 4 3) 3 4) 5

2. Ktoré z nasledujúcich čísel nie je v rozsahu funkcie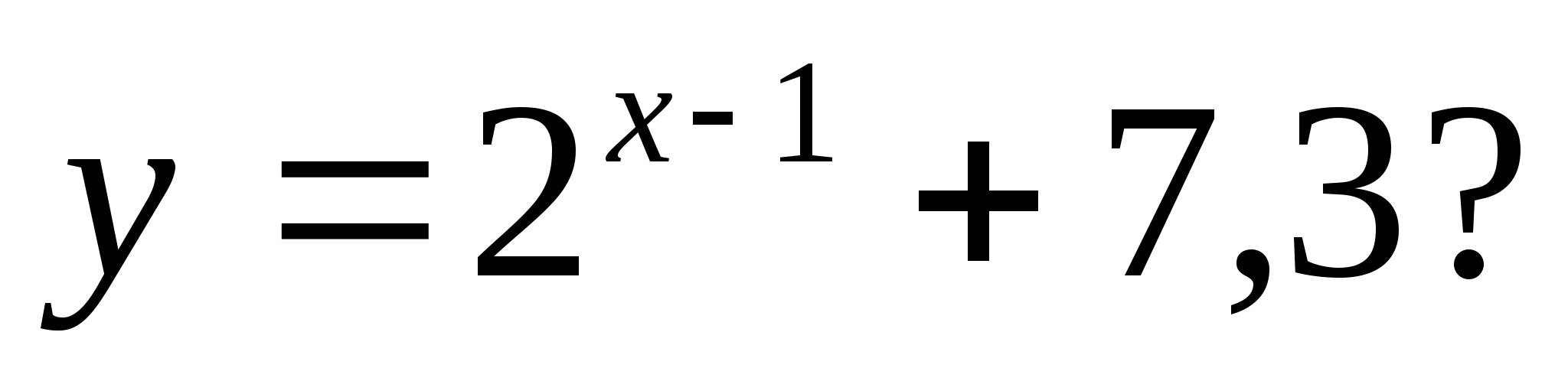

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Zadajte množinu funkčných hodnôt

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Nájdite všetky body na OU, ktoré sú projekciami bodov grafu funkcie

1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)

6. Nájdite, na ktorom segmente je funkcia
má najmenšiu hodnotu ako -2 a najväčšiu hodnotu ako 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Zadajte najväčšiu hodnotu funkcie
medzi

[-0,9; 0]. 2. Nájdite najmenšiu hodnotu funkcie na segmente.

4. Koľko celočíselných hodnôt má funkcia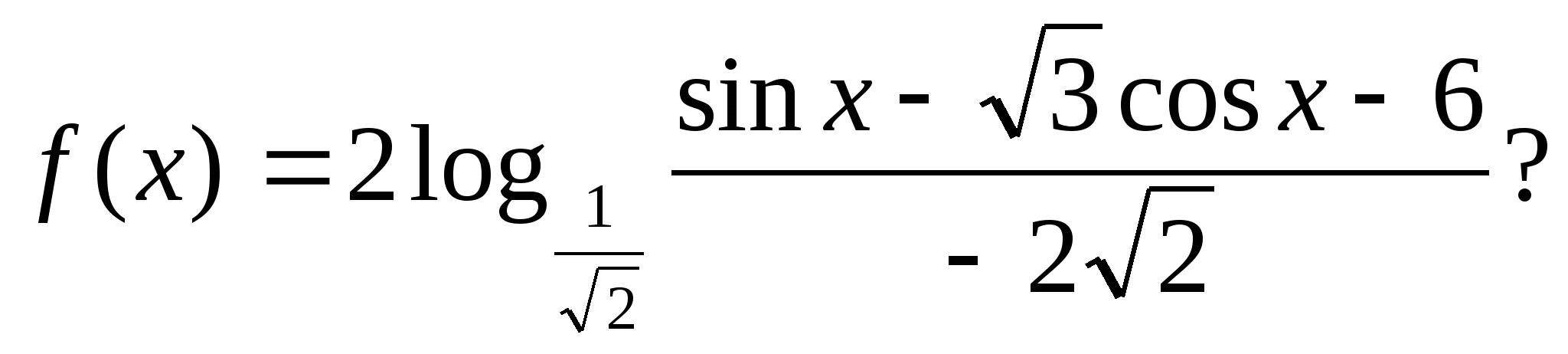

Odpovede

Časť 1

Množina hodnôt exponenciálnych a logaritmických funkcií

Časť 2

Pojem funkcie a všetko, čo s tým súvisí, je tradične zložitý, nie úplne pochopený. Osobitným kameňom úrazu pri štúdiu funkcie a príprave na skúšku je oblasť definície a rozsahu hodnôt (zmeny) funkcie.
Študenti často nevidia rozdiel medzi doménou funkcie a doménou jej hodnôt.
A ak sa študentom podarí zvládnuť úlohy hľadania domény definície funkcie, potom im úlohy hľadania množiny hodnôt funkcie spôsobujú značné ťažkosti.
Účel tohto článku: oboznámenie sa s metódami hľadania hodnôt funkcie.
V dôsledku zohľadnenia tejto témy sa študoval teoretický materiál, zvážili sa metódy riešenia problémov hľadania množín funkčných hodnôt, vybral sa didaktický materiál pre samostatnú prácu študentov.
Tento článok môže učiteľ využiť pri príprave študentov na záverečné a prijímacie skúšky, pri štúdiu témy „Obsah funkcie“ na voliteľných hodinách vo výberových predmetoch z matematiky.

I. Určenie rozsahu funkcie.

Oblasť (množina) hodnôt E(y) funkcie y = f(x) je množina takých čísel y 0 , pre každé z nich existuje také číslo x 0, že: f(x 0) = y 0 .

Pripomeňme si rozsahy hlavných elementárnych funkcií.

Zvážte tabuľku.

Funkcia	Veľa hodnôt
y = kx + b	E(y) = (-∞;+∞)
y=x2n	E(y) =
y = cos x	E(y) = [-1;1]
y = tg x	E(y) = (-∞;+∞)
y = ctg x	E(y) = (-∞;+∞)
y = arcsin x	E(y) = [-π/2; π/2]
y = arcos x	E(y) =
y = arktan x	E(y) = (-π/2 ; π/2)
y = arcctg x	E(y) = (0; π)

Všimnite si tiež, že rozsah akéhokoľvek polynómu párneho stupňa je interval , kde n je najväčšia hodnota tohto polynómu.

II. Vlastnosti funkcie používané pri hľadaní rozsahu funkcie

Na úspešné nájdenie množiny hodnôt funkcie je potrebné dobre poznať vlastnosti základných elementárnych funkcií, najmä ich definičné domény, rozsahy hodnôt a povahu monotónnosti. Uveďme si vlastnosti spojitých, monotónnych diferencovateľných funkcií, ktoré sa najčastejšie používajú pri hľadaní množiny hodnôt funkcií.

Vlastnosti 2 a 3 sa zvyčajne používajú spolu s vlastnosťou elementárnej funkcie byť spojitá vo svojom obore. V tomto prípade sa najjednoduchšie a najkratšie riešenie problému nájdenia množiny hodnôt funkcie dosiahne na základe vlastnosti 1, ak je možné jednoduchými metódami určiť monotónnosť funkcie. Riešenie úlohy sa ďalej zjednoduší, ak je funkcia navyše párna alebo nepárna, periodická atď. Preto pri riešení problémov hľadania množín funkčných hodnôt by sa mali skontrolovať a podľa potreby použiť nasledujúce vlastnosti funkcie:

• kontinuita;
• monotónna;
• diferencovateľnosť;
• párne, nepárne, periodické atď.

Jednoduché úlohy na nájdenie množiny funkčných hodnôt sú väčšinou orientované:

a) použitie najjednoduchších odhadov a obmedzení: (2 x > 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x? 1 atď.);

b) výber celého štvorca: x 2 - 4x + 7 \u003d (x - 2) 2 + 3;

c) na transformáciu goniometrických výrazov: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

d) pomocou monotónnosti funkcie x 1/3 + 2 x-1 sa zvýši o R.

III. Zvážte spôsoby, ako nájsť rozsahy funkcií.

a) postupné zisťovanie hodnôt argumentov zložitých funkcií;
b) metóda hodnotenia;
c) využitie vlastností spojitosti a monotónnosti funkcie;
d) použitie derivátu;
e) použitie najväčších a najmenších hodnôt funkcie;
f) grafická metóda;
g) metóda zavádzania parametrov;
h) metóda inverznej funkcie.

Podstatu týchto metód odhalíme na konkrétnych príkladoch.

Príklad 1: Nájdite rozsah E(y) funkcie y = log 0,5 (4 - 2 3 x - 9 x).

Vyriešme tento príklad postupným hľadaním hodnôt argumentov zložitých funkcií. Po vybratí celého štvorca pod logaritmom transformujeme funkciu

y = log 0,5 (5 - (1 + 2 3 x - 3 2x)) = log 0,5 (5 - (3 x + 1) 2)

A postupne nájdite množiny hodnôt jeho zložitých argumentov:

E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)

Označiť t= 5 – (3 x +1) 2, kde -∞≤ t≤4. Problém sa teda redukuje na nájdenie množiny hodnôt funkcie y = log 0,5 t na lúči (-∞;4) . Keďže funkcia y = log 0,5 t je definovaná iba pri, potom sa jej množina hodnôt na lúči (-∞;4) zhoduje s množinou hodnôt funkcie na intervale (0;4), ktorý je priesečník lúča (-∞;4) s doménou definície (0;+∞) logaritmickej funkcie. Na intervale (0;4) je táto funkcia spojitá a klesajúca. O t> 0, má tendenciu k +∞ a kedy t = 4 nadobúda hodnotu -2, takže E(y) =(-2, +∞).

Príklad 2: Nájdite rozsah funkcie

y = cos7x + 5cosx

Riešime tento príklad metódou odhadov, ktorej podstatou je odhadnúť spojitú funkciu zdola a zhora a dokázať, že funkcia dosahuje dolnú a hornú hranicu odhadov. V tomto prípade je zhoda množiny hodnôt funkcie s intervalom od dolnej hranice odhadu po hornú určená kontinuitou funkcie a absenciou iných hodnôt.

Z nerovností -1≤cos7x?1, -5≤5cosx?5 dostaneme odhad -6≤y?6. Pre x = p a x = 0 má funkcia hodnoty -6 a 6, t.j. dosahuje dolnú a hornú hranicu. Ako lineárna kombinácia spojitých funkcií cos7x a cosx je funkcia y spojitá pozdĺž celej číselnej osi, preto vlastnosťou spojitej funkcie nadobúda všetky hodnoty od -6 do 6 vrátane a iba ich, keďže , v dôsledku nerovností -6≤y?6, iné hodnoty nie sú možné. v dôsledku toho E(y)= [-6;6].

Príklad 3: Nájdite rozsah E(f) funkcie f(x)= cos2x + 2cosx.

Pomocou vzorca dvojitého uhla kosínus transformujeme funkciu f(x)= 2cos 2 x + 2cosx – 1 a označte t= cosx. Potom f(x)= 2t 2 + 2t – 1. Keďže E(cosx) =

[-1;1], potom rozsah funkcie f(x) sa zhoduje s množinou hodnôt funkcie g (t)\u003d 2t 2 + 2t - 1 na segmente [-1; 1], ktorý nájdeme grafickou metódou. Po vynesení funkcie y = 2t 2 + 2t - 1 = 2(t + 0,5) 2 - 1,5 na interval [-1; 1] zistíme E(f) = [-1,5; 3].

Poznámka – Veľa problémov s parametrom sa redukuje na nájdenie množiny hodnôt funkcie, ktoré súvisia najmä s riešiteľnosťou a počtom riešení rovnice a nerovníc. Napríklad rovnica f(x)= a je riešiteľné vtedy a len vtedy

aE(f) Podobne aj rovnica f(x)= a má aspoň jeden koreň umiestnený na nejakom intervale X alebo nemá na tomto intervale žiadny koreň vtedy a len vtedy, ak a patrí alebo nepatrí do množiny hodnôt funkcie f(x) na intervale X. Študujeme aj pomocou množiny hodnôt funkcie a nerovníc f(x)≠ a, f(x)> atď. najmä f(x)≠ a pre všetky prípustné hodnoty x, ak a E(f)

Príklad 4. Pre aké hodnoty parametra a má rovnica (x + 5) 1/2 = a (x 2 + 4) jeden koreň na segmente [-4;-1].

Napíšme rovnicu v tvare (x + 5) 1/2 / (x 2 + 4) = a. Posledná rovnica má aspoň jeden koreň na segmente [-4;-1] vtedy a len vtedy, ak a patrí do množiny hodnôt funkcie f(x) =(x + 5) 1/2 / (x 2 + 4) na segmente [-4;-1]. Nájdite túto množinu pomocou vlastnosti spojitosti a monotónnosti funkcie.

Na segmente [-4;-1] je funkcia y = xІ + 4 spojitá, klesajúca a kladná, preto funkcia g(x) = 1/(x 2 + 4) je spojité a na tomto segmente sa zväčšuje, keďže pri delení kladnou funkciou sa charakter monotónnosti funkcie mení na opačný. Funkcia h(x) =(x + 5) 1/2 je spojitá a rastúca vo svojom obore D(h) =[-5;+∞) a najmä na intervale [-4;-1], kde je tiež kladný. Potom funkcia f(x)=g(x) h(x), ako súčin dvoch spojitých, rastúcich a kladných funkcií, je tiež spojitý a zvyšuje sa na segmente [-4;-1], preto jeho množinou hodnôt na [-4;-1] je segment [ f(-4); f(-1)] = . Preto rovnica má riešenie na intervale [-4;-1] a jediné (vlastnosťou spojitej monotónnej funkcie) pre 0,05 ≤ a ≤ 0,4

Komentujte. Riešiteľnosť rovnice f(x) = a na nejakom intervale X je ekvivalentné príslušnosti hodnôt parametra a súbor funkčných hodnôt f(x) na X. Preto množina hodnôt funkcie f(x) na intervale X sa zhoduje so súborom hodnôt parametrov a, pre ktoré platí rovnica f(x) = a má aspoň jeden koreň na intervale X. Najmä rozsah hodnôt E(f) funkcie f(x) zodpovedá množine hodnôt parametrov a, pre ktoré platí rovnica f(x) = a má aspoň jeden koreň.

Príklad 5: Nájdite rozsah E(f) funkcie

Vyriešme príklad zavedením parametra, podľa ktorého E(f) zodpovedá množine hodnôt parametrov a, pre ktoré platí rovnica

má aspoň jeden koreň.

Keď a=2, rovnica je lineárna - 4x - 5 = 0 s nenulovým koeficientom pri neznámej x, preto má riešenie. Pre a≠2 je rovnica kvadratická, takže je riešiteľná vtedy a len vtedy, ak je jej diskriminant

Keďže bod a = 2 patrí do segmentu

potom požadovaný súbor hodnôt parametrov a, teda rozsah hodnôt E(f) bude celý segment.

Za priamy vývoj metódy zavedenia parametra pri hľadaní množiny hodnôt funkcie môžeme považovať metódu inverznej funkcie, na nájdenie ktorej je potrebné vyriešiť rovnicu pre x f(x)=y, pričom y považujeme za parameter. Ak má táto rovnica jedinečné riešenie x=g(y), potom rozsah E(f) pôvodná funkcia f(x) sa zhoduje s doménou definície D(g) inverzná funkcia g(y). Ak rovnica f(x)=y má viacero riešení x = g 1 (y), x \u003d g 2 (y) atď., teda E(f) sa rovná spojeniu rozsahov definícií funkcií g 1 (y), g 2 (y) atď.

Príklad 6: Nájdite rozsah E(y) funkcie y = 5 2/(1-3x).

Z rovnice

nájdite inverznú funkciu x = log 3 ((log 5 y – 2)/(log 5 y)) a jej definičný obor D(x):

Pretože rovnica pre x má jedinečné riešenie

E(y) = D(x) = (0; 1) (25;+°).

Ak doména funkcie pozostáva z niekoľkých intervalov alebo funkcia v rôznych intervaloch je daná rôznymi vzorcami, potom, aby ste našli doménu funkcie, musíte nájsť množiny hodnôt funkcie v každom intervale a vziať ich únie.

Príklad 7: Nájdite rozsahy f(x) a f(f(x)), kde

f(x) na lúči (-∞;1], kde sa zhoduje s výrazom 4 x + 9 4 -x + 3. Označ. t = 4 x. Potom f(x) = t + 9/t + 3, kde 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) na lúči (-∞;1] sa zhoduje s množinou hodnôt funkcie g(t) = t + 9/t + 3, na intervale (0;4], ktorý nájdeme pomocou derivácie g'(t) \u003d 1 - 9 / t 2. Na intervale (0;4] derivácia g'(t) je definovaný a zaniká tam pri t = 3. O 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g(t) klesá a v intervale (3;4) sa zvyšuje, pričom zostáva súvislý na celom intervale (0;4), takže g (3)= 9 - najmenšia hodnota tejto funkcie na intervale (0; 4], pričom jej najväčšia hodnota neexistuje, takže keď t→0 správnu funkciu g(t)→+∞. Potom vlastnosťou spojitej funkcie množina hodnôt funkcie g(t) na intervale (0;4], a teda množine hodnôt f(x) na (-∞;-1], bude lúč .

Teraz kombináciou intervalov - množín funkčných hodnôt f(f(x)), označovať t = f(x). Potom f(f(x)) = f(t), kde t funkciu f(t)= 2 cos( x-1) 1/2+ 7 a opäť nadobúda všetky hodnoty od 5 do 9 vrátane, t.j. rozsah E(fІ) = E(f(f(x))) =.

Podobne označovanie z = f(f(x)), rozsah nájdete E(f3) funkcie f(f(f(x))) = f(z), kde 5 ≤ z ≤ 9 atď. Uistite sa, že E(f3) = .

Najuniverzálnejšia metóda na nájdenie množiny funkčných hodnôt je použitie najväčšej a najmenšej hodnoty funkcie v danom intervale.

Príklad 8. Pre aké hodnoty parametra R nerovnosť 8 x - p ≠ 2x+1 – 2x platí pre všetky -1 ≤ x< 2.

Označenie t = 2 x, zapíšeme nerovnosť ako p ≠ t 3 - 2 t 2 + t. Pretože t = 2 x je neustále sa zvyšujúca funkcia zapnutá R, potom pre -1 ≤ x< 2 переменная

2 -1 ≤ t<2 2 ↔

0,5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда R odlišné od funkčných hodnôt f(t) \u003d t3 - 2t2 + t pri 0,5 ≤ t< 4.

Najprv nájdime množinu hodnôt funkcie f(t) na intervale, kde má všade deriváciu f'(t) = 3t2 - 4t + 1. v dôsledku toho f(t) je diferencovateľná, a teda kontinuálna na segmente . Z rovnice f'(t) = 0 nájsť kritické body funkcie t=1/3, t=1, z ktorých prvý nepatrí do segmentu a druhý do neho patrí. Pretože f(0,5) = 1/8, f(1) = 0, f(4) = 36, potom podľa vlastnosti diferencovateľnej funkcie je 0 najmenšia a 36 je najväčšia hodnota funkcie f(t) na segmente. Potom f(t), ako spojitá funkcia preberá v segmente všetky hodnoty od 0 do 36 vrátane a hodnota 36 nadobúda iba vtedy, keď t = 4, takže pre 0,5 ≤ t< 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Zoberme si problém, v ktorom je potrebné určiť rozsah hodnôt arcsínusu.

Príklad 1

podmienka: nájdite rozsah y = a r c sin x .

Riešenie

Vo všeobecnom prípade sa definičný obor arcsínusu nachádza na intervale [ - 1 ; jeden]. Musíme na ňom určiť najväčšiu a najmenšiu hodnotu zadanej funkcie.

y "= a rc sin x" = 1 1 - x 2

Vieme, že derivácia funkcie bude kladná pre všetky hodnoty x nachádzajúce sa v intervale [ - 1 ; 1 ] , to znamená, že v celej oblasti definície sa funkcia arksínus zvýši. To znamená, že najmenšiu hodnotu nadobudne, keď sa x rovná – 1, a najväčšiu – keď sa x rovná 1.

mi n x ∈ - 1; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2

Rozsah arcsínusovej funkcie sa teda bude rovnať E (a rc sin x) = - π 2 ; π 2.

odpoveď: E (a rc sin x) \u003d - π 2; π 2

Príklad 2

podmienka: vypočítajte rozsah y = x 4 - 5 x 3 + 6 x 2 na danom intervale [ 1 ; štyri].

Riešenie

Stačí nám vypočítať najväčšiu a najmenšiu hodnotu funkcie v danom intervale.

Na určenie extrémnych bodov je potrebné vykonať nasledujúce výpočty:

y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 a 1 a 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1 ;4 ;x3 = 15 + 338 ≈ 2,59 ∈ 1;4

Teraz nájdime hodnoty danej funkcie na koncoch segmentu a bodoch x 2 = 15 - 33 8 ; x 3 \u003d 15 + 33 8:

r (1) = 1 4 - 5 1 3 + 6 1 2 = 2 r 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 2. 08 r 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 r (4) = 4 4 - 5 4 3 + 6 4 2 = 32

To znamená, že množina funkčných hodnôt bude určená segmentom 117 - 165 33 512 ; 32.

odpoveď: 117 - 165 33 512 ; 32 .

Prejdime k hľadaniu množiny hodnôt spojitej funkcie y = f (x) v intervaloch (a; b) a a; + ∞ , - ∞ ; b, -°; +∞ .

Začnime určením najväčšieho a najmenšieho bodu, ako aj intervalov nárastu a poklesu v danom intervale. Potom budeme musieť vypočítať jednostranné limity na koncoch intervalu a / alebo limity v nekonečne. Inými slovami, musíme určiť správanie funkcie za daných podmienok. Na to máme všetky potrebné údaje.

Príklad 3

podmienka: vypočítajte rozsah funkcie y = 1 x 2 - 4 na intervale (- 2 ; 2) .

Riešenie

Určte najväčšiu a najmenšiu hodnotu funkcie na danom intervale

y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2; 2)

Dostali sme maximálnu hodnotu rovnú 0, keďže práve v tomto bode sa mení znamienko funkcie a graf začína klesať. Pozri ilustráciu:

To znamená, že y (0) = 1 0 2 - 4 = - 1 4 bude maximálna hodnota funkcie.

Teraz definujme správanie funkcie pre x, ktoré má tendenciu - 2 na pravej strane a + 2 na ľavej strane. Inými slovami, nachádzame jednostranné limity:

lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞

Dostali sme, že hodnoty funkcie sa zvýšia z mínus nekonečna na -1 4, keď sa argument zmení z -2 na 0. A keď sa argument zmení z 0 na 2, hodnoty funkcie sa znížia smerom k mínus nekonečnu. Preto množina hodnôt danej funkcie na intervale, ktorý potrebujeme, bude (- ∞ ; - 1 4 ] .

odpoveď: (- ∞ ; - 1 4 ] .

Príklad 4

Podmienka: uveďte množinu hodnôt y = t g x na danom intervale - π 2 ; π 2.

Riešenie

Vieme, že vo všeobecnosti derivácia dotyčnice v - π 2; π 2 bude kladné, to znamená, že funkcia sa zvýši. Teraz definujme, ako sa funkcia správa v rámci daných hraníc:

lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

Získali sme nárast hodnôt funkcie z mínus nekonečna na plus nekonečno, keď sa argument zmení z - π 2 na π 2, a môžeme povedať, že množina riešení tejto funkcie bude množinou všetkých skutočných čísla.

odpoveď: - ∞ ; + ∞ .

Príklad 5

podmienka: určite, aký je rozsah funkcie prirodzeného logaritmu y = ln x .

Riešenie

Vieme, že táto funkcia je definovaná pre kladné hodnoty argumentu D (y) = 0 ; +∞ . Derivácia na danom intervale bude kladná: y " = ln x " = 1 x . To znamená, že funkcia sa na ňom zvyšuje. Ďalej musíme definovať jednostranný limit pre prípad, keď argument ide na 0 (na pravej strane) a keď x ide do nekonečna:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Zistili sme, že hodnoty funkcie sa budú zvyšovať z mínus nekonečna na plus nekonečno, keď sa hodnoty x menia z nuly na plus nekonečno. To znamená, že množina všetkých reálnych čísel je rozsahom funkcie prirodzeného logaritmu.

odpoveď: množina všetkých reálnych čísel je rozsahom funkcie prirodzeného logaritmu.

Príklad 6

podmienka: určte, aký je rozsah funkcie y = 9 x 2 + 1 .

Riešenie

Táto funkcia je definovaná za predpokladu, že x je reálne číslo. Vypočítajme najväčšie a najmenšie hodnoty funkcie, ako aj intervaly jej nárastu a poklesu:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

V dôsledku toho sme určili, že táto funkcia sa zníži, ak x ≥ 0; zvýšiť, ak x ≤ 0 ; má maximálny bod y (0) = 9 0 2 + 1 = 9, keď je premenná 0 .

Pozrime sa, ako sa funkcia správa v nekonečne:

lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0

Zo záznamu je zrejmé, že hodnoty funkcie sa v tomto prípade budú asymptoticky blížiť k 0.

Zhrnutie: keď sa argument zmení z mínus nekonečna na nulu, hodnoty funkcie sa zvýšia z 0 na 9. Keď sa hodnoty argumentov pohybujú od 0 do plus nekonečna, hodnoty zodpovedajúcich funkcií sa znížia z 9 na 0. Znázornili sme to na obrázku:

Ukazuje, že rozsah funkcie bude interval E (y) = (0 ; 9 ]

odpoveď: E (y) = (0 ; 9 ]

Ak potrebujeme určiť množinu hodnôt funkcie y = f (x) na intervaloch [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , potom budeme musieť vykonať presne tie isté štúdie. Tieto prípady zatiaľ nebudeme rozoberať, stretneme sa s nimi neskôr v problémoch .

Čo ak je však doménou určitej funkcie spojenie niekoľkých intervalov? Potom musíme vypočítať množiny hodnôt pre každý z týchto intervalov a skombinovať ich.

Príklad 7

podmienka: určiť, aký bude rozsah y = x x - 2 .

Riešenie

Keďže menovateľ funkcie by sa nemal zmeniť na 0 , potom D (y) = - ∞ ; 2*2; +∞ .

Začnime definovaním množiny funkčných hodnôt na prvom segmente - ∞ ; 2, čo je otvorený nosník. Vieme, že funkcia na nej bude klesať, to znamená, že derivácia tejto funkcie bude záporná.

lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Potom v prípadoch, keď sa argument zmení smerom k mínus nekonečnu, sa hodnoty funkcie asymptoticky priblížia k 1. Ak sa hodnoty x zmenia z mínus nekonečna na 2, potom sa hodnoty znížia z 1 na mínus nekonečno, t.j. funkcia na tomto segmente bude nadobúdať hodnoty z intervalu - ∞ ; jeden . Z nášho uvažovania vylučujeme jednotu, pretože hodnoty funkcie ju nedosahujú, ale iba asymptoticky sa k nej približujú.

Pre otvorený nosník 2 ; + ∞ vykonávame presne tie isté akcie. Funkcia na ňom tiež klesá:

lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

Hodnoty funkcie na tomto segmente sú určené množinou 1; +∞ . To znamená, že rozsah hodnôt funkcie špecifikovanej v podmienke, ktorú potrebujeme, bude zjednotením množín - ∞; 1 a 1; +∞ .

odpoveď: E (y) = - ∞; 1*1; +∞ .

Toto je možné vidieť na grafe:

Špeciálnym prípadom sú periodické funkcie. Ich oblasť hodnoty sa zhoduje so súborom hodnôt v intervale, ktorý zodpovedá obdobiu tejto funkcie.

Príklad 8

podmienka: určte rozsah sínusu y = sin x .

Riešenie

Sínus sa vzťahuje na periodickú funkciu a jej perióda je 2 pi. Vezmeme segment 0; 2 π a uvidíte, aká bude množina hodnôt na ňom.

y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

V rámci 0 ; 2 π funkcia bude mať krajné body π 2 a x = 3 π 2 . Vypočítajme, čomu sa v nich budú rovnať hodnoty funkcie, ako aj na hraniciach segmentu, po ktorých vyberieme najväčšiu a najmenšiu hodnotu.

y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1 , max x ∈ 0 ; 2 π sinx \u003d sin π 2 \u003d 1

odpoveď: E (sinx) = -1; jeden .

Ak potrebujete poznať rozsahy funkcií, ako sú exponenciálne, exponenciálne, logaritmické, trigonometrické, inverzné trigonometrické, odporúčame vám znova si prečítať článok o základných elementárnych funkciách. Teória, ktorú tu uvádzame, nám umožňuje testovať hodnoty tam uvedené. Je žiaduce naučiť sa ich, pretože sú často potrebné pri riešení problémov. Ak poznáte rozsahy hlavných funkcií, potom môžete ľahko nájsť rozsahy funkcií, ktoré sa získajú z elementárnych funkcií pomocou geometrickej transformácie.

Príklad 9

podmienka: určte rozsah y = 3 a r c cos x 3 + 5 π 7 - 4 .

Riešenie

Vieme, že segment od 0 do pi je rozsah inverzného kosínusu. Inými slovami, E (a rc cos x) = 0; π alebo 0 ≤ a rc cos x ≤ π . Funkciu a r c cos x 3 + 5 π 7 dostaneme z arkuskosínusu jeho posunutím a natiahnutím pozdĺž osi O x, no takéto transformácie nám nič nedajú. Preto 0 ≤ a rc cos x 3 + 5 π 7 ≤ π.

Funkciu 3 a r c cos x 3 + 5 π 7 možno získať z inverzného kosínusu a r c cos x 3 + 5 π 7 natiahnutím pozdĺž osi y, t.j. 0 ≤ 3 a rc cos x 3 + 5 π 7 ≤ 3 π. Konečnou transformáciou je posun pozdĺž osi O y o 4 hodnoty. Výsledkom je dvojitá nerovnosť:

0 - 4 ≤ 3 arc cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4

Dostali sme, že rozsah, ktorý potrebujeme, sa bude rovnať E (y) = - 4 ; 3 pi-4.

odpoveď: E(y) = -4; 3 pi-4.

Napíšme ešte jeden príklad bez vysvetlení, pretože je úplne podobný predchádzajúcemu.

Príklad 10

podmienka: vypočítajte, aký bude rozsah funkcie y = 2 2 x - 1 + 3 .

Riešenie

Prepíšme funkciu uvedenú v podmienke ako y = 2 · (2 ​​​​x - 1) - 1 2 + 3 . Pre mocninovú funkciu y = x - 1 2 bude rozsah definovaný na intervale 0 ; + ∞ , t.j. x-12 > 0. V tomto prípade:

2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3

Takže E (y) = 3; +∞ .

odpoveď: E(y) = 3; +∞ .

Teraz sa pozrime na to, ako nájsť rozsah funkcie, ktorá nie je spojitá. Aby sme to dosiahli, musíme rozdeliť celú oblasť na intervaly a nájsť sady hodnôt na každom z nich a potom skombinovať to, čo sme dostali. Aby ste tomu lepšie porozumeli, odporúčame vám prečítať si hlavné typy bodov prerušenia funkcií.

Príklad 11

podmienka: daná funkcia y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3. Vypočítajte jeho rozsah.

Riešenie

Táto funkcia je definovaná pre všetky hodnoty x. Analyzujme to z hľadiska kontinuity s hodnotami argumentu rovnými - 3 a 3:

lim x → - 3 - 0 f (x) = lim x → - 3 2 hriech x 2 - 4 = 2 hriech - 3 2 - 4 = - 2 hriech 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)

Máme neobnoviteľnú diskontinuitu prvého druhu s hodnotou argumentu -3. Keď sa k nej priblížite, hodnoty funkcie budú mať tendenciu k -2 sin 3 2 - 4 a keď sa x na pravej strane priblíži k -3, hodnoty budú mať tendenciu k -1.

lim x → 3 - 0 f(x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f(x) = lim x → 3 + 0 1 x - 3 = + ∞

V bode 3 máme neodstrániteľnú diskontinuitu druhého druhu. Keď k tomu funkcia smeruje, jej hodnoty sa približujú - 1, pričom smerujú k rovnakému bodu vpravo - k mínus nekonečnu.

To znamená, že celý definičný obor tejto funkcie je rozdelený na 3 intervaly (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .

Na prvom z nich sme dostali funkciu y \u003d 2 sin x 2 - 4. Keďže - 1 ≤ sin x ≤ 1 , dostaneme:

1 ≤ hriech x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

To znamená, že na tomto intervale (- ∞ ; - 3 ] je množina hodnôt funkcie [ - 6 ; 2 ] .

Na polovičnom intervale (- 3 ; 3 ] dostaneme konštantnú funkciu y = - 1 . Následne sa celá množina jej hodnôt v tomto prípade zredukuje na jedno číslo - 1 .

Na druhom intervale 3; + ∞ máme funkciu y = 1 x - 3 . Klesá, pretože y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Množina hodnôt pôvodnej funkcie pre x > 3 je teda množina 0 ; +∞ . Teraz spojme výsledky: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0; +∞ .

odpoveď: E(y) = -6; - 2 ∪ - 1 ∪ 0; +∞ .

Riešenie je znázornené v grafe:

Príklad 12

Podmienka: existuje funkcia y = x 2 - 3 e x . Určte množinu jeho hodnôt.

Riešenie

Je definovaný pre všetky hodnoty argumentov, ktoré sú skutočnými číslami. Určme, v akých intervaloch sa bude táto funkcia zvyšovať a v akých klesá:

y "= x 2 - 3 e x" = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

Vieme, že derivácia bude 0, ak x = -1 a x = 3 . Tieto dva body umiestnime na os a zistíme, aké znamienka bude mať derivácia na výsledných intervaloch.

Funkcia sa zníži o (- ∞ ; - 1 ] ∪ [ 3 ; + ∞ ) a zvýši o [ - 1 ; 3]. Minimálny bod bude -1, maximálny -3.

Teraz nájdime zodpovedajúce hodnoty funkcií:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

Pozrime sa na správanie funkcie v nekonečne:

lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 "e x" = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x "(e x)" = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0

Na výpočet druhého limitu sa použilo L'Hopitalovo pravidlo. Nakreslime naše riešenie do grafu.

Ukazuje, že hodnoty funkcie sa znížia z plus nekonečna na -2 e, keď sa argument zmení z mínus nekonečna na -1. Ak sa zmení z 3 na plus nekonečno, hodnoty sa znížia z 6 e - 3 na 0, ale 0 sa nedosiahne.

Teda E(y) = [-2e; +∞).

odpoveď: E (y) = [-2e; +∞)

Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter