D(f)- te wartości, które może przyjąć argument, tj. zakres funkcji.

mi(f)- te wartości, które może przyjąć funkcja, tj. zbiór wartości funkcji.

Metody znajdowania zakresów funkcji.

sekwencyjne znajdowanie wartości złożonych argumentów funkcji;

metoda punktowa/graniczna;

wykorzystanie własności ciągłości i monotoniczności funkcji;

użycie instrumentu pochodnego;

używając największych i najmniejszych wartości funkcji;

metoda graficzna;

metoda wprowadzania parametrów;

metoda funkcji odwrotnej.

Rozważmy niektóre z nich.

Korzystanie z pochodnej

Ogólne podejście znalezienie zbioru wartości funkcji ciągłej f(x) polega na znalezieniu największej i najmniejszej wartości funkcji f(x) w jej dziedzinie (lub udowodnieniu, że jedna lub obie nie istnieją) .

Jeśli potrzebujesz znaleźć zestaw wartości funkcji na segmencie:

znajdź pochodną danej funkcji f "(x);

znajdź punkty krytyczne funkcji f(x) i wybierz te, które należą do danego odcinka;

obliczyć wartości funkcji na końcach odcinka iw wybranych punktach krytycznych;

spośród znalezionych wartości wybierz najmniejszą i największą wartość;

Zestaw wartości funkcji jest zawarty między tymi wartościami.

Jeśli zakres funkcji jest interwał, wówczas używany jest ten sam schemat, ale zamiast wartości na końcach stosowane są granice funkcji, gdy argument zmierza do końca przedziału. Wartości graniczne od nie są uwzględnione w zestawie wartości.

Metoda graniczna/wynikowa

Aby znaleźć zestaw wartości funkcji, najpierw znajdź zestaw wartości argumentów, a następnie znajdź odpowiednie wartości minimalne i maksymalne funkcji funkcji. Korzystając z nierówności - wyznacz granice.

Istotą jest oszacowanie funkcji ciągłej z dołu i z góry oraz udowodnienie, że funkcja osiąga dolną i górną granicę oszacowań. W tym przypadku zbieżność zbioru wartości funkcji z przedziałem od dolnej granicy oszacowania do górnej jest określona przez ciągłość funkcji i brak dla niej innych wartości.

Własności funkcji ciągłej

Inną opcją jest przekształcenie funkcji w ciągłą funkcję monotoniczną, następnie wykorzystując właściwości nierówności szacuje się zbiór wartości nowo otrzymanej funkcji.

Sekwencyjne znajdowanie wartości argumentów funkcji złożonych

Oparte na sekwencyjnym wyszukiwaniu zbioru wartości funkcji pośrednich, które składają się na funkcję

Przedziały podstawowych funkcji elementarnych

Funkcjonować	Wiele wartości
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^(2n)$	E(y) =
$y = \cos(x)$	E(y) = [-1;1]
$y = (\rmtg)\, x$	E(y) = (-∞;+∞)
$y = (\rm ctg)\, x$	E(y) = (-∞;+∞)
$y = \arcsin(x)$	E(y) = [-π/2; π/2]
$y = \arccos(x)$	E(y) =
$y = (\rm arctg)\, x$	E(y) = (-π/2; π/2)
$y = (\rm arcctg)\, x$	E(y) = (0; π)

Przykłady

Znajdź zbiór wartości funkcji:

Korzystanie z pochodnej

Znajdź dziedzinę definicji: D(f)=[-3;3], ponieważ $9-x^(2)\geq 0$

Znajdź pochodną: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0, jeśli x = 0. f"(x) nie istnieje, jeśli $\sqrt(9-x^(2))=0$, tj. dla x = ±3. Otrzymujemy trzy punkty krytyczne: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, z których dwa pokrywają się z końcami odcinka. Oblicz: f(–3) = 0, f(0) = 3, f(3) = 0. Zatem najmniejsza wartość f(x) to 0, największa to 3.

Odpowiedź: E(f) = .

NIE używając pochodnej

Znajdź największą i najmniejszą wartość funkcji:

Od $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , wtedy:

$f(x)\leq \frac(3)(4)$ dla wszystkich x;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ dla wszystkich x(ponieważ $|\cos (x)|\równik 1$);

$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;

$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

Odpowiedź: $\frac(3)(4)$ i $-\frac(3)(2)$

Jeśli rozwiążesz ten problem za pomocą pochodnych, będziesz musiał pokonać przeszkody związane z faktem, że funkcja f (x) jest zdefiniowana nie na odcinku, ale na całej linii rzeczywistej.

Korzystanie z metody granic/szacunków

Z definicji sinusa wynika, że ​​$-1\leq\sin(x)\leq 1$. Następnie korzystamy z własności nierówności liczbowych.

$-4\leq - 4\sin(x)\leq 4$, (pomnóż wszystkie trzy części podwójnej nierówności przez -4);

$1\leq 5 - 4\sin(x)\leq 9$ (dodane do trzech części podwójnej nierówności 5);

Ponieważ ta funkcja jest ciągła w całej dziedzinie definicji, zbiór jej wartości leży między jej najmniejszą a największą wartością w całej dziedzinie definicji, jeśli taka istnieje.

W tym przypadku zbiorem wartości funkcji $y = 5 - 4\sin(x)$ jest zbiór .

Z nierówności $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ otrzymujemy oszacowanie $$\\ -6\leq y\ leq 6 $ $

Dla x = p i x = 0 funkcja przyjmuje wartości -6 i 6, tj. osiąga dolną i górną granicę. Jako liniowa kombinacja funkcji ciągłych cos(7x) i cos(x), funkcja y jest ciągła wzdłuż całej osi liczbowej, dlatego przez właściwość funkcji ciągłej przyjmuje wszystkie wartości od -6 do 6 włącznie , i tylko one, ponieważ ze względu na nierówności $- 6\leq y\leq 6$ inne wartości są dla niego niemożliwe.

Dlatego E(y) = [-6;6].

$$ \\ -1\równoważnik\sin(x)\równoważnik 1 \\ 0\równoważnik\sin^(2)(x)\równoważnik 1 \\ 0\równoważnik2\sin^(2)(x)\równoważnik 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Odpowiedź: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Przekształćmy wyrażenie $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.

Definicja cosinusa implikuje $$ \\ -1\leq\cos(x)\leq 1; \\ -1\równik \cos((x + \frac(\pi)(4)))\równik 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

Ponieważ funkcja ta jest ciągła na całej dziedzinie definicji, to zbiór jej wartości jest zawarty między jej najmniejszą a największą wartością, jeśli taka występuje, zbiorem wartości funkcji $y =\sqrt(2)\ cos((x +\frac(\pi)(4 )))$ to zbiór $[-\sqrt(2);\sqrt(2)]$.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

Oznaczmy $t = 5 – (3^(x)+1)^(2)$, gdzie -∞≤t≤4. Tym samym problem sprowadza się do znalezienia zbioru wartości funkcji $y = \log_(0,5)(t)$ na półprostej (-∞;4). Ponieważ funkcja $y = \log_(0,5)(t)$ jest zdefiniowana tylko dla t > 0 , to jej zbiór wartości na półprostej (-∞;4) pokrywa się ze zbiorem wartości funkcja na przedziale (0;4) reprezentująca przecięcie promienia (-∞;4) z dziedziną definicji (0;+∞) funkcji logarytmicznej. Na przedziale (0;4) funkcja ta jest ciągła i malejąca. Dla t > 0 dąży do +∞, a dla t = 4 przyjmuje wartość -2, więc E(y) = (-2, +∞).

Stosujemy technikę opartą na graficznym przedstawieniu funkcji.

Po przekształceniach funkcji mamy: y 2 + x 2 = 25, oraz y ≥ 0, |x| ≤ 5.

Należy przypomnieć, że $x^(2)+y^(2)=r^(2)$ jest równaniem okręgu o promieniu r.

Przy tych ograniczeniach wykresem tego równania jest górne półkole o środku w początku układu współrzędnych i promieniu równym 5. Jest oczywiste, że E(y) = .

Odpowiedź: E(y) = .

Bibliografia

Zakres funkcji w zadaniach Jednolitego Egzaminu Państwowego, Minyuk Irina Borisovna

Wskazówki dotyczące znajdowania zestawu wartości funkcji, Belyaeva I., Fedorova S.

Znajdowanie zbioru wartości funkcji

Jak rozwiązywać problemy z matematyki na egzaminach wstępnych, I.I. Melnikov, I.N. Sergeev

Liceum GBOU (ekonomiczne) z. Izakla

Nauczyciel matematyki Kuzaeva V.N.

2016

Materiały referencyjne

Próbka rozwiązania Znajdź zestaw wartości funkcji

Zakres funkcji
jest

y - Jakikolwiek numer

Zakres funkcji
jest y - Jakikolwiek numer

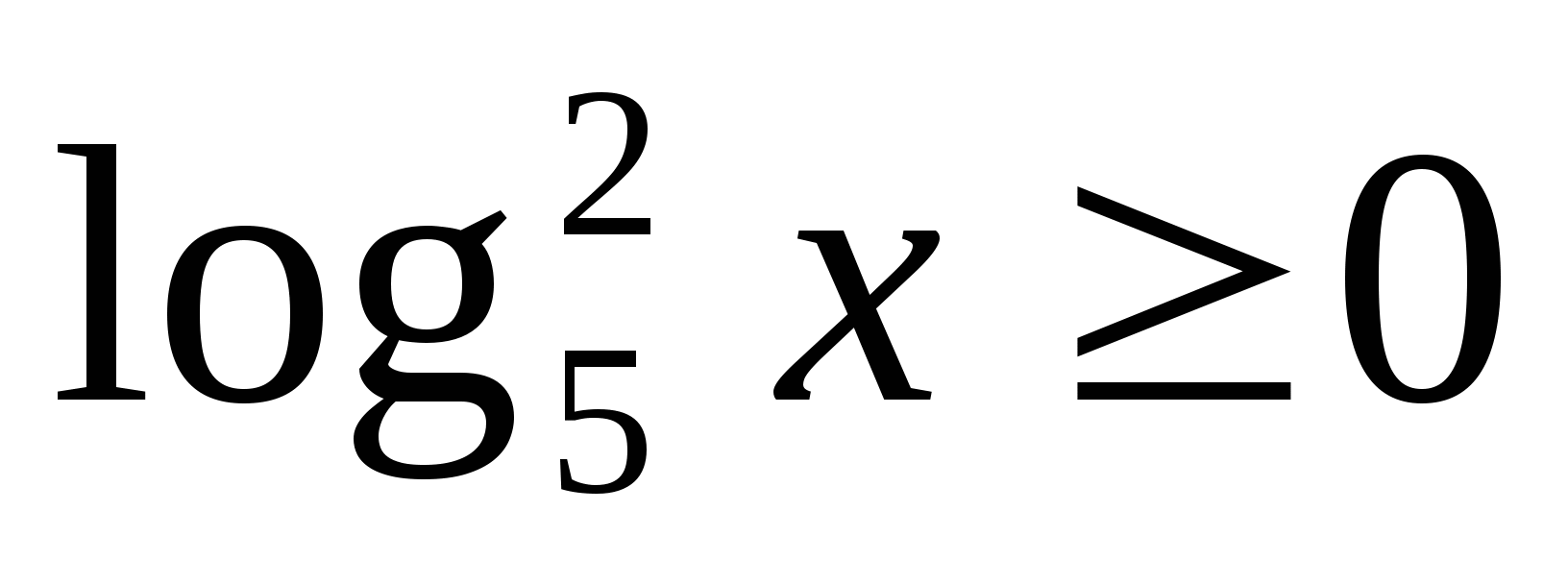
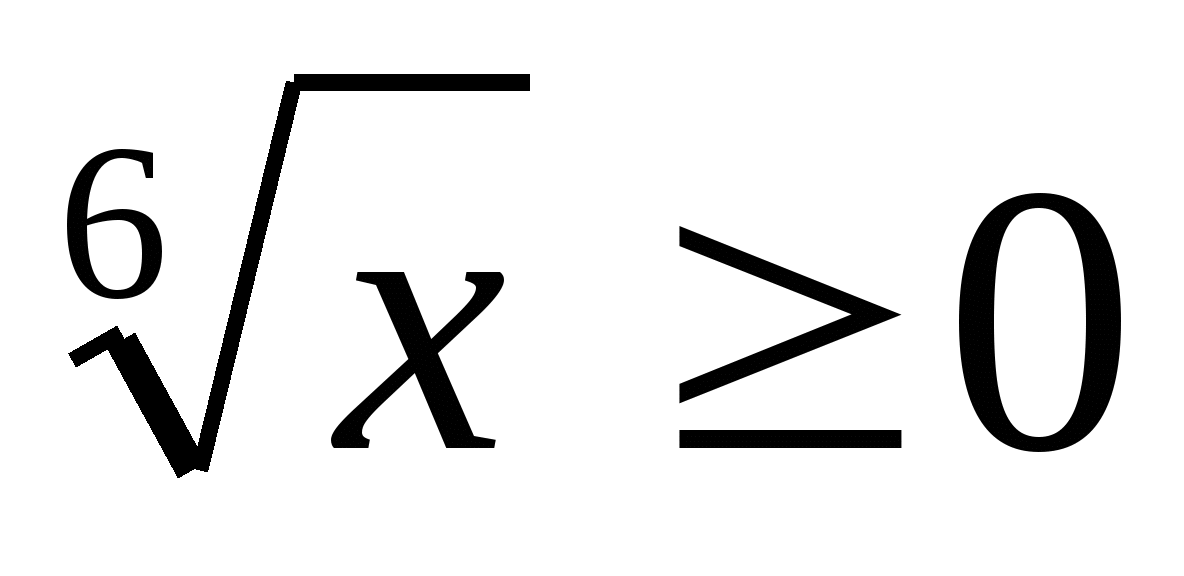
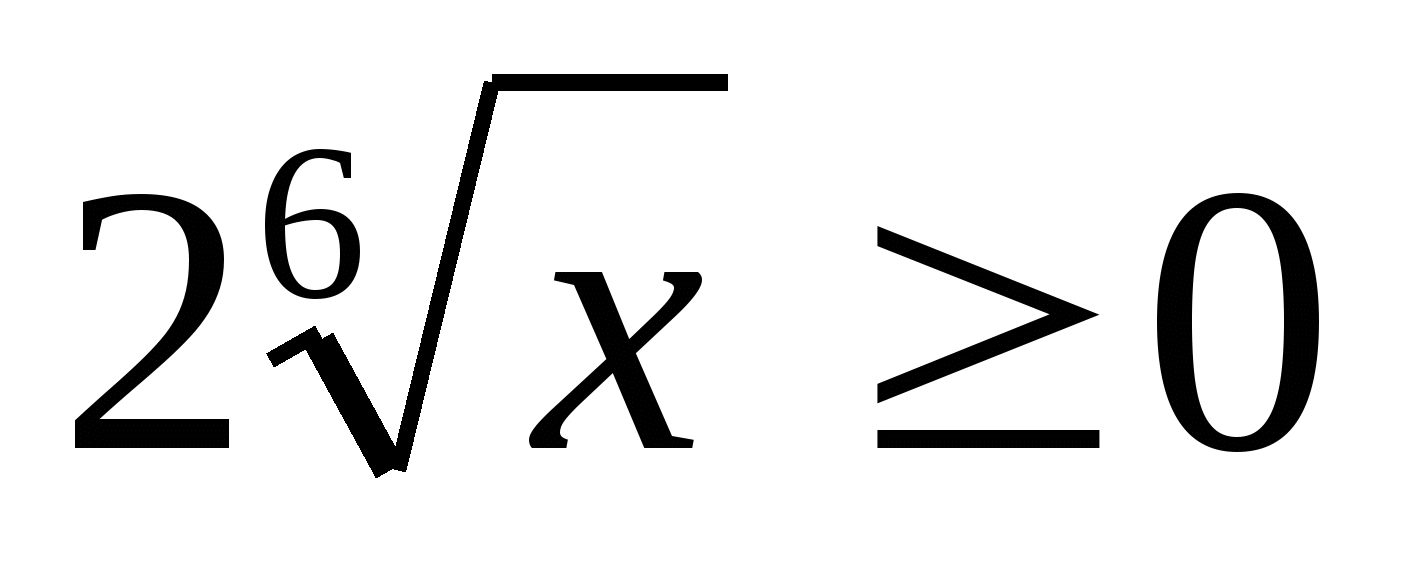
Wiele wartości

y - Jakikolwiek numer

Najwyższa wartość

Najniższa wartość

Domena X - Jakikolwiek numer
, gdzie

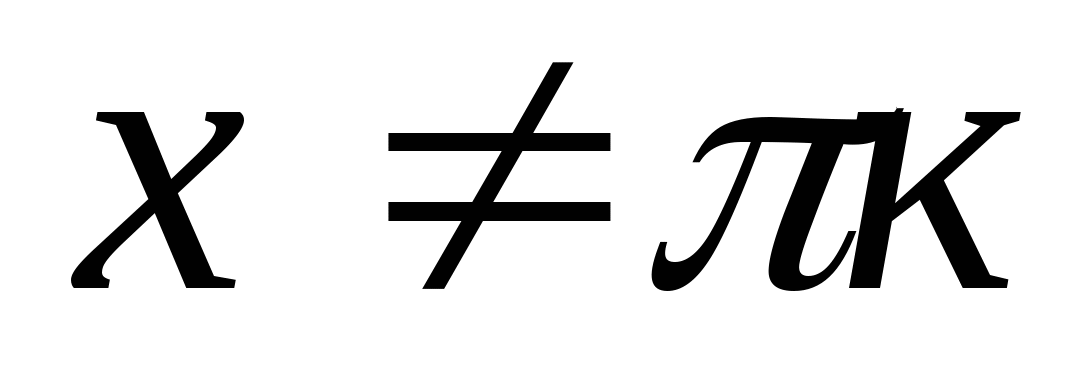, gdzie

Wiele wartości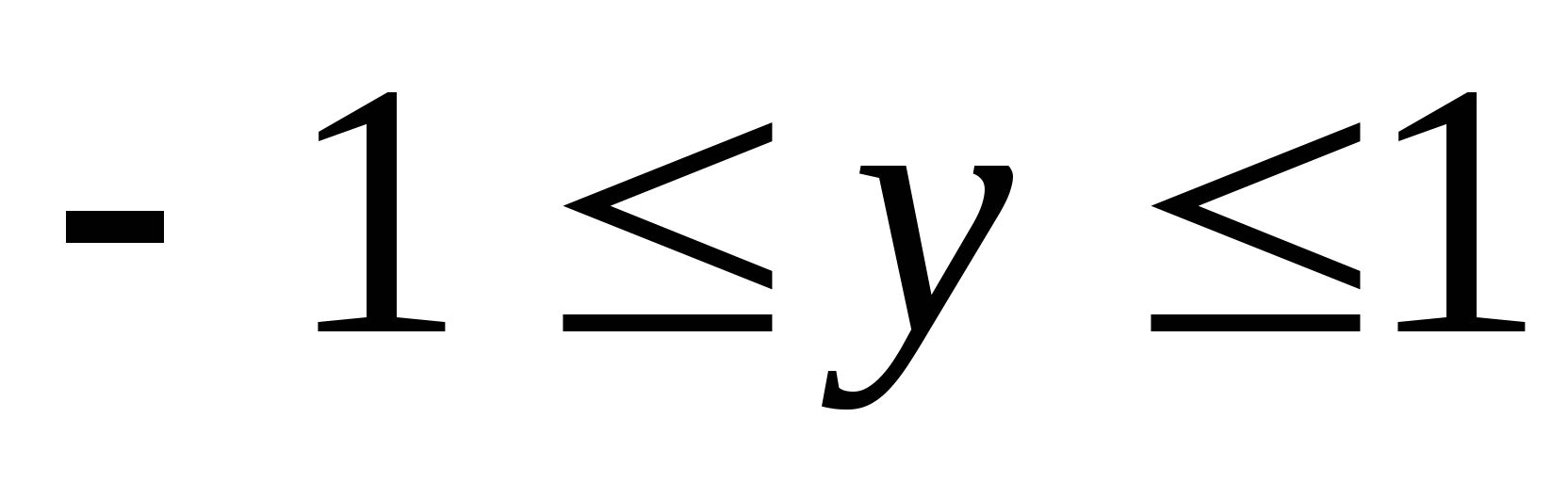
y - Jakikolwiek numery - Jakikolwiek numer

Szablony wykresów dla niektórych funkcji trygonometrycznych

Zestaw wartości funkcji trygonometrycznych

opcja 1

Y =grzech 3x+2.

1) (-5;5) 2) 3) 4) (1;5)

2. Znajdź obszar funkcji y =tg x + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. Podaj najmniejszą liczbę całkowitą z zakresu funkcji

y = 12,7 + 5 grzech(3x-2).

1) -5 2) 8 3) 5 4) 17

5. Podaj funkcję, której zbiorem wartości jest odcinek [-2;2].

1) y = sałata 2x 2) y = grzech 2 x 3) y = sałata 2 x +2

4) y = 2 grzech 4 x

6. Znajdź zbiór wartości funkcjiy = tg 2 xna segmencie

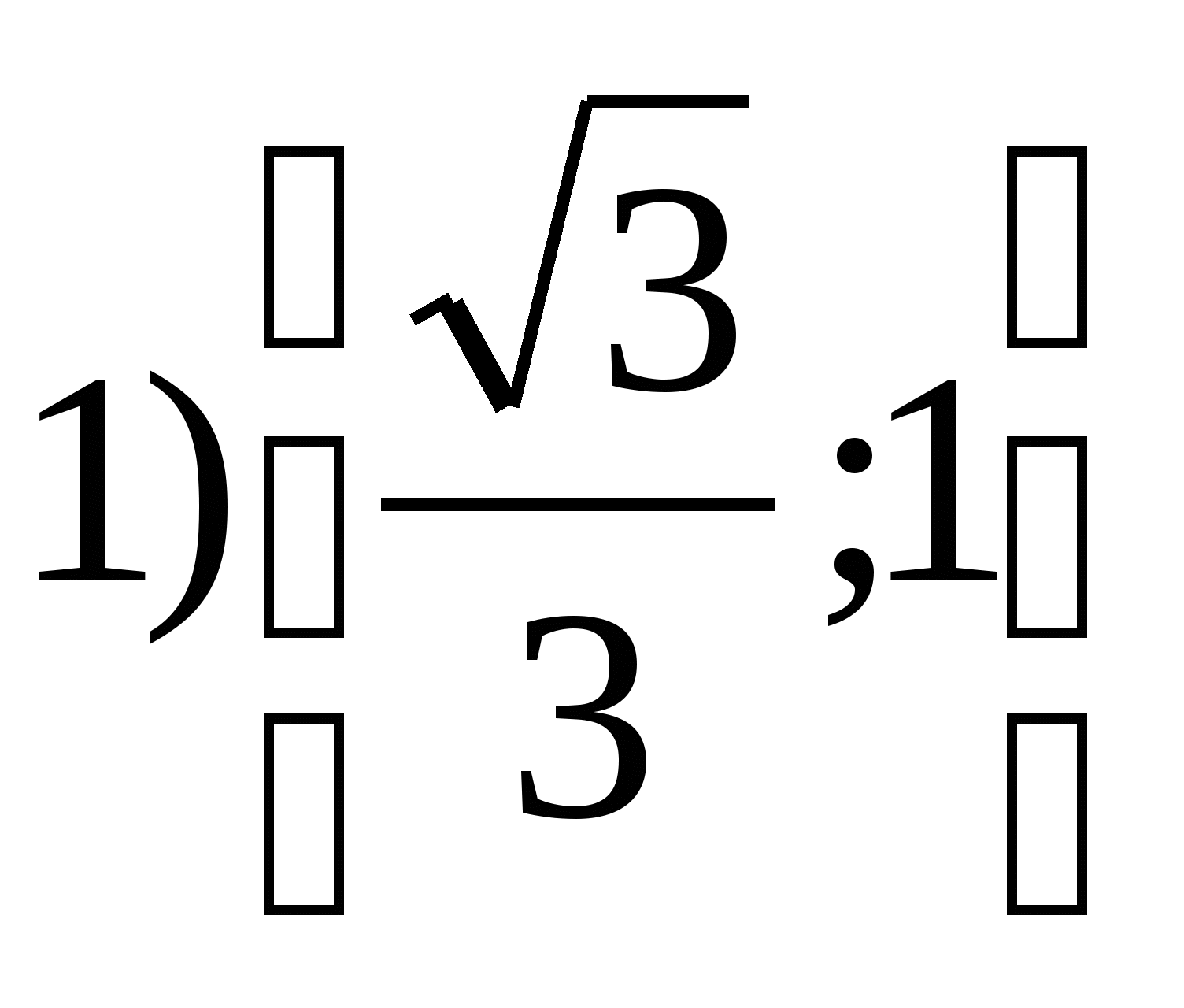
7. Znajdź sumę wszystkich liczb całkowitych, które mieszczą się w zakresie funkcjiy = 4 sałata 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Opcja 2

y = 2 sałata 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Znajdź zakres funkcji

1) 3) (-∞;∞) 4) .

3. Podaj najmniejszą liczbę z zakresu funkcji

1) 4 2) -3 3) 1 4) -7

4. Podaj największą liczbę całkowitą z zakresu funkcji

1) 2 2) 13 3) 12 4) -2

5. Podaj funkcję, której zbiorem wartości jest odcinek [-5;5].

1) y = grzech 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = grzech 5x + 5

6. Znajdź zbiór wartości funkcji
na segmencie

7. Znajdź iloczyn wszystkich liczb całkowitych mieszczących się w zakresie funkcji y \u003d 5 - 3grzech 2 x.

1) 120 2) 14 3) -15 4) 0

Opcja 3
1. Określ zestaw wartości funkcjiy = grzech 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Podaj najmniejszą liczbę z zakresu funkcji y = 5tg 2 x+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Określ funkcję, której zestawem wartości jest segment

[-17;-13].

1) y \u003d 5 grzech x - 8 3) y \u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 grzech x +10

6. Wskaż najmniejszą liczbę naturalną, która nie należy do zbioru wartości funkcji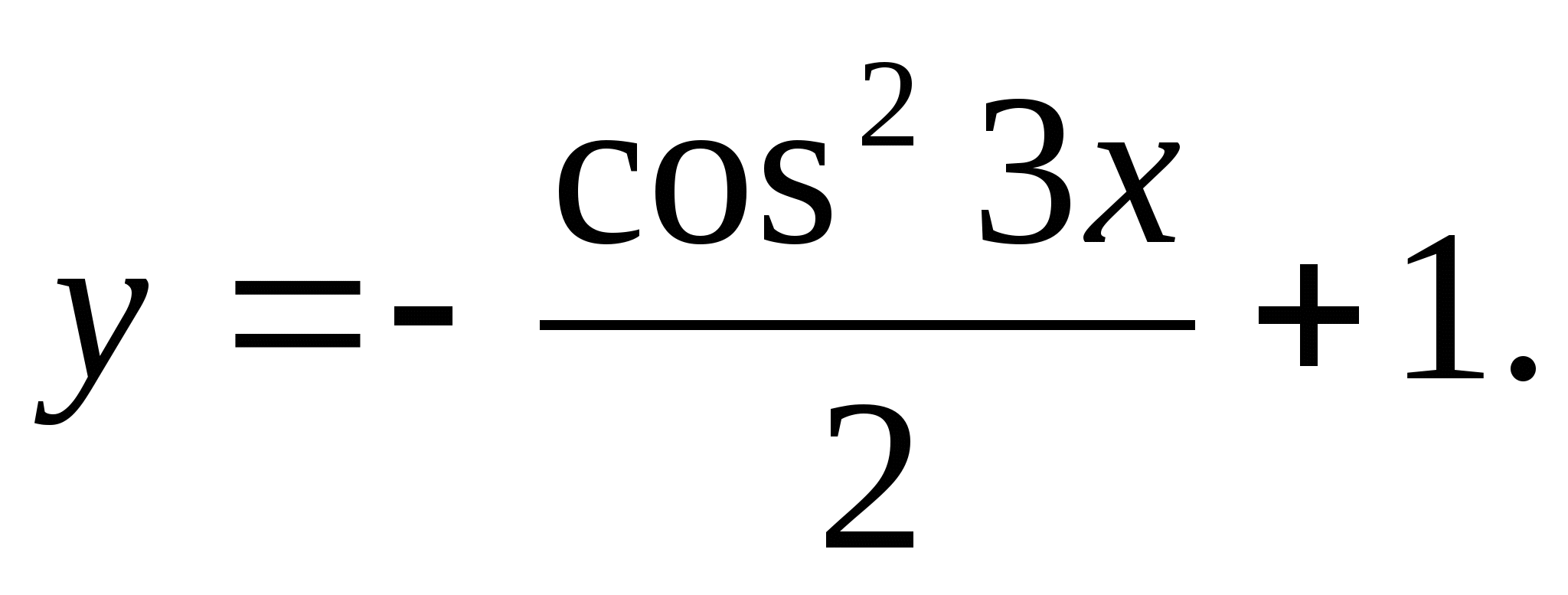

1) 2 2) 4 3) 15 4) 6

7. Ile liczb całkowitych należy do zbioru wartości funkcji

y = 2 sałata 3 x +10?

1) 2 2) 3 3) 4 5) 5

Opcja 4

1) 2) 4) (-7;-6)

2. Znajdź zakres funkcji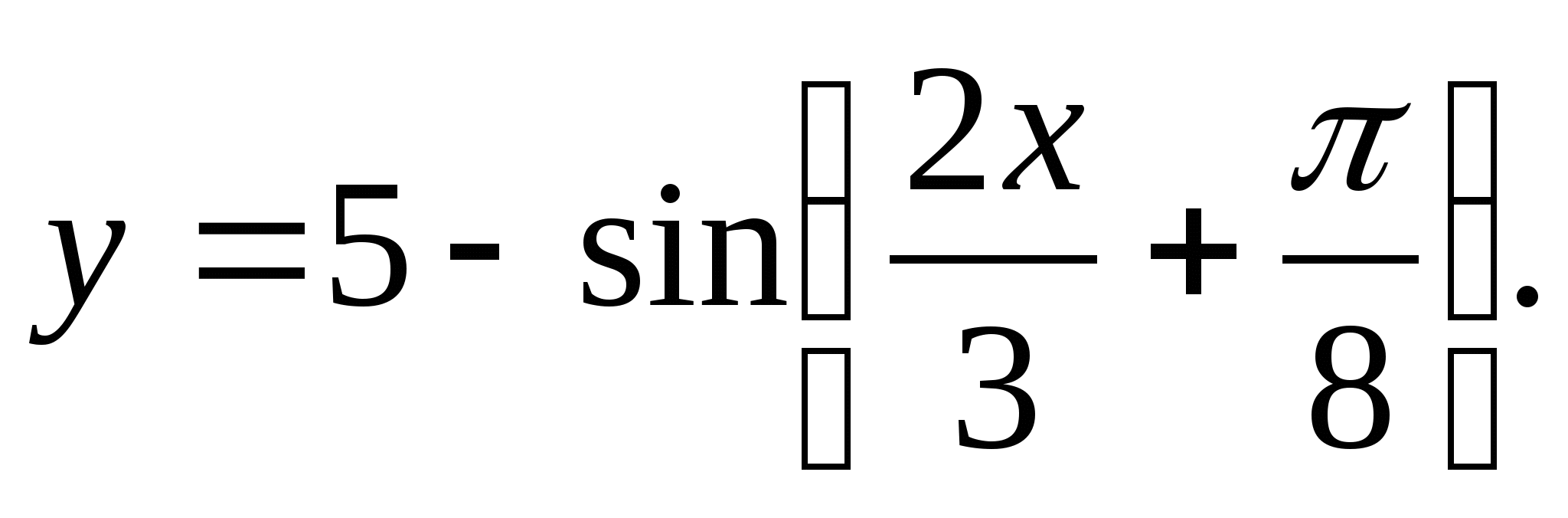

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Podaj największą liczbę z zakresu funkcjiy = -3 ktg 2 x+7.

1) 10 2) 4 3) 7 4) -3

4. Która z poniższych liczb nie należy do zbioru wartości funkcji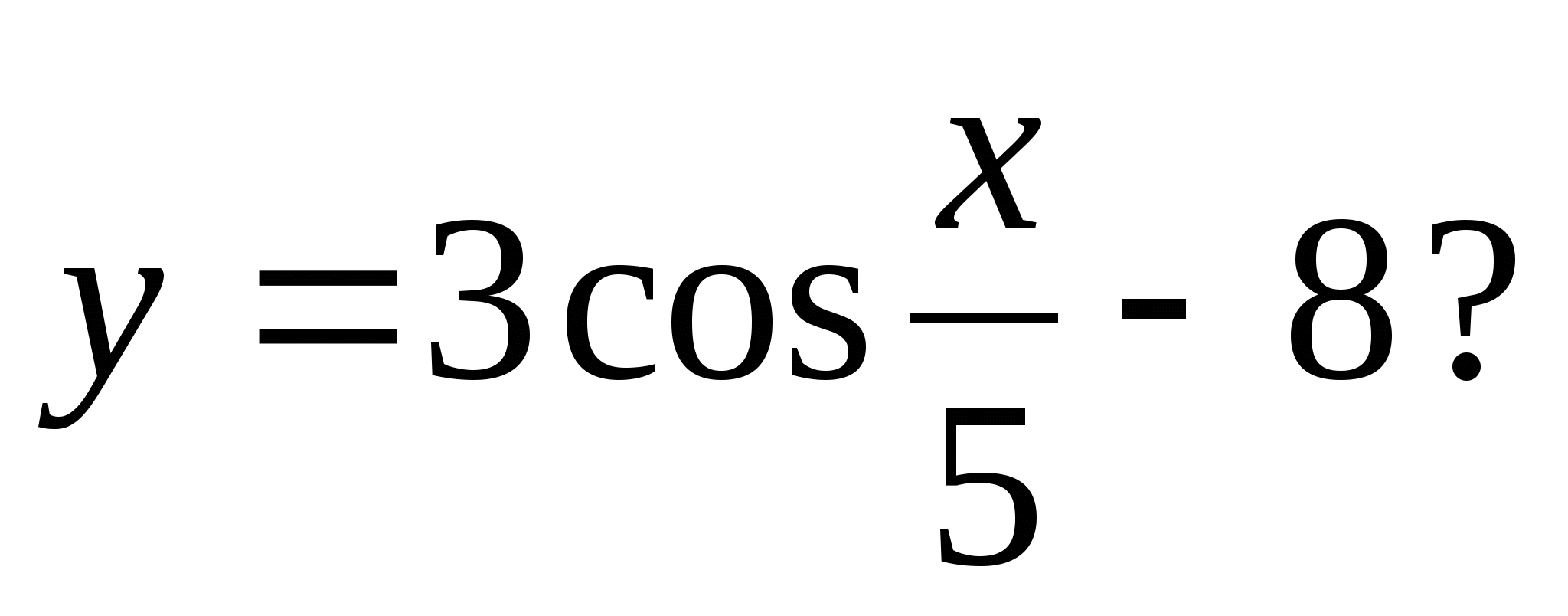

1) -6 2) -5 3) -10 4) -7

5. Określ funkcję, której zbiorem wartości jest przedział.

6. Podaj największą ujemną liczbę całkowitą, która nie mieści się w zakresie funkcji

1) -1 2) -25 3) -6 4) -2

7. Ile liczb całkowitych należy do zbioru wartości funkcji

1) 11 2) 3 3) 5 4) 4

Opcja 5

1. Określ zestaw wartości funkcji y = 2 -grzech 5 x.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Znajdź zakres funkcji

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Podaj najmniejszą liczbę całkowitą z zakresu funkcji

y = 3 + grzech 2 2 x.

1) 0 2) 1 3) 3 4) 4

4. Która z poniższych liczb należy do zbioru wartości funkcji

1) 128 2) 10,5 3) 3 4) -235

5. Podaj funkcję, której zbiorem wartości jest odcinek [-9;15].

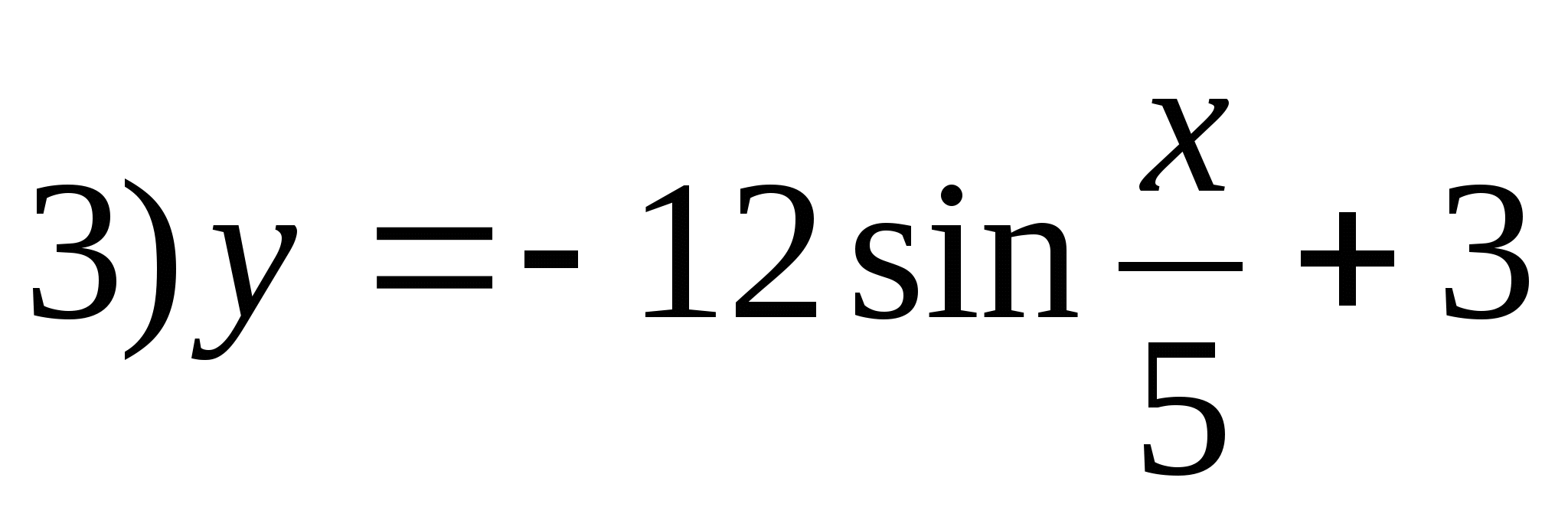
6. Znajdź sumę liczb całkowitych wchodzących w skład zbioru wartości funkcji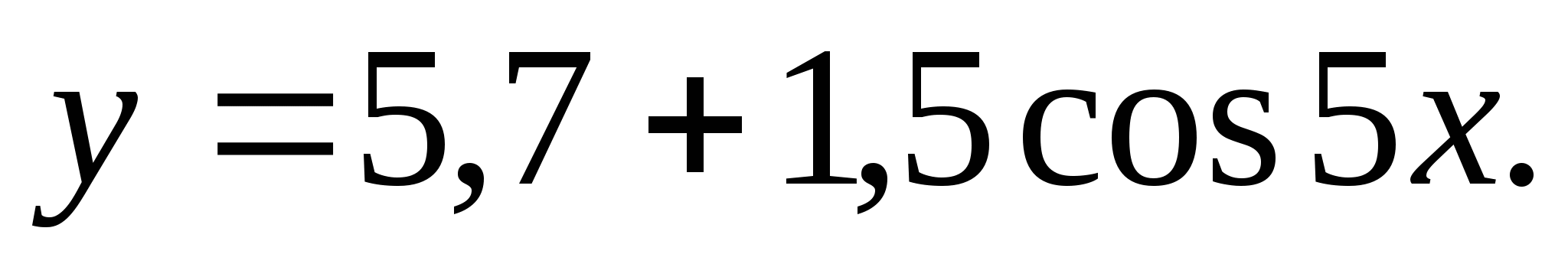

1) 0 2) 7 3) 18 4) 22

7. Znajdź największą wartość funkcji
na segmencie

1) 0,5 2) 1,5 3) 0 4) 2

Opcja 6

1. Określ segment odpowiadający zbiorowi wartości funkcji

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Znajdź zakres funkcji

3. Podaj największą liczbę z zakresu funkcji

1) 5 2) -6 3) -3 4) 4

4. Która z poniższych liczb należy do zbioru wartości funkcji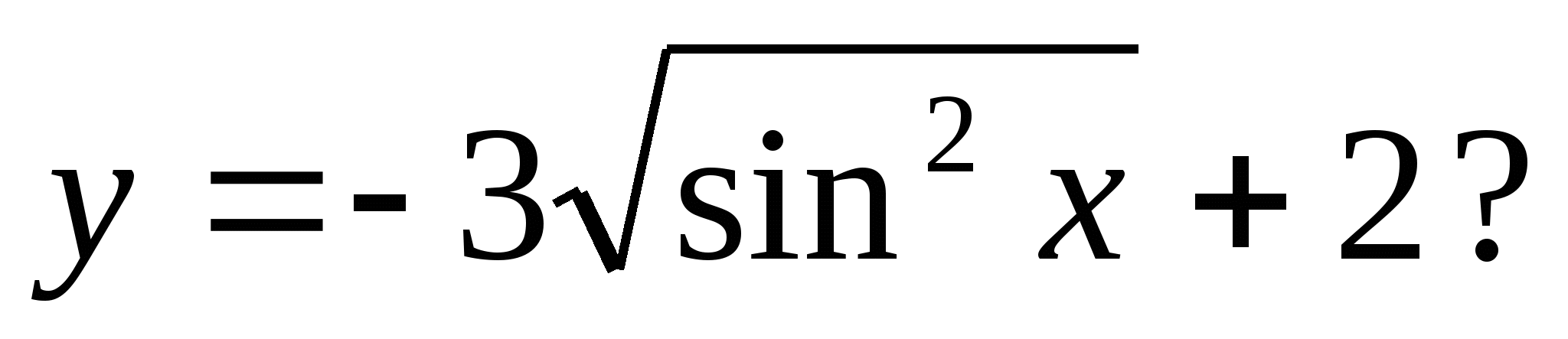

1) 5 2) 0 3) -3 4) 4

5. Określ funkcję, której zbiorem wartości jest przedział.

1) w = 15 – 7 sałata 2x 3) y = 7 sałata 2x + 3

2) y = 5 sałata 4 x 4) y = - tg 2 x + 1

6. Znajdź iloczyn liczb całkowitych zawartych w zbiorze wartości

y = 3,8 – 1,4 grzech 3 x.

1) 17 2) 12 3) 0 4) 60

7. Znajdź zbiór wartości funkcji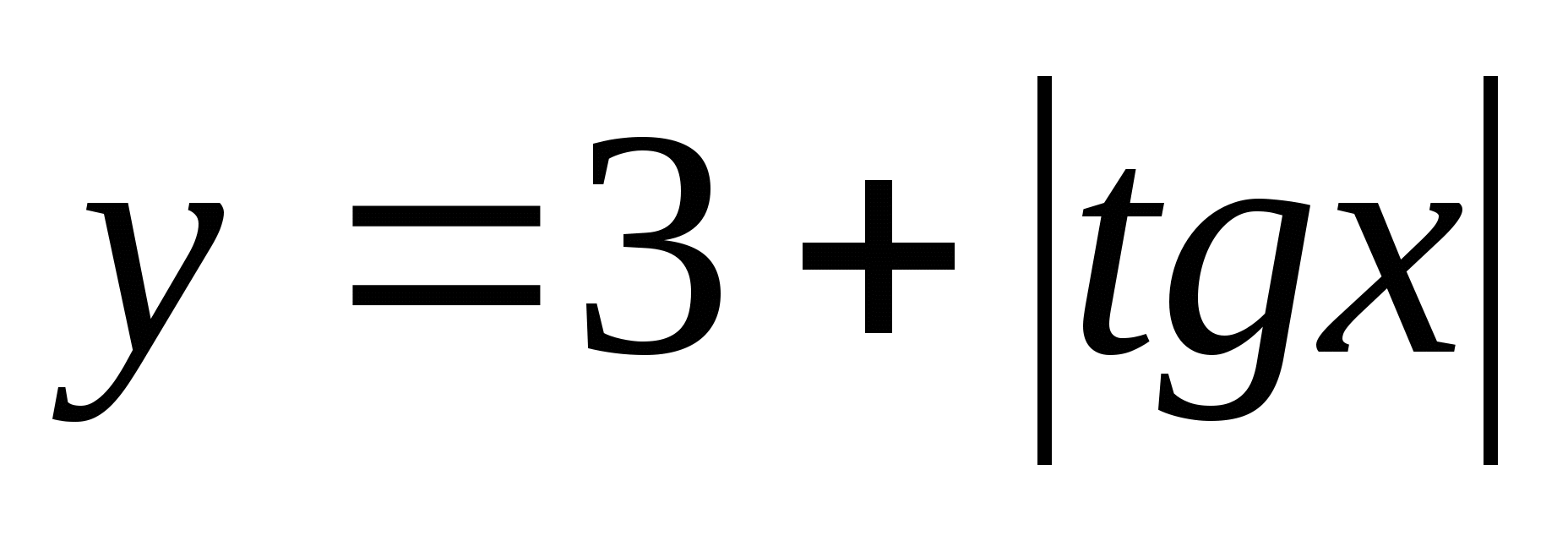
pomiędzy

1) (3;4) 2) 3)

Opcja 7

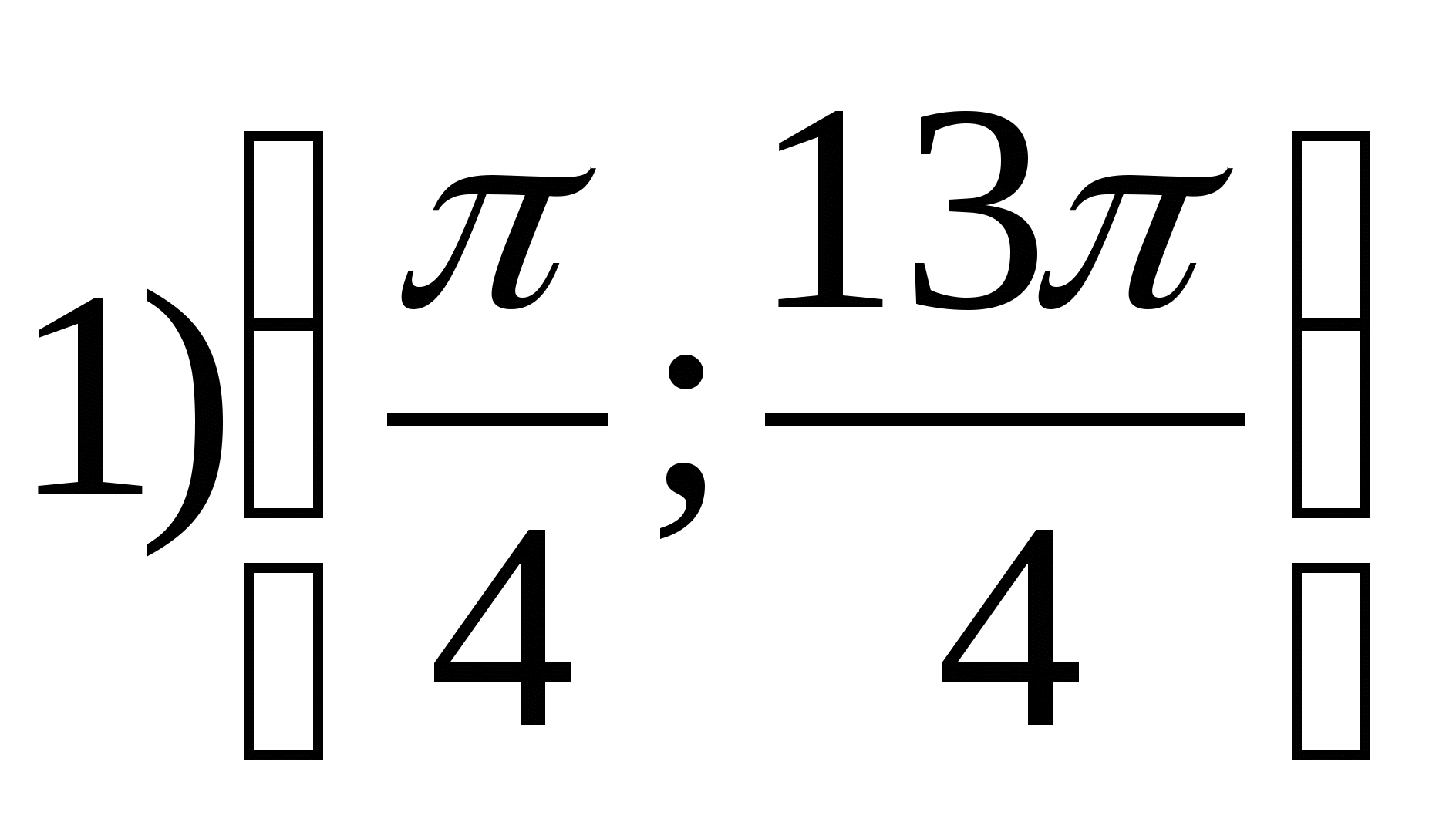
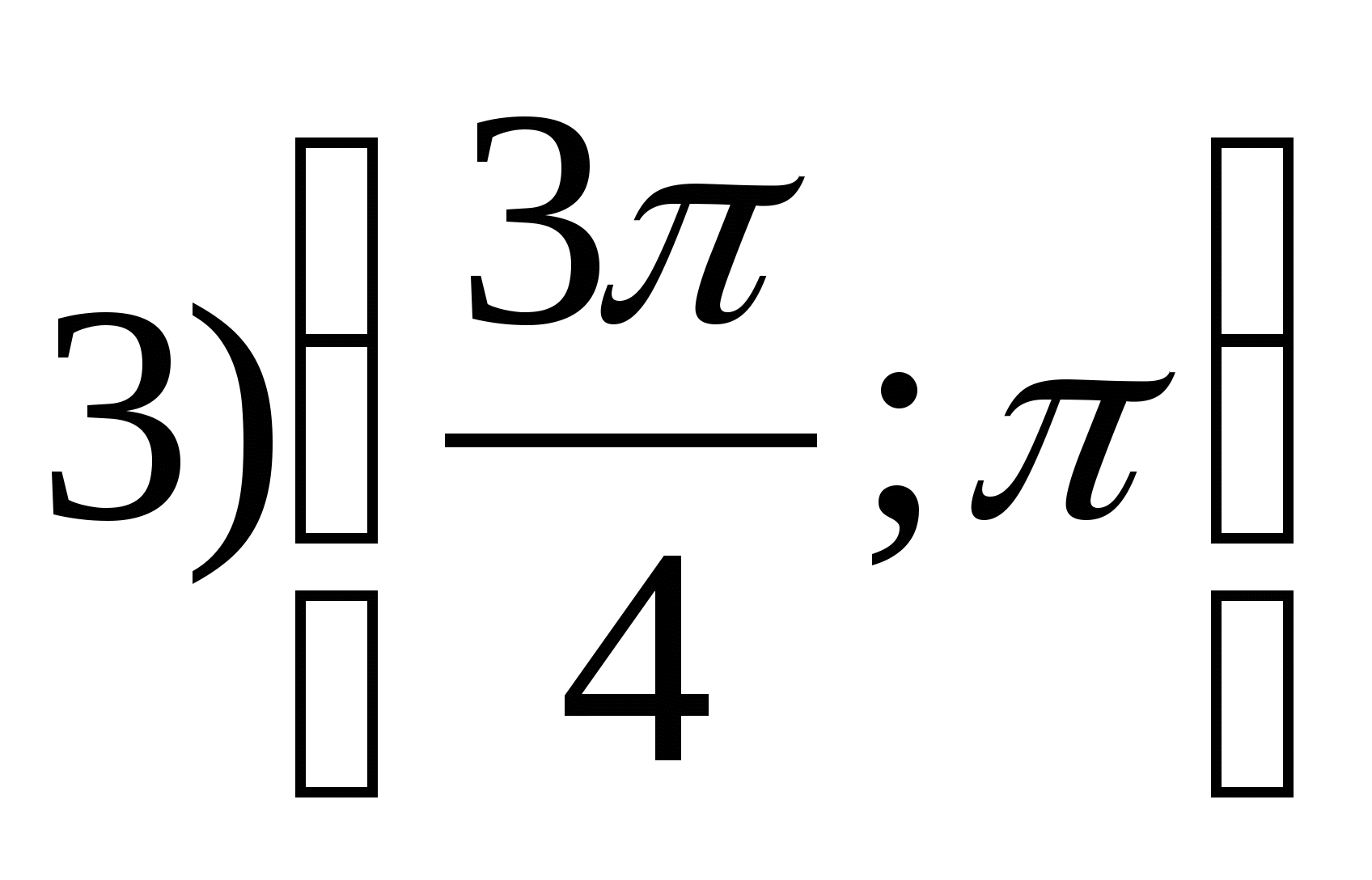
2. Znajdź najmniejszą całkowitą wartość funkcji

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. Dla jakich wartości a robi równaniegrzech(3 x-4)+5= a rozpuszczalny?

1) 2) 3) (4;6) 4) (-6;4]

grzech 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

pomiędzy

2) 0 3) 1

y = 4 grzech(x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Opcja 8

1. Znajdź zbiór wartości funkcjiy = arctgx- 2π.

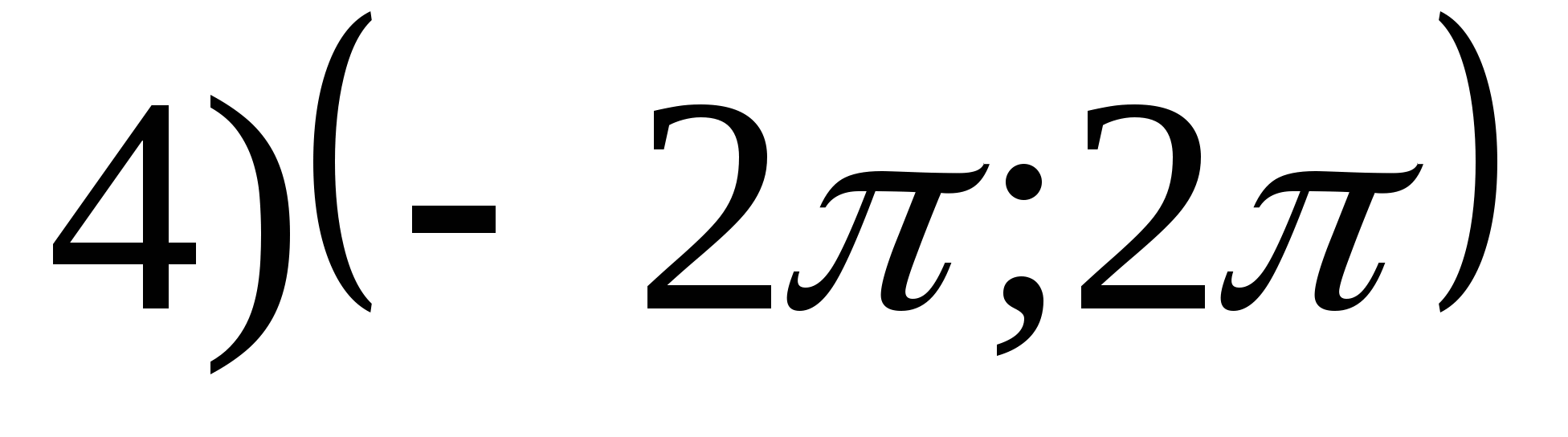
2. Znajdź największą wartość funkcji

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Która z poniższych liczb może być wartością funkcji

1) -4 2) -2 3) 0 4) 2

4. Dla jakich wartości równania p -2+sałata(4 x-1)= p ma korzenie?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Znajdź zbiór wartości funkcjiy = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

pomiędzy
.

1) 0 2) 1 3) -1 4) 3

7. Ile liczb całkowitych mieści się w przedziale funkcji

1) 4 2) 3 3) 5 4) 2

Opcja 9

1. Znajdź zakres funkcji

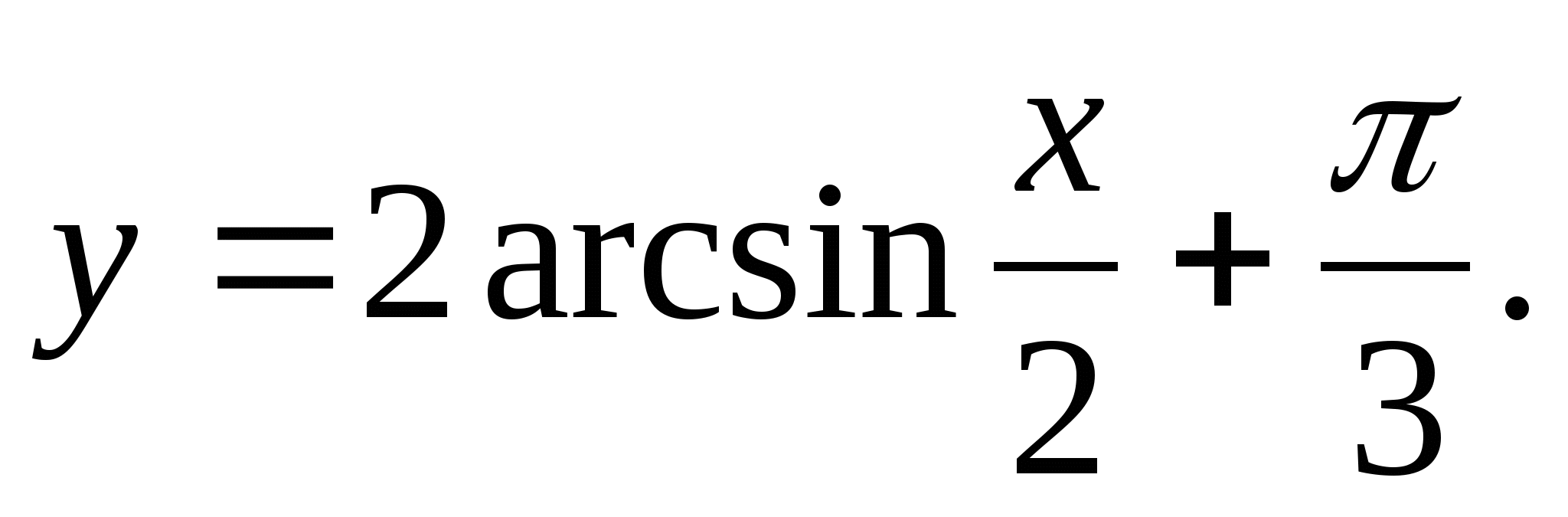
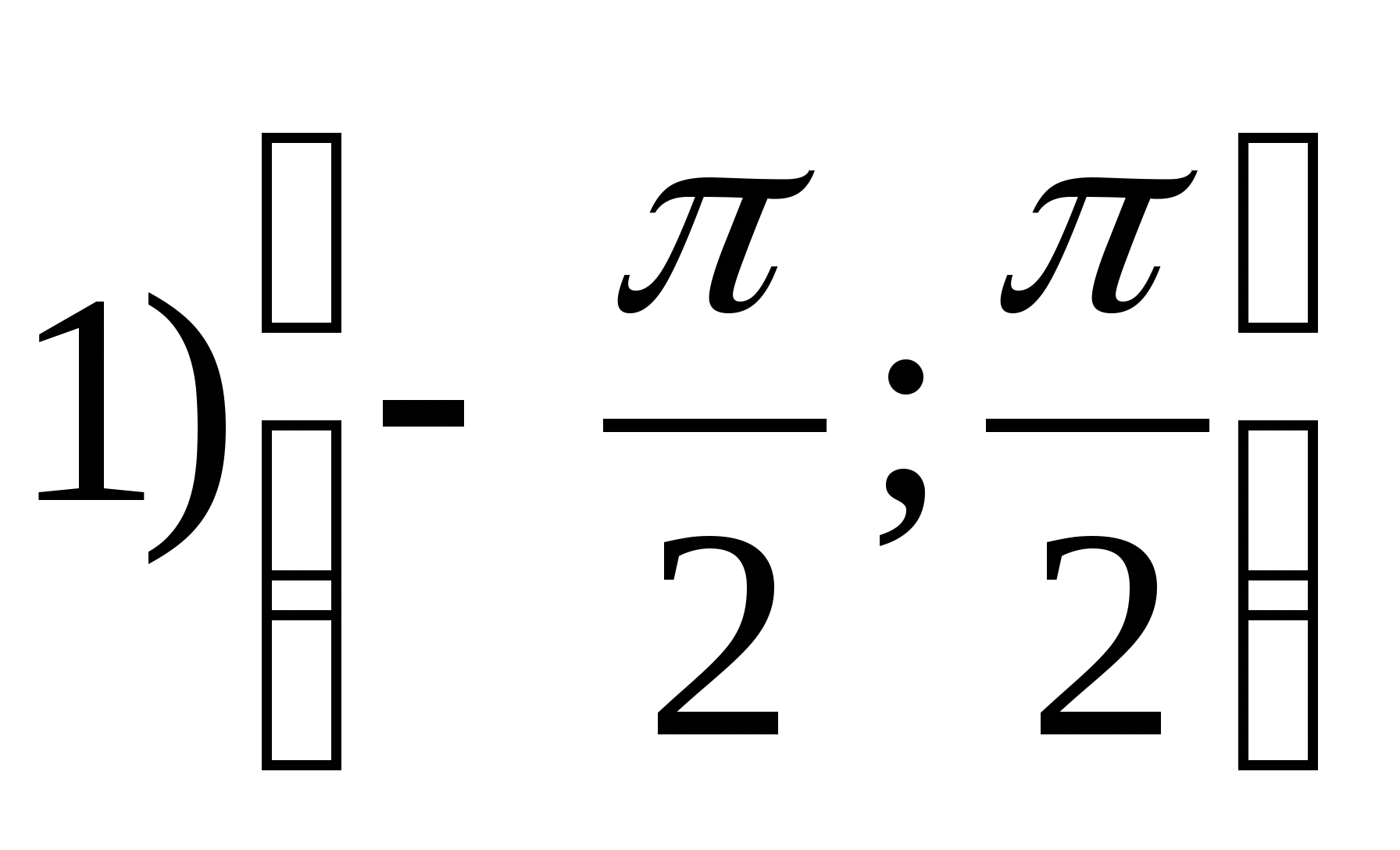
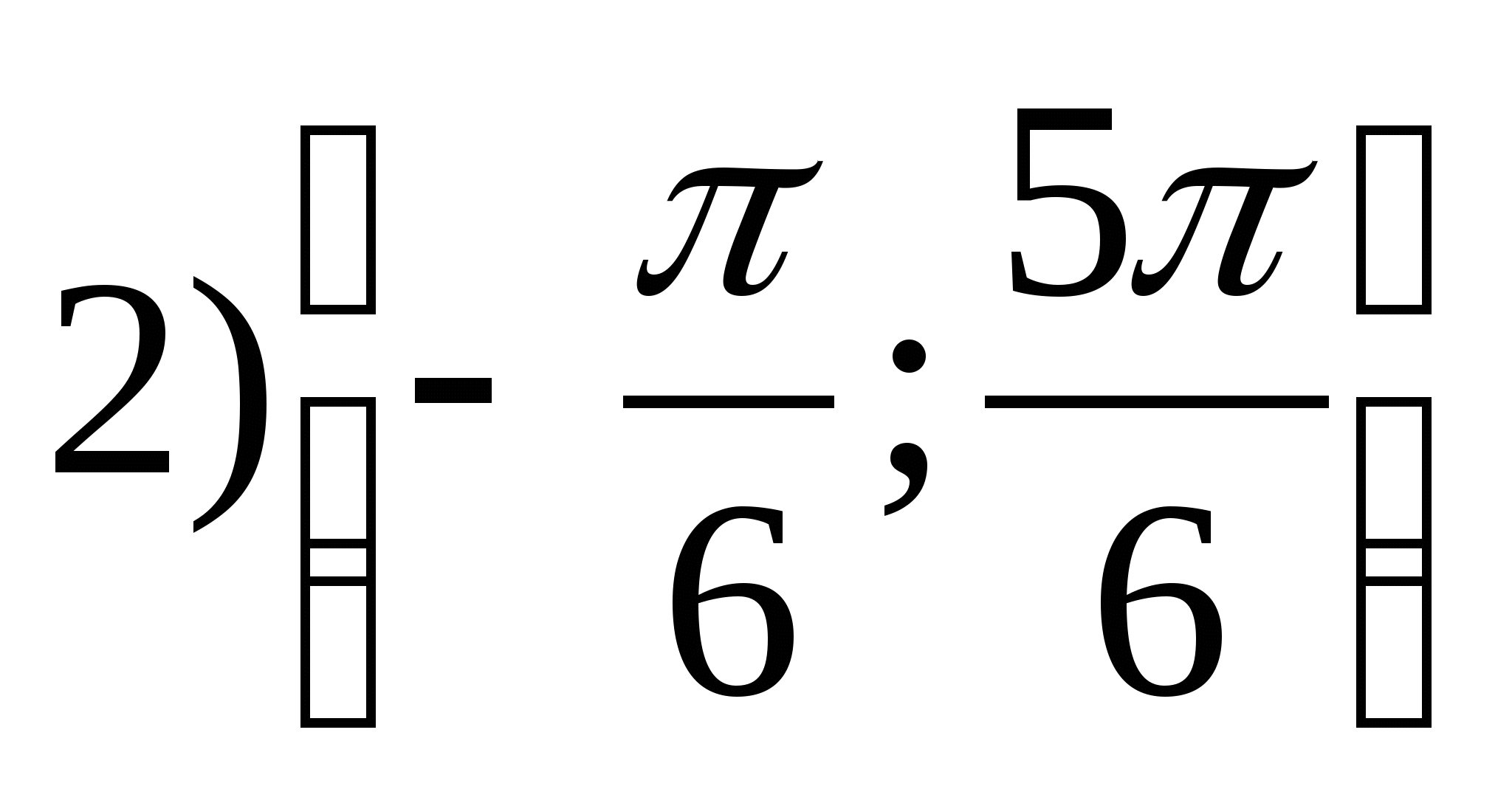
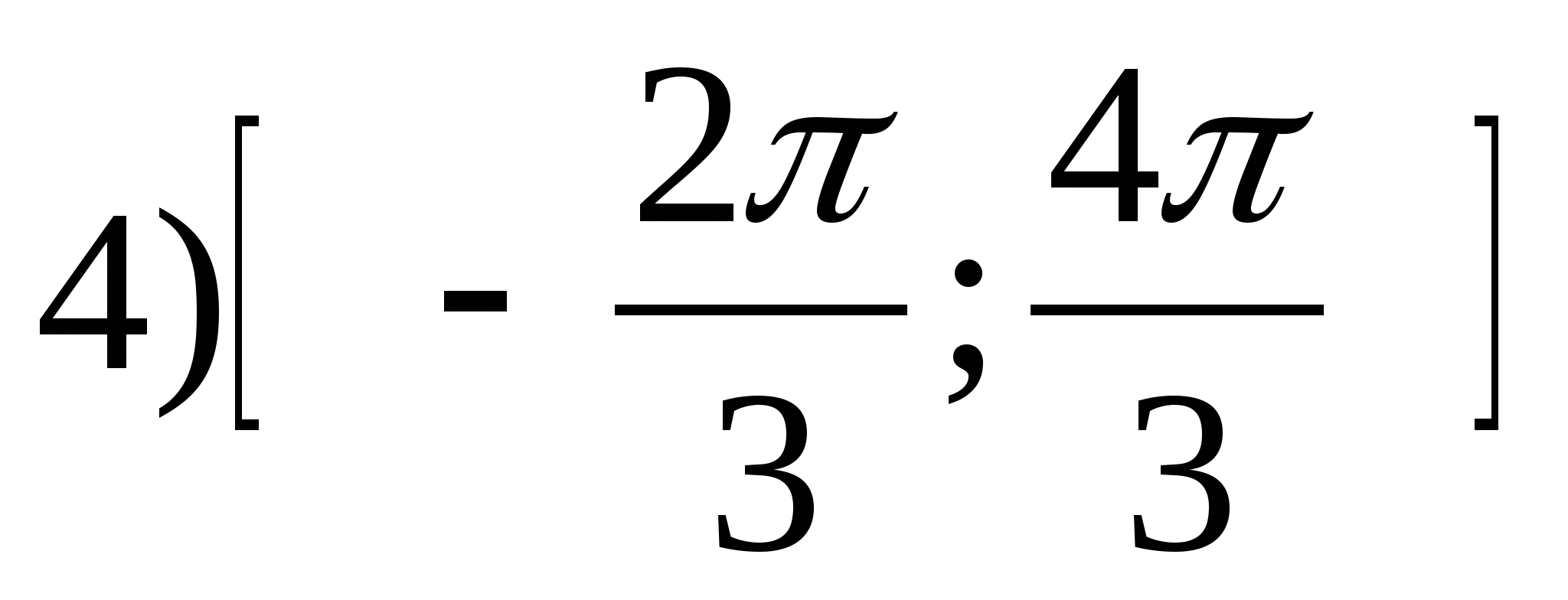
2. Znajdź największą całkowitą wartość funkcji

1) 4 2) 5 3) 6 4) 7

3. Która z poniższych liczb może być wartością funkcji

1) 0 2) 3 3) 6 4) 9

k równanie - k + grzech(2 x-1) = 2 rozwiązywalne?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Znajdź zestaw wartości funkcji według \u003d -sałata 2 3 x + 4.

1) 2) 3) 4)

6. Podaj najmniejszą wartość funkcji
pomiędzy

2) -1 3) 0 4) 1

7. Znajdź, ile liczb całkowitych mieści się w przedziale funkcji y = 12sałata 3 x +5 grzech 3 x.

1) 13 2) 27 3) 26 4) 14

Opcja 10

1. Znajdź zakres funkcji

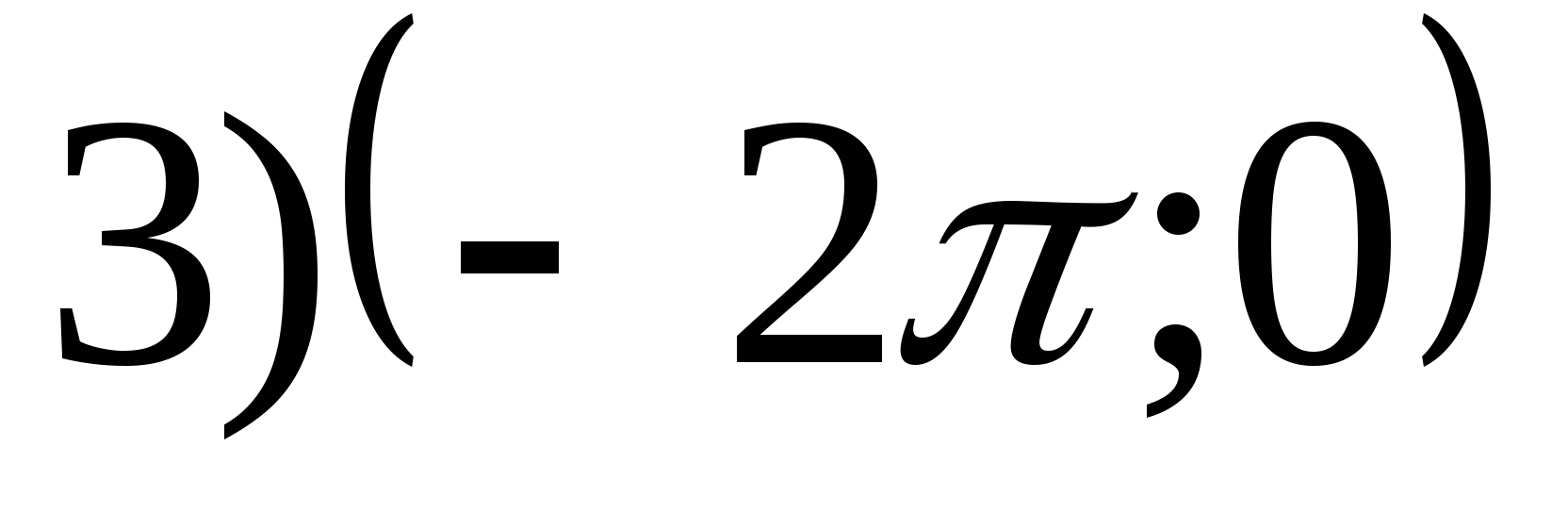
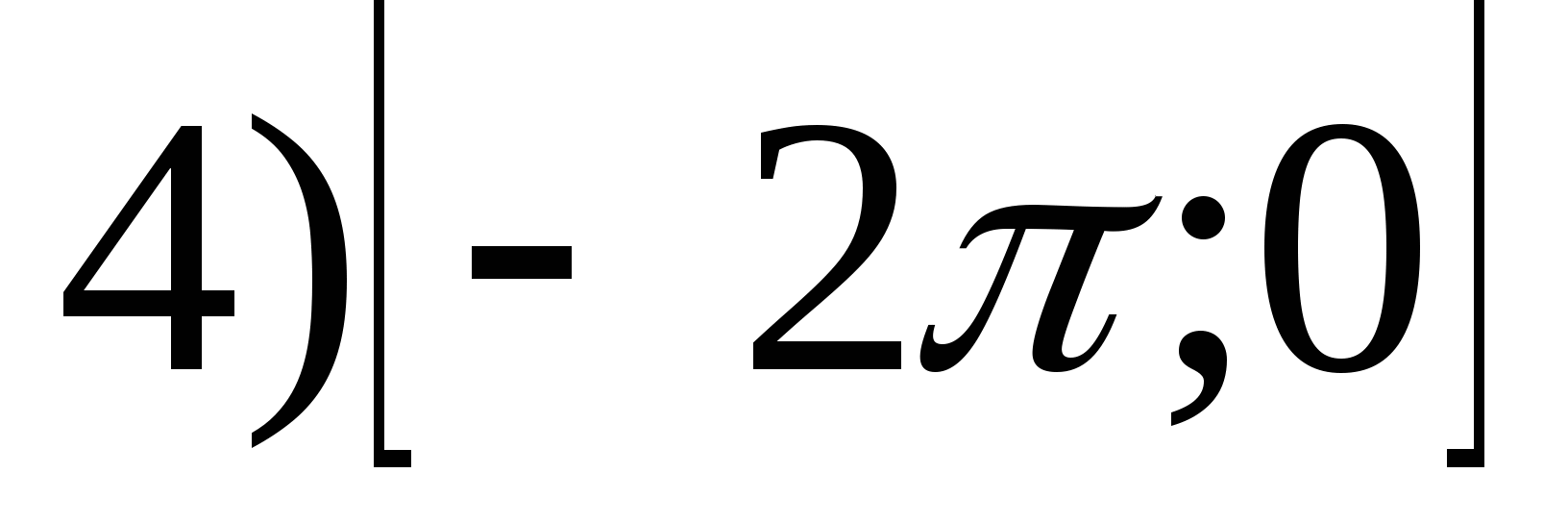
2. Znajdź najmniejszą wartość funkcji

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Która z poniższych liczb może być wartością funkcji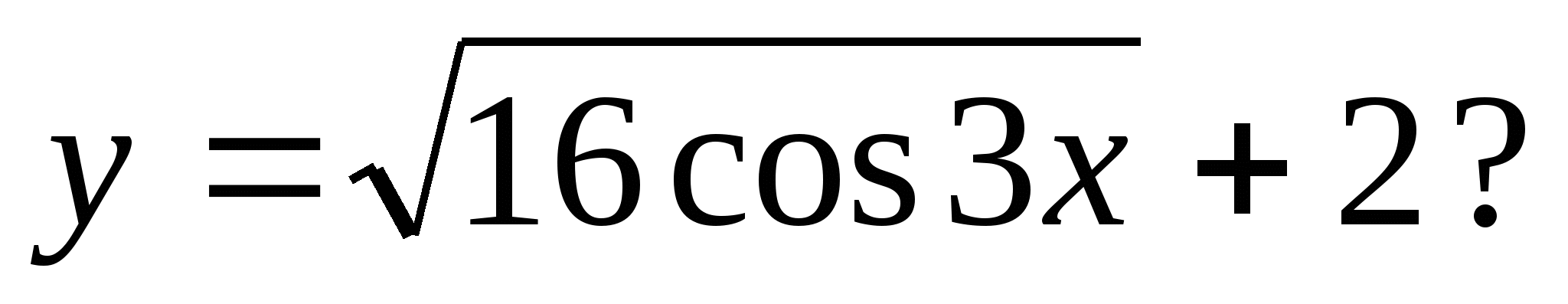

1) -4 2) -1 3) 3 4) 7

4. Przy jakich wartościach parametrum równanie sałata (3 x + 2)- m= 5 ma pierwiastki?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Znajdź zestaw wartości funkcji przez \u003d -2ktg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Podaj największą wartość funkcji
pomiędzy

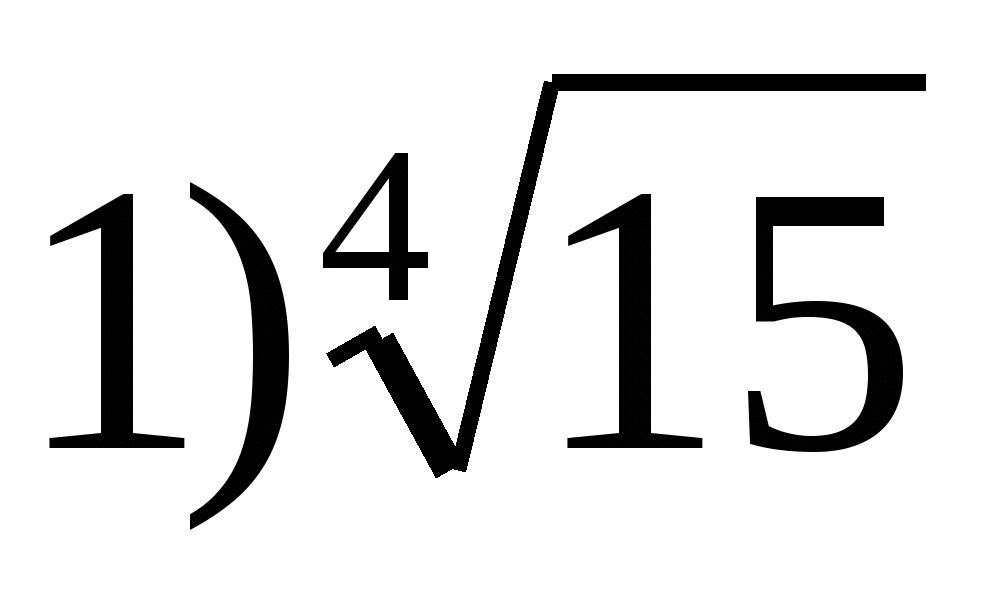2) 0 3) 2 4) 1

7. Znajdź, ile liczb całkowitych mieści się w przedziale funkcji

1) 30 2) 35 3) 17 4) 7

Zestaw wartości funkcji wykładniczych i logarytmicznych

opcja 1

1. Znajdź zakres funkcji

1) 4) (-∞;3)

2. Określ zestaw wartości funkcji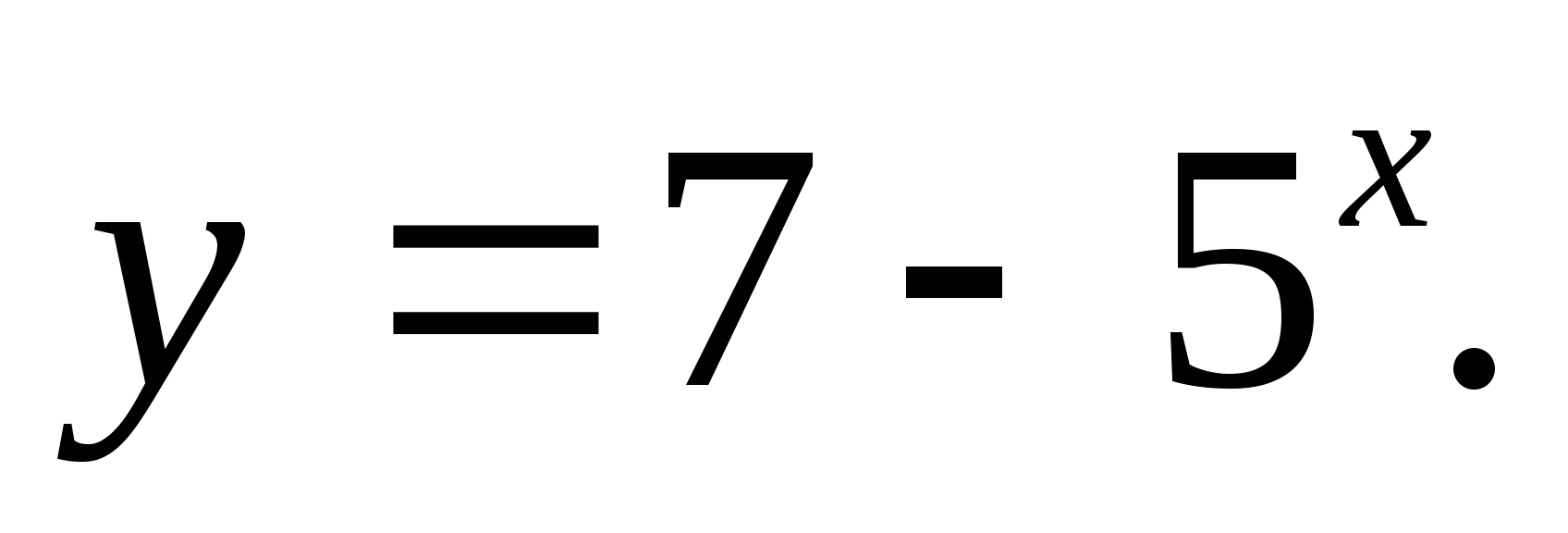

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Podaj najmniejszą całkowitą wartość funkcji

1) 1 2) -1 3) 0 4) -5

7. Podaj funkcję, której zbiorem wartości jest przedział (1;∞).

Opcja 2

1. Określ zestaw wartości funkcji

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Znajdź zakres funkcji

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Podaj najmniejszą liczbę całkowitą funkcji

1) -12 2) -11 3) -10 4) -15

4. Podaj liczbę, która nie należy do zbioru wartości funkcji

1) -42 2) 3 3) 1 4) -20

5. Określ zestaw wartości funkcji

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Podaj największą wartość całkowitą funkcji

1) 10 2) 3 3) 9 4) 2

7. Określ funkcję, której zbiorem wartości jest przedział

(-∞;13).

Opcja 5

1. Podaj najmniejszą całkowitą wartość funkcji

1) 0 2) -1 3) -2 4) -3

2. Która z poniższych liczb należy do zakresu funkcji

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Znajdź, w którym segmencie znajduje się funkcja
przyjmuje największą wartość 2 i najmniejszą wartość -3.

1) 2) (-5;2) 3) 4) (-3;2)

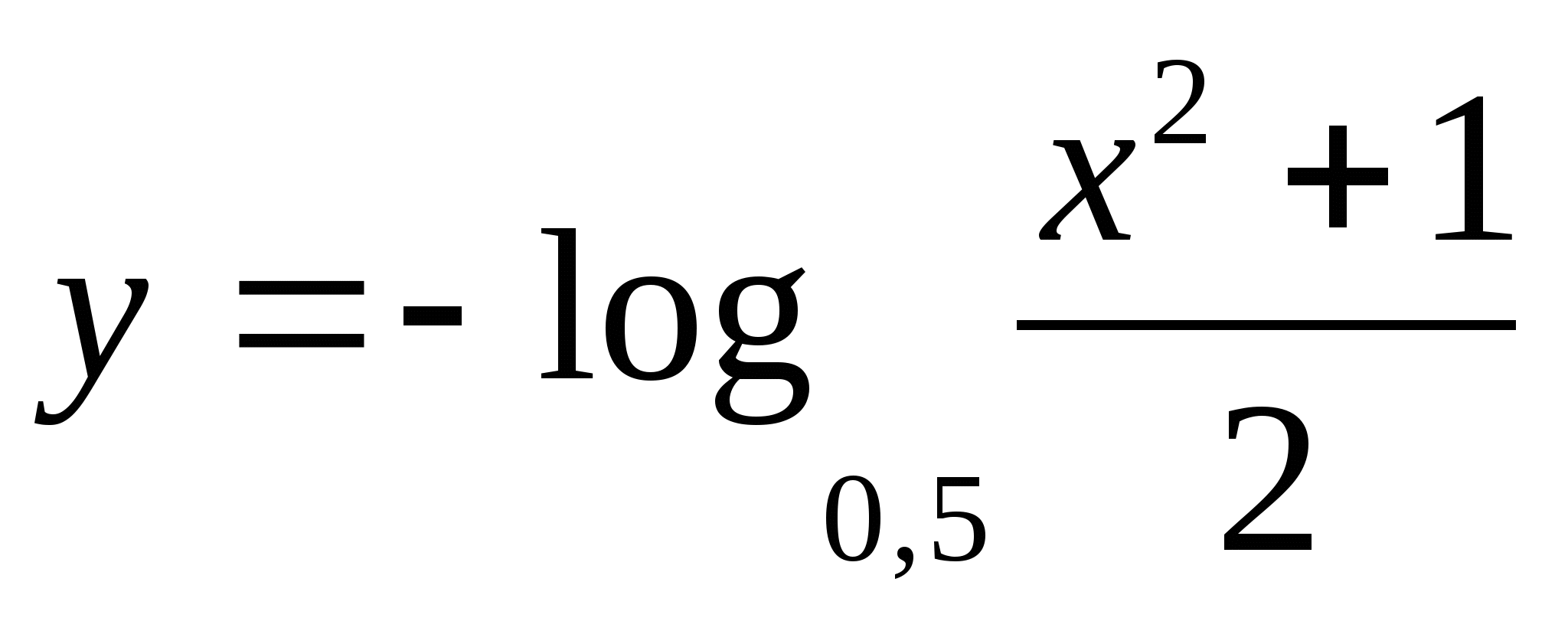pomiędzy

1) -1/2 2) 5 3) 2 4) 4

8. Znajdź sumę wszystkich liczb naturalnych nie zawartych w zbiorach wartości funkcji

1) 3 2) 6 3) 10 4) 8

Opcja 6

1. Podaj największą wartość całkowitą funkcji

1) 2 2) 4 3) 3 4) 5

2. Która z poniższych liczb nie należy do zakresu funkcji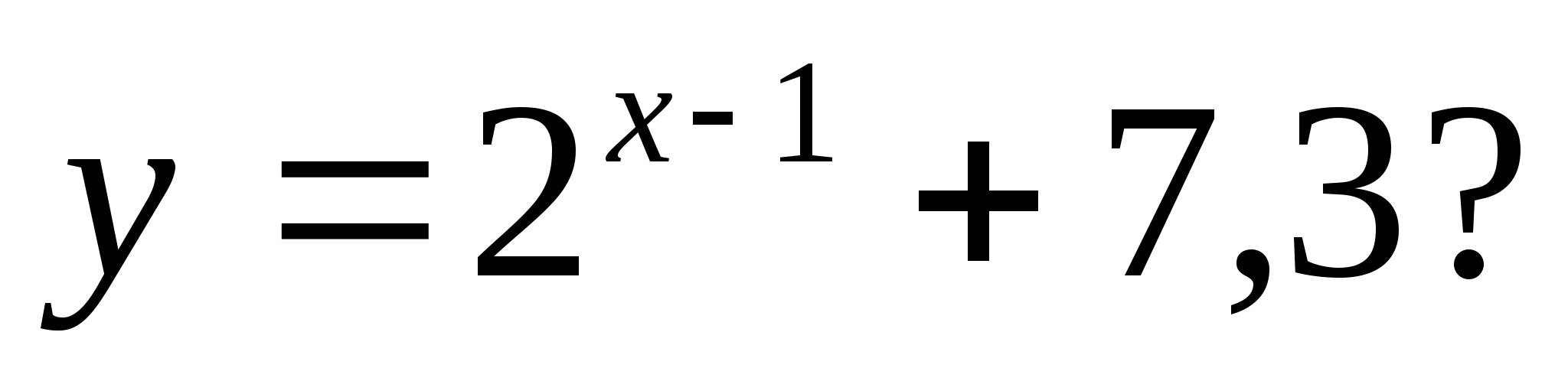

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Określ zestaw wartości funkcji

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Znajdź wszystkie punkty na OU, które są rzutami punktów wykresu funkcji

1) (0;∞) 2) 2) (-3;2) 3) [ dziennik 2 3;2] 4) (dziennik 2 3;2)

6. Znajdź, w którym segmencie znajduje się funkcja
przyjmuje najmniejszą wartość jako -2, a największą jako 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Podaj największą wartość funkcji
pomiędzy

[-0,9; 0]. 2. Znajdź najmniejszą wartość funkcji na odcinku.

4. Ile wartości całkowitych przyjmuje funkcja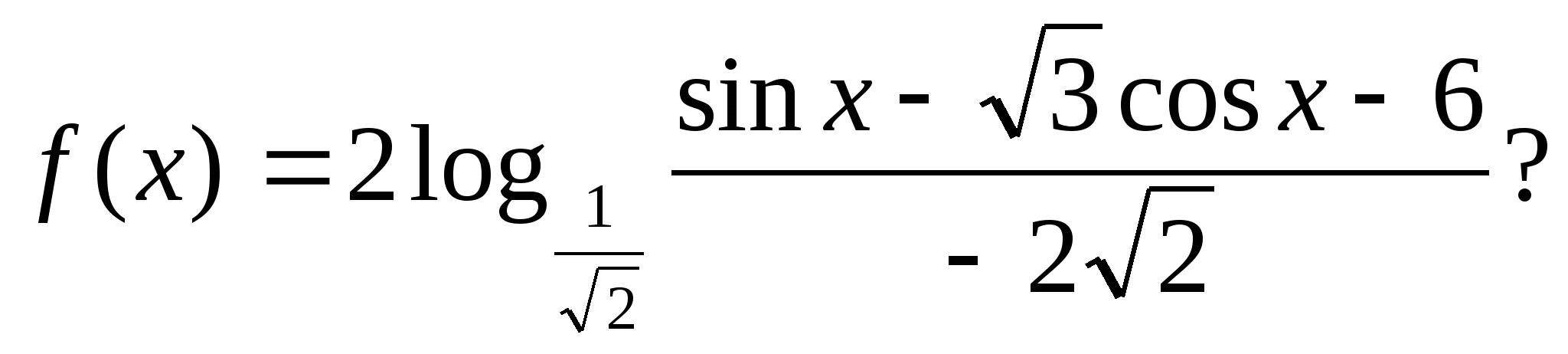

Odpowiedzi

Część 1

Zestaw wartości funkcji wykładniczej i logarytmicznej

Część 2

Pojęcie funkcji i wszystkiego, co się z nią wiąże, jest tradycyjnie złożone, nie do końca zrozumiałe. Szczególną przeszkodą w badaniu funkcji i przygotowaniu do egzaminu jest dziedzina definicji i zakres wartości (zmian) funkcji.
Często uczniowie nie widzą różnicy między dziedziną funkcji a dziedziną jej wartości.
A jeśli uczniom uda się opanować zadanie znalezienia dziedziny definicji funkcji, to zadanie znalezienia zestawu wartości funkcji sprawia im znaczne trudności.
Cel artykułu: zapoznanie się z metodami znajdowania wartości funkcji.
W wyniku rozważenia tego tematu zbadano materiał teoretyczny, rozważono metody rozwiązywania problemów znajdowania zestawów wartości funkcji, wybrano materiał dydaktyczny do samodzielnej pracy studentów.
Artykuł może być wykorzystany przez nauczyciela w przygotowaniu uczniów do egzaminów końcowych i wstępnych, podczas studiowania tematu „Zakres funkcji” na zajęciach fakultatywnych na przedmiotach fakultatywnych z matematyki.

I. Określenie zakresu funkcji.

Obszar (zbiór) wartości E(y) funkcji y = f(x) jest zbiorem takich liczb y 0 , dla każdej z nich istnieje taka liczba x 0, że: f(x 0) = y 0 .

Przypomnijmy sobie zakresy głównych funkcji elementarnych.

Rozważ stół.

Funkcjonować	Wiele wartości
y = k x + b	E(y) = (-∞;+∞)
y=x2n	E(y) =
y = cos x	E(y) = [-1;1]
y = tg x	E(y) = (-∞;+∞)
y = ctg x	E(y) = (-∞;+∞)
y = arcsin x	E(y) = [-π/2; π/2]
y = arcos x	E(y) =
y = arctg x	E(y) = (-π/2 ; π/2)
y = arcctg x	E(y) = (0; π)

Zauważ też, że zakresem dowolnego wielomianu parzystego stopnia jest przedział , gdzie n jest największą wartością tego wielomianu.

II. Właściwości funkcji używane do znajdowania zakresu funkcji

Aby skutecznie znaleźć zbiór wartości funkcji, trzeba dobrze znać własności podstawowych funkcji elementarnych, zwłaszcza ich dziedziny definicji, zakresy wartości oraz naturę monotoniczności. Przedstawmy własności ciągłych, monotonicznie różniczkowalnych funkcji, które są najczęściej wykorzystywane do znajdowania zbioru wartości funkcji.

Własności 2 i 3 są zwykle używane razem z właściwością funkcji elementarnej, aby była ciągła w swojej dziedzinie. W takim przypadku najprostsze i najkrótsze rozwiązanie problemu znalezienia zbioru wartości funkcji uzyskuje się na podstawie właściwości 1, jeśli możliwe jest określenie monotoniczności funkcji za pomocą prostych metod. Rozwiązanie problemu jest jeszcze bardziej uproszczone, jeśli dodatkowo funkcja jest parzysta lub nieparzysta, okresowa itp. Dlatego przy rozwiązywaniu problemów znajdowania zbiorów wartości funkcji należy sprawdzić iw razie potrzeby wykorzystać następujące właściwości funkcji:

• ciągłość;
• monotonia;
• różniczkowalność;
• parzyste, nieparzyste, okresowe itp.

Proste zadania polegające na znalezieniu zestawu wartości funkcji są w większości zorientowane:

a) zastosowanie najprostszych oszacowań i ograniczeń: (2 x > 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x ? 1 itd.);

b) aby wybrać pełny kwadrat: x 2 - 4x + 7 \u003d (x - 2) 2 + 3;

c) dla przekształcenia wyrażeń trygonometrycznych: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

d) korzystając z monotoniczności funkcji x 1/3 + 2 x-1 wzrasta o R.

III. Rozważ sposoby znajdowania zakresów funkcji.

a) sekwencyjne znajdowanie wartości argumentów funkcji zespolonych;
b) metoda oceny;
c) wykorzystanie własności ciągłości i monotoniczności funkcji;
d) wykorzystanie instrumentu pochodnego;
e) użycie największej i najmniejszej wartości funkcji;
f) metoda graficzna;
g) sposób wprowadzania parametrów;
h) metoda funkcji odwrotnych.

Istotę tych metod ujawnimy na konkretnych przykładach.

Przykład 1: Znajdź zakres E(y) funkcje y = log 0,5 (4 - 2 3 x - 9 x).

Rozwiążmy ten przykład, znajdując kolejno wartości złożonych argumentów funkcji. Po wybraniu pełnego kwadratu pod logarytmem przekształcamy funkcję

y = log 0,5 (5 - (1 + 2 3 x - 3 2x)) = log 0,5 (5 - (3 x + 1) 2)

I kolejno znajdź zestawy wartości jego złożonych argumentów:

E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)

Oznaczać t= 5 – (3 x +1) 2 , gdzie -∞≤ t≤4. Zatem problem sprowadza się do znalezienia zbioru wartości funkcji y = log 0,5 t na promieniu (-∞;4) . Ponieważ funkcja y = log 0,5 t jest zdefiniowana tylko w, to jej zbiór wartości na promieniu (-∞;4) pokrywa się ze zbiorem wartości funkcji na przedziale (0;4), który jest przecięciem promienia (-∞;4) z dziedziną definicji (0;+∞) funkcji logarytmicznej. Na przedziale (0;4) funkcja ta jest ciągła i malejąca. Na t> 0, dąży do +∞, a kiedy t = 4 przyjmuje wartość -2, więc E(y) =(-2, +∞).

Przykład 2: Znajdź zakres funkcji

y = cos7x + 5cosx

Rozwiążmy ten przykład metodą oszacowań, której istotą jest oszacowanie funkcji ciągłej z dołu i z góry oraz wykazanie, że funkcja osiąga dolną i górną granicę oszacowań. W tym przypadku zbieżność zbioru wartości funkcji z przedziałem od dolnej granicy oszacowania do górnej jest określona przez ciągłość funkcji i brak dla niej innych wartości.

Z nierówności -1≤cos7x?1, -5≤5cosx?5 otrzymujemy oszacowanie -6≤y?6. Dla x = p i x = 0 funkcja przyjmuje wartości -6 i 6, tj. osiąga dolną i górną granicę. Jako liniowa kombinacja funkcji ciągłych cos7x i cosx, funkcja y jest ciągła wzdłuż całej osi liczbowej, dlatego dzięki właściwości funkcji ciągłej przyjmuje wszystkie wartości od -6 do 6 włącznie i tylko one, ponieważ , ze względu na nierówności -6≤y?6, inne wartości są niemożliwe. W konsekwencji, E(y)= [-6;6].

Przykład 3: Znajdź zakres mi(f) Funkcje f(x)= cos2x + 2cosx.

Korzystając ze wzoru na cosinus podwójnego kąta, przekształcamy funkcję f(x)= 2cos 2 x + 2cosx – 1 i oznaczmy t= cosx. Następnie f(x)= 2t 2 + 2t – 1. Ponieważ E(cosx) =

[-1;1], następnie zakres funkcji f(x) pokrywa się ze zbiorem wartości funkcji g (t)\u003d 2t 2 + 2t - 1 na odcinku [-1; 1], który znajdziemy metodą graficzną. Po wykreśleniu funkcji y = 2t 2 + 2t - 1 = 2(t + 0,5) 2 - 1,5 na przedziale [-1; 1] znajdujemy mi(f) = [-1,5; 3].

Uwaga – Wiele problemów z parametrem sprowadza się do znalezienia zbioru wartości funkcji, głównie związanych z rozwiązywalnością i liczbą rozwiązań równania i nierówności. Na przykład równanie f(x)= a jest rozwiązywalne wtedy i tylko wtedy, gdy

aE(f) Podobnie równanie f(x)= a ma co najmniej jeden pierwiastek znajdujący się na pewnym przedziale X lub nie ma pierwiastka na tym przedziale wtedy i tylko wtedy, gdy a należy lub nie należy do zbioru wartości funkcji f(x) na przedziale X. Badamy również za pomocą zbioru wartości funkcji i nierówności f(x)≠ a, f(x)> itp. W szczególności, f(x)≠ i dla wszystkich dopuszczalnych wartości x, jeśli a E(f)

Przykład 4. Dla jakich wartości parametru a równanie (x + 5) 1/2 = a (x 2 + 4) ma pojedynczy pierwiastek na odcinku [-4;-1].

Zapiszmy równanie w postaci (x + 5) 1/2 / (x 2 + 4) = a. Ostatnie równanie ma co najmniej jeden pierwiastek na odcinku [-4;-1] wtedy i tylko wtedy, gdy a należy do zbioru wartości funkcji f(x) =(x + 5) 1/2 / (x 2 + 4) na odcinku [-4;-1]. Znajdźmy ten zbiór korzystając z własności ciągłości i monotoniczności funkcji.

Na odcinku [-4;-1] funkcja y = xІ + 4 jest ciągła, malejąca i dodatnia, stąd funkcja g(x) = 1/(x 2 + 4) jest ciągły i rośnie w tym przedziale, ponieważ przy dzieleniu przez funkcję dodatnią charakter monotoniczności funkcji zmienia się na przeciwny. Funkcjonować h(x) =(x + 5) 1/2 jest ciągła i rosnąca w swojej dziedzinie D(h) =[-5;+∞), aw szczególności na przedziale [-4;-1], gdzie również jest dodatnia. Następnie funkcja f(x)=g(x) h(x), jako iloczyn dwóch funkcji ciągłych, rosnącej i dodatniej, jest też ciągła i rośnie na odcinku [-4;-1], więc jej zbiór wartości na [-4;-1] to odcinek [ f(-4); f(-1)] = . Zatem równanie ma rozwiązanie w przedziale [-4;-1] i jedyne (według własności ciągłej funkcji monotonicznej) dla 0,05 ≤ a ≤ 0,4

Komentarz. Rozwiązywalność równania f(x) = za na pewnym przedziale X jest równoważne przynależności wartości parametru a zbiór wartości funkcji f(x) na X. Dlatego zestaw wartości funkcji f(x) na przedziale X pokrywa się ze zbiorem wartości parametrów a, dla którego równanie f(x) = za ma co najmniej jeden pierwiastek z przedziału X. W szczególności zakres wartości mi(f) Funkcje f(x) pasuje do zestawu wartości parametrów a, dla którego równanie f(x) = za ma co najmniej jeden pierwiastek.

Przykład 5: Znajdź zakres mi(f) Funkcje

Rozwiążmy przykład, wprowadzając parametr, zgodnie z którym mi(f) pasuje do zestawu wartości parametrów a, dla którego równanie

ma co najmniej jeden pierwiastek.

Gdy a=2, równanie jest liniowe - 4x - 5 = 0 z niezerowym współczynnikiem dla nieznanego x, więc ma rozwiązanie. Dla a≠2 równanie jest kwadratowe, więc jest rozwiązywalne wtedy i tylko wtedy, gdy jego dyskryminator

Ponieważ punkt a = 2 należy do odcinka

następnie żądany zestaw wartości parametrów a, stąd zakres wartości mi(f) będzie cały segment.

Jako bezpośrednie rozwinięcie metody wprowadzania parametru przy znajdowaniu zestawu wartości funkcji możemy rozważyć metodę funkcji odwrotnej, aby znaleźć, którą należy rozwiązać równanie dla x f(x)=y, biorąc pod uwagę y jako parametr. Jeśli to równanie ma unikalne rozwiązanie x=g(y), a następnie zakres mi(f) oryginalna funkcja f(x) pokrywa się z dziedziną definicji D(g) funkcja odwrotna g(y). Jeśli równanie f(x)=y ma wiele rozwiązań x = g 1 (y), x \u003d g 2 (y) itd., w takim razie mi(f) jest równa sumie zakresów definicji funkcji g 1 (y), g 2 (y) itp.

Przykład 6: Znajdź zakres E(y) funkcje y = 5 2/(1-3x).

Z równania

znajdź funkcję odwrotną x = log 3 ((log 5 y – 2)/(log 5 y)) i jej dziedzinę D(x):

Ponieważ równanie dla x ma unikalne rozwiązanie, to

E(y) = D(x) = (0; 1)(25;+∞ ).

Jeśli dziedzina funkcji składa się z kilku przedziałów lub funkcja w różnych przedziałach jest określona różnymi wzorami, to aby znaleźć dziedzinę funkcji, należy znaleźć zestawy wartości funkcji w każdym przedziale i wziąć ich unia.

Przykład 7: Znajdź zakresy f(x) oraz f(f(x)), gdzie

f(x) na promieniu (-∞;1], gdzie pokrywa się z wyrażeniem 4 x + 9 4 -x + 3. Oznacz t = 4 x. Następnie f(x) = t + 9/t + 3, gdzie 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x) na promieniu (-∞;1] pokrywa się ze zbiorem wartości funkcji g(t) = t + 9/t + 3, na przedziale (0;4], który znajdujemy za pomocą pochodnej g'(t) \u003d 1 - 9 / t 2. Na przedziale (0;4] pochodna g'(t) jest zdefiniowany i znika w tym miejscu t=3. o 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g(t) maleje, aw przedziale (3;4) rośnie, pozostając ciągłą na całym przedziale (0;4), więc g (3)= 9 - najmniejsza wartość tej funkcji na przedziale (0; 4], podczas gdy jej największa wartość nie istnieje, więc gdy t→0 właściwa funkcja g(t)→+∞. Następnie, według właściwości funkcji ciągłej, zestaw wartości funkcji g(t) na przedziale (0;4], a więc zbiór wartości f(x) na (-∞;-1], pojawi się promień .

Teraz, łącząc przedziały - zestawy wartości funkcji f(f(x)), oznacz t = fa(x). Następnie f(f(x)) = f(t), gdzie t funkcjonować f(t)= 2kos( x-1) 1/2+7 i znowu przyjmuje wszystkie wartości od 5 do 9 włącznie, tj. zasięg mi(fІ) = mi(f(f(x))) =.

Podobnie oznaczający z = f(f(x)), możesz znaleźć zakres E(f3) Funkcje f(f(f(x))) = f(z), gdzie 5 ≤ z ≤ 9 itd. Upewnić się, że mi(f 3) = .

Najbardziej uniwersalną metodą znajdowania zbioru wartości funkcji jest posługiwanie się największą i najmniejszą wartością funkcji w danym przedziale.

Przykład 8. Dla jakich wartości parametru R nierówność 8 x - p ≠ 2x+1 – 2x zachodzi dla wszystkich -1 ≤ x< 2.

Oznaczanie t = 2 x, zapisujemy nierówność jako p ≠ t 3 - 2 t 2 + t. Dlatego t = 2 x jest stale rosnącą funkcją na R, wtedy dla -1 ≤ x< 2 переменная

2 -1 ≤t<2 2 ↔

0,5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда R różne od wartości funkcji f(t) \u003d t 3 - 2t 2 + t przy 0,5 ≤t< 4.

Najpierw znajdźmy zbiór wartości funkcji f(t) na przedziale, w którym wszędzie ma pochodną f'(t) = 3t 2 - 4t + 1. W konsekwencji, f(t) jest różniczkowalna, a zatem ciągła na odcinku . Z równania f'(t) = 0 znaleźć punkty krytyczne funkcji t=1/3, t=1, z których pierwszy nie należy do segmentu , a drugi do niego należy. Dlatego f(0,5) = 1/8, f(1) = 0, f(4) = 36, wtedy, zgodnie z właściwością funkcji różniczkowalnej, 0 jest najmniejszą, a 36 jest największą wartością funkcji f(t) na segmencie. Następnie f(t), jako funkcja ciągła, przyjmuje na odcinku wszystkie wartości od 0 do 36 włącznie, a wartość 36 przyjmuje tylko wtedy, gdy t=4, więc dla 0,5 ≤ t< 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Weźmy problem, w którym konieczne jest określenie zakresu wartości arcus sinus.

Przykład 1

Stan: znajdź zakres y = a r c sin x .

Rozwiązanie

W ogólnym przypadku dziedzina definicji arcus sinus znajduje się na przedziale [ - 1 ; jeden ] . Musimy wyznaczyć na nim największą i najmniejszą wartość podanej funkcji.

y "= a r c grzech x" = 1 1 - x 2

Wiemy, że pochodna funkcji będzie dodatnia dla wszystkich wartości x znajdujących się w przedziale [-1; 1 ] , to znaczy w całej dziedzinie definicji funkcja arcus sinus będzie rosła. Oznacza to, że przyjmie najmniejszą wartość, gdy x jest równe - 1, a największą - gdy x jest równe 1.

m ja n x ∈ - 1; 1 za r do grzech x = za r do grzech - 1 = - π 2 m za x x ∈ - 1 ; 1 za r do grzech x = za r do grzech 1 = π 2

Zatem zakres funkcji arcus sinus będzie równy E (ar c sin x) = - π 2 ; π 2 .

Odpowiadać: mi (ar c sin x) \u003d - π 2; π 2

Przykład 2

Stan: oblicz zakres y = x 4 - 5 x 3 + 6 x 2 na danym odcinku [ 1 ; cztery ] .

Rozwiązanie

Wszystko, co musimy zrobić, to obliczyć największą i najmniejszą wartość funkcji w zadanym przedziale.

Aby wyznaczyć punkty ekstremalne, należy wykonać następujące obliczenia:

y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1;4 i l oraz 4 x 2 - 15 x + 12 = 0 re = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1 ;4 ;x3 = 15 + 338 ≈ 2,59 ∈ 1;4

Teraz znajdźmy wartości danej funkcji na końcach odcinka i punktach x 2 = 15 - 33 8 ; x 3 \u003d 15 + 33 8:

y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2. 08 y 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 r (4) = 4 4 - 5 4 3 + 6 4 2 = 32

Oznacza to, że zbiór wartości funkcji będzie określony przez segment 117 - 165 33 512 ; 32 .

Odpowiadać: 117 - 165 33 512 ; 32 .

Przejdźmy do znalezienia zbioru wartości funkcji ciągłej y = f (x) w przedziałach (a ; b) , oraz a ; + ∞ , - ∞ ; b , -∞ ; +∞ .

Zacznijmy od wyznaczenia największego i najmniejszego punktu oraz przedziałów wzrostu i spadku w danym przedziale. Następnie będziemy musieli obliczyć granice jednostronne na końcach przedziału i/lub granice w nieskończoności. Innymi słowy, musimy określić zachowanie funkcji w danych warunkach. Do tego mamy wszystkie niezbędne dane.

Przykład 3

Stan: oblicz zakres funkcji y = 1 x 2 - 4 na przedziale (- 2 ; 2) .

Rozwiązanie

Wyznacz największą i najmniejszą wartość funkcji w zadanym przedziale

y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2)

Otrzymaliśmy maksymalną wartość równą 0 , ponieważ w tym momencie zmienia się znak funkcji i wykres zaczyna się zmniejszać. Zobacz ilustrację:

Oznacza to, że y (0) = 1 0 2 - 4 = - 1 4 będzie maksymalną wartością funkcji.

Teraz zdefiniujmy zachowanie funkcji dla x, które dąży do -2 po prawej stronie i +2 po lewej stronie. Innymi słowy, znajdujemy jednostronne granice:

limit x → - 2 + 0 1 x 2 - 4 = limit x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ granica x → 2 + 0 1 x 2 - 4 = granica x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞

Otrzymaliśmy, że wartości funkcji wzrosną od minus nieskończoności do - 1 4, gdy argument zmieni się z - 2 na 0 . A gdy argument zmieni się z 0 na 2, wartości funkcji maleją w kierunku minus nieskończoności. Dlatego zestaw wartości danej funkcji na potrzebnym nam przedziale będzie (- ∞ ; - 1 4 ] .

Odpowiadać: (- ∞ ; - 1 4 ] .

Przykład 4

Stan: wskaż zbiór wartości y = t g x w podanym przedziale - π 2 ; π 2 .

Rozwiązanie

Wiemy, że na ogół pochodna tangensa w - π 2; π 2 będzie dodatnie, to znaczy funkcja będzie rosła. Teraz zdefiniujmy, jak funkcja zachowuje się w danych granicach:

lim x → π 2 + 0 t sol x = t sol - π 2 + 0 = - ∞ lim x → π 2 - 0 t sol x = t sol π 2 - 0 = + ∞

Uzyskaliśmy wzrost wartości funkcji od minus nieskończoności do plus nieskończoności, gdy argument zmienia się z - π 2 na π 2 i możemy powiedzieć, że zbiór rozwiązań tej funkcji będzie zbiorem wszystkich rzeczywistych liczby.

Odpowiadać: - ∞ ; + ∞ .

Przykład 5

Stan: wyznacz zakres funkcji logarytmu naturalnego y = ln x .

Rozwiązanie

Wiemy, że ta funkcja jest zdefiniowana dla dodatnich wartości argumentu D(y) = 0; +∞ . Pochodna na podanym przedziale będzie dodatnia: y " = ln x " = 1 x . Oznacza to, że funkcja jest na nim rosnąca. Następnie musimy zdefiniować jednostronną granicę dla przypadku, gdy argument dąży do 0 (po prawej stronie) i gdy x dąży do nieskończoności:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Odkryliśmy, że wartości funkcji wzrosną od minus nieskończoności do plus nieskończoności, gdy wartości x zmienią się od zera do plus nieskończoności. Oznacza to, że zbiór wszystkich liczb rzeczywistych jest zakresem funkcji logarytmu naturalnego.

Odpowiadać: zbiór wszystkich liczb rzeczywistych to zakres funkcji logarytmu naturalnego.

Przykład 6

Stan: wyznacz zakres funkcji y = 9 x 2 + 1 .

Rozwiązanie

Ta funkcja jest zdefiniowana pod warunkiem, że x jest liczbą rzeczywistą. Obliczmy największą i najmniejszą wartość funkcji, a także przedziały jej wzrostu i spadku:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

W rezultacie ustaliliśmy, że funkcja ta będzie maleć, jeśli x ≥ 0; zwiększać, jeśli x ≤ 0; ma punkt maksymalny y (0) = 9 0 2 + 1 = 9, gdy zmienna wynosi 0 .

Zobaczmy, jak funkcja zachowuje się w nieskończoności:

granica x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 granica x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0

Z zapisu widać, że wartości funkcji w tym przypadku będą dążyć asymptotycznie do 0.

Podsumowując: gdy argument zmienia się od minus nieskończoności do zera, to wartości funkcji rosną od 0 do 9. Gdy wartości argumentów przejdą od 0 do plus nieskończoności, odpowiednie wartości funkcji zmniejszą się z 9 do 0 . Przedstawiliśmy to na rysunku:

Pokazuje, że zakresem funkcji będzie przedział E (y) = (0 ; 9 ]

Odpowiadać: mi (y) = (0 ; 9 ]

Jeśli musimy wyznaczyć zbiór wartości funkcji y = f (x) na przedziałach [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , to będziemy musieli przeprowadzić dokładnie te same badania. Nie będziemy jeszcze analizować tych przypadków: spotkamy się z nimi później w problemach .

Ale co, jeśli dziedziną pewnej funkcji jest suma kilku przedziałów? Następnie musimy obliczyć zestawy wartości na każdym z tych przedziałów i połączyć je.

Przykład 7

Stan: określ, jaki będzie zakres y = x x - 2 .

Rozwiązanie

Ponieważ mianownika funkcji nie należy zamieniać na 0 , to D (y) = - ∞ ; 2 ∪ 2 ; +∞ .

Zacznijmy od zdefiniowania zbioru wartości funkcji na pierwszym segmencie - ∞ ; 2, który jest otwartą belką. Wiemy, że funkcja na nim będzie maleć, czyli pochodna tej funkcji będzie ujemna.

granica x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ granica x → - ∞ x x - 2 = granica x → - ∞ x - 2 + 2 x - 2 = granica x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Następnie w przypadkach, gdy argument zmienia się w kierunku minus nieskończoności, wartości funkcji asymptotycznie zbliżają się do 1 . Jeśli wartości x zmienią się z minus nieskończoności na 2, to wartości zmniejszą się od 1 do minus nieskończoności, tj. funkcja na tym segmencie przyjmie wartości z przedziału - ∞ ; jeden . Wykluczamy jedność z naszego rozumowania, ponieważ wartości funkcji do niej nie docierają, a jedynie asymptotycznie się do niej zbliżają.

Dla belki otwartej 2 ; + ∞ wykonujemy dokładnie te same czynności. Funkcja na nim jest również malejąca:

granica x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ granica x → + ∞ x x - 2 = granica x → + ∞ x - 2 + 2 x - 2 = granica x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

Wartości funkcji na tym segmencie są określone przez zbiór 1; +∞ . Oznacza to, że zakres wartości funkcji określony w warunku, którego potrzebujemy, będzie sumą zbiorów - ∞; 1 i 1; +∞ .

Odpowiadać: mi (y) = - ∞ ; 1 ∪ 1 ; +∞ .

Widać to na wykresie:

Szczególnym przypadkiem są funkcje okresowe. Ich obszar wartości pokrywa się ze zbiorem wartości na przedziale odpowiadającym okresowi tej funkcji.

Przykład 8

Stan: określ zakres sinus y = sin x .

Rozwiązanie

Sinus odnosi się do funkcji okresowej, a jej okres wynosi 2 pi. Bierzemy segment 0; 2 π i zobacz jaki będzie na nim zbiór wartości.

y " = (grzech x) " = sałata x y " = 0 ⇔ sałata x = 0 ⇔ x = π 2 + πk , k ∈ Z

w ciągu 0; 2 π funkcja będzie miała punkty skrajne π 2 i x = 3 π 2 . Obliczmy, jakie wartości funkcji będą w nich równe, a także na granicach odcinka, po czym wybieramy największą i najmniejszą wartość.

y (0) = grzech 0 = 0 y π 2 = grzech π 2 = 1 y 3 π 2 = grzech 3 π 2 = - 1 y (2 π) = grzech (2 π) = 0 ⇔ min x ∈ 0 ; 2 π grzech x = grzech 3 π 2 = - 1 , max x ∈ 0 ; 2 π sinx \u003d grzech π 2 \u003d 1

Odpowiadać: mi (sinx) = - 1 ; jeden .

Jeśli chcesz poznać zakresy funkcji, takich jak wykładniczy, wykładniczy, logarytmiczny, trygonometryczny, odwrotny trygonometryczny, radzimy ponownie przeczytać artykuł o podstawowych funkcjach elementarnych. Teoria, którą tutaj prezentujemy, pozwala nam przetestować podane tam wartości. Pożądane jest ich poznanie, ponieważ często są one wymagane przy rozwiązywaniu problemów. Jeśli znasz zakresy funkcji głównych, możesz łatwo znaleźć zakresy funkcji, które są uzyskiwane z elementarnych za pomocą transformacji geometrycznej.

Przykład 9

Stan: wyznacz przedział y = 3 a r do cos x 3 + 5 π 7 - 4 .

Rozwiązanie

Wiemy, że odcinek od 0 do pi jest zakresem odwrotnego cosinusa. Innymi słowy, E (a r c cos x) = 0; π lub 0 ≤ za r do sałata x ≤ π . Funkcję a r c cos x 3 + 5 π 7 możemy otrzymać z arc cosinus przesuwając i rozciągając ją wzdłuż osi O x, ale takie przekształcenia nic nam nie dadzą. Stąd 0 ≤ a r do cos x 3 + 5 π 7 ≤ π .

Funkcję 3 a r c cos x 3 + 5 π 7 można otrzymać z odwrotności cosinusa a r c cos x 3 + 5 π 7 przez rozciągnięcie wzdłuż osi y, tj. 0 ≤ 3 za r do sałata x 3 + 5 π 7 ≤ 3 π . Ostateczna transformacja to przesunięcie wzdłuż osi O y o 4 wartości. W rezultacie otrzymujemy podwójną nierówność:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4

Otrzymaliśmy, że potrzebny nam zakres będzie równy E (y) = - 4 ; 3 pi - 4 .

Odpowiadać: mi (y) = - 4; 3 pi - 4 .

Napiszmy jeszcze jeden przykład bez wyjaśnień, bo jest całkowicie podobny do poprzedniego.

Przykład 10

Stan: oblicz jaki będzie zakres funkcji y = 2 2 x - 1 + 3 .

Rozwiązanie

Przepiszmy funkcję podaną w warunku jako y = 2 · (2 ​​x - 1) - 1 2 + 3 . Dla funkcji potęgowej y = x - 1 2 zakres będzie określony w przedziale 0 ; + ∞ , tj. x - 1 2 > 0 . W tym przypadku:

2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3

Więc E (y) = 3; +∞ .

Odpowiadać: mi (y) = 3; +∞ .

Przyjrzyjmy się teraz, jak znaleźć zakres funkcji, który nie jest ciągły. Aby to zrobić, musimy podzielić cały obszar na przedziały i znaleźć na każdym z nich zestawy wartości, a następnie połączyć to, co mamy. Aby lepiej to zrozumieć, radzimy zapoznać się z głównymi typami punktów przerwania funkcji.

Przykład 11

Stan: mając daną funkcję y = 2 grzech x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3 . Oblicz jego zasięg.

Rozwiązanie

Ta funkcja jest zdefiniowana dla wszystkich wartości x. Przeanalizujmy to pod kątem ciągłości z wartościami argumentu równymi - 3 i 3:

lim x → - 3 - 0 f (x) = lim x → - 3 2 grzech x 2 - 4 = 2 grzech - 3 2 - 4 = - 2 grzech 3 2 - 4 lim x → - 3 + 0 f (x) = granica x → - 3 (1) = - 1 ⇒ granica x → - 3 - 0 fa (x) ≠ granica x → - 3 + 0 fa (x)

Mamy nieodwracalną nieciągłość pierwszego rodzaju o wartości argumentu - 3 . Gdy się do tego zbliżysz, wartości funkcji będą dążyć do - 2 sin 3 2 - 4 , a ponieważ x dąży do - 3 po prawej stronie, wartości będą dążyć do - 1 .

lim x → 3 - 0 f(x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f(x) = lim x → 3 + 0 1 x - 3 = + ∞

W punkcie 3 mamy nieusuwalną nieciągłość drugiego rodzaju. Gdy funkcja dąży do niej, jej wartości zbliżają się do -1, natomiast dążąc do tego samego punktu po prawej stronie - do minus nieskończoności.

Oznacza to, że cała dziedzina definicji tej funkcji jest podzielona na 3 przedziały (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .

Na pierwszym z nich otrzymaliśmy funkcję y \u003d 2 grzech x 2 - 4. Ponieważ - 1 ≤ grzech x ≤ 1 , otrzymujemy:

1 ≤ grzech x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

Oznacza to, że w tym przedziale (- ∞ ; - 3 ] zbiór wartości funkcji wynosi [ - 6 ; 2 ] .

Na półprzedziale (- 3 ; 3 ] otrzymujemy stałą funkcję y = - 1. W konsekwencji cały zestaw jej wartości w tym przypadku zostanie zredukowany do jednej liczby - 1 .

Na drugim interwale 3 ; + ∞ mamy funkcję y = 1 x - 3 . Jest malejąca, ponieważ y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

granica x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ granica x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Stąd zbiorem wartości pierwotnej funkcji dla x > 3 jest zbiór 0; +∞ . Teraz połączmy wyniki: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; +∞ .

Odpowiadać: mi (y) = - 6; - 2 ∪ - 1 ∪ 0 ; +∞ .

Rozwiązanie pokazano na wykresie:

Przykład 12

Warunek: istnieje funkcja y = x 2 - 3 e x . Określ zbiór jego wartości.

Rozwiązanie

Jest zdefiniowany dla wszystkich wartości argumentów, które są liczbami rzeczywistymi. Ustalmy, w jakich odstępach ta funkcja będzie rosła, a w jakich maleje:

y "= x 2 - 3 mi x" = 2 x mi x - mi x (x 2 - 3) mi 2 x = - x 2 + 2 x + 3 mi x = - (x + 1) (x - 3) mi x

Wiemy, że pochodna będzie równa 0, jeśli x = - 1 i x = 3 . Umieszczamy te dwa punkty na osi i sprawdzamy, jakie znaki będzie miała pochodna na otrzymanych przedziałach.

Funkcja zmniejszy się o (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) i wzrośnie o [ - 1 ; 3]. Punktem minimalnym będzie - 1 , maksimum - 3 .

Teraz znajdźmy odpowiednie wartości funkcji:

y (- 1) = - 1 2 - 3 mi - 1 = - 2 mi y (3) = 3 2 - 3 mi 3 = 6 mi - 3

Przyjrzyjmy się zachowaniu funkcji w nieskończoności:

lim x → - ∞ x 2 - 3 mi x = - ∞ 2 - 3 mi - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 mi x = + ∞ 2 - 3 mi + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 "e x" = lim x → + ∞ 2 x mi x = + ∞ + ∞ = = lim x → + ∞ 2 x "(e x)" = 2 lim x → + ∞ 1 mi x = 2 1 + ∞ = + 0

Do obliczenia drugiej granicy wykorzystano regułę L'Hospitala. Narysujmy nasze rozwiązanie na wykresie.

Pokazuje, że wartości funkcji będą maleć od plus nieskończoności do - 2 e, gdy argument zmieni się z minus nieskończoności na - 1 . Jeśli zmieni się z 3 na plus nieskończoność, wówczas wartości zmniejszą się z 6 e - 3 do 0, ale 0 nie zostanie osiągnięte.

Zatem mi (y) = [ - 2 e ; +∞) .

Odpowiadać: mi (y) = [ - 2 mi ; +∞)

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter