D (f)- những giá trị mà đối số có thể nhận, tức là phạm vi chức năng.

E (f)- những giá trị mà hàm có thể nhận, tức là tập hợp các giá trị hàm.

Phương pháp tìm khoảng của hàm.

tìm kiếm tuần tự các giá trị của các đối số hàm phức tạp;

phương pháp cho điểm / ranh giới;

sử dụng các tính chất của tính liên tục và tính đơn điệu của một hàm số;

sử dụng một đạo hàm;

sử dụng các giá trị lớn nhất và nhỏ nhất của hàm;

phương pháp đồ họa;

phương pháp giới thiệu tham số;

phương pháp hàm nghịch đảo.

Chúng ta hãy xem xét một số trong số họ.

Sử dụng đạo hàm

Cách tiếp cận chungđể tìm tập giá trị của hàm liên tục f (x) là tìm giá trị lớn nhất và nhỏ nhất của hàm f (x) trong miền của nó (hoặc để chứng minh rằng một hoặc cả hai đều không tồn tại) .

Nếu bạn cần tìm tập giá trị của một hàm trên phân khúc:

tìm đạo hàm của hàm số đã cho f ”(x);

tìm các điểm tới hạn của hàm số f (x) và chọn các điểm đó thuộc đoạn đã cho;

tính toán các giá trị của hàm tại các đầu đoạn và tại các điểm tới hạn đã chọn;

trong số các giá trị tìm được, chọn giá trị nhỏ nhất và lớn nhất;

Tập hợp các giá trị của hàm được kết luận giữa các giá trị này.

Nếu phạm vi của chức năng là khoảng thời gian, thì cùng một lược đồ được sử dụng, nhưng thay vì các giá trị ở cuối, các giới hạn của hàm được sử dụng khi đối số có xu hướng về cuối khoảng. Giá trị giới hạn từ không được bao gồm trong bộ giá trị.

Phương pháp biên / điểm

Để tìm tập giá trị của hàm, trước tiên hãy tìm tập giá trị đối số, sau đó tìm giá trị nhỏ nhất và lớn nhất tương ứng của hàm hàm. Sử dụng các bất đẳng thức - xác định các ranh giới.

Bản chất là ước lượng hàm liên tục từ bên dưới và từ bên trên và chứng minh rằng hàm đạt đến giới hạn dưới và giới hạn trên của các ước lượng. Trong trường hợp này, sự trùng hợp của tập giá trị của hàm với khoảng từ giới hạn dưới của ước lượng đến giới hạn trên được xác định bởi tính liên tục của hàm và sự vắng mặt của các giá trị khác cho nó.

Các thuộc tính của một hàm liên tục

Một phương án khác là biến hàm thành hàm đơn điệu liên tục, sau đó sử dụng các tính chất của bất đẳng thức, ước lượng tập giá trị của hàm vừa thu được.

Tuần tự tìm giá trị của đối số hàm phức

Dựa trên tìm kiếm tuần tự để tìm tập giá trị của các hàm trung gian tạo nên hàm

Phạm vi của các chức năng cơ bản cơ bản

Hàm số	Nhiều giá trị
$ y = kx + b $	E (y) = (-∞; + ∞)
$ y = x ^ (2n) $	E (y) =
$ y = \ cos (x) $	E (y) = [-1; 1]
$ y = (\ rmtg) \, x $	E (y) = (-∞; + ∞)
$ y = (\ rm ctg) \, x $	E (y) = (-∞; + ∞)
$ y = \ arcsin (x) $	E (y) = [-π / 2; π / 2]
$ y = \ arccos (x) $	E (y) =
$ y = (\ rm arctg) \, x $	E (y) = (-π / 2; π / 2)
$ y = (\ rm arcctg) \, x $	E (y) = (0; π)

Các ví dụ

Tìm tập giá trị của hàm:

Sử dụng đạo hàm

Tìm miền xác định: D (f) = [- 3; 3], vì $ 9-x ^ (2) \ geq 0 $

Tìm đạo hàm: $ f "(x) = - \ frac (x) (\ sqrt (9-x ^ (2))) $

f "(x) = 0 nếu x = 0. f" (x) không tồn tại nếu $ \ sqrt (9-x ^ (2)) = 0 $ tức là cho x = ± 3. Chúng tôi nhận được ba điểm tới hạn: x 1 \ u003d -3, x 2 \ u003d 0, x 3 \ u003d 3, hai trong số đó trùng với các đầu của đoạn. Tính: f (–3) = 0, f (0) = 3, f (3) = 0. Như vậy, giá trị nhỏ nhất của f (x) là 0, giá trị lớn nhất là 3.

Đáp số: E (f) =.

KHÔNG sử dụng phái sinh

Tìm giá trị lớn nhất và nhỏ nhất của hàm số:

Kể từ khi $
f (x) = 1- \ cos ^ (2) (x) + \ cos (x) - \ frac (1) (2) =
= 1- \ frac (1) (2) + \ frac (1) (4) - (\ cos ^ (2) (x) -2 \ cdot \ cos (x) \ cdot \ frac (1) (2) + (\ frac (1) (2)) ^ 2) =
= \ frac (3) (4) - (\ cos (x) - \ frac (1) (2)) ^ (2) $, thì:

$ f (x) \ leq \ frac (3) (4) $ với mọi x;

$ f (x) \ geq \ frac (3) (4) - (\ frac (3) (2)) ^ (2) = - \ frac (3) (2) $ với mọi x (vì $ | \ cos (x) | \ leq 1 $);

$ f (\ frac (\ pi) (3)) = \ frac (3) (4) - (\ cos (\ frac (\ pi) (3)) - \ frac (1) (2)) ^ (2 ) = \ frac (3) (4) $;

$ f (\ pi) = \ frac (3) (4) - (\ cos (\ pi) - \ frac (1) (2)) ^ (2) = - \ frac (3) (2) $;

Trả lời: $ \ frac (3) (4) $ và $ - \ frac (3) (2) $

Nếu bạn giải quyết vấn đề này với sự trợ giúp của đạo hàm, thì bạn sẽ cần phải vượt qua những trở ngại liên quan đến thực tế là hàm f (x) được xác định không phải trên một đoạn mà trên toàn bộ đường thực.

Sử dụng phương pháp giới hạn / ước tính

Nó tuân theo định nghĩa của sin rằng $ -1 \ leq \ sin (x) \ leq 1 $. Tiếp theo, chúng ta sử dụng các tính chất của bất đẳng thức số.

$ -4 \ leq - 4 \ sin (x) \ leq 4 $, (nhân cả ba phần của bất đẳng thức kép với -4);

$ 1 \ leq 5 - 4 \ sin (x) \ leq 9 $ (thêm vào ba phần của bất đẳng thức kép 5);

Vì hàm này liên tục trên toàn bộ miền định nghĩa, tập giá trị của nó nằm giữa giá trị nhỏ nhất và lớn nhất của nó trên toàn bộ miền định nghĩa, nếu có.

Trong trường hợp này, tập giá trị của hàm $ y = 5 - 4 \ sin (x) $ là tập hợp.

Từ các bất đẳng thức $$ \\ -1 \ leq \ cos (7x) \ leq 1 \\ -5 \ leq 5 \ cos (x) \ leq 5 $$, chúng ta thu được ước tính $$ \\ -6 \ leq y \ leq 6 $ $

Đối với x = p và x = 0, hàm nhận các giá trị -6 và 6, tức là đạt đến giới hạn dưới và giới hạn trên. Là sự kết hợp tuyến tính của các hàm liên tục cos (7x) và cos (x), hàm y liên tục dọc theo toàn bộ trục số, do đó, theo tính chất của hàm liên tục, nó nhận tất cả các giá trị từ -6 đến 6, và chỉ có chúng, vì do sự bất bình đẳng $ - 6 \ leq y \ leq 6 $ các giá trị khác là không thể cho nó.

Do đó, E (y) = [-6; 6].

$$ \\ -1 \ leq \ sin (x) \ leq 1 \\ 0 \ leq \ sin ^ (2) (x) \ leq 1 \\ 0 \ leq2 \ sin ^ (2) (x) \ leq 2 \\ 1 \ leq1 + 2 \ sin ^ (2) (x) \ leq 3 $$ Trả lời: E (f) =.

$$ \\ - \ infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ - \ infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

Hãy để chúng tôi biến đổi biểu thức $$ \\ \ sin (x) + \ cos (x) = \ sin (x) + \ sin (\ frac (\ pi) (2) - x) = \\ 2 \ sin \ left ((\ frac (x + \ frac (\ pi) (2) - x) (2)) \ phải) \ cos \ left ((\ frac (x + \ frac (\ pi) (2) + x) ( 2)) \ right) \\ = 2 \ sin (\ frac (\ pi) (4)) cos (x + \ frac (\ pi) (4)) = \ sqrt (2) cos (x + \ frac ( \ pi) (4)) $$.

Định nghĩa của cosine ngụ ý $$ \\ -1 \ leq \ cos (x) \ leq 1; \\ -1 \ leq \ cos ((x + \ frac (\ pi) (4))) \ leq 1; \\ - \ sqrt (2) \ leq \ sqrt (2) \ cos ((x + \ frac (\ pi) (4))) \ leq \ sqrt (2); $$

Vì hàm này liên tục trên toàn bộ miền định nghĩa, nên tập giá trị của nó được bao giữa giá trị nhỏ nhất và lớn nhất của nó, nếu có, tập giá trị của hàm $ y = \ sqrt (2) \ cos ((x + \ frac (\ pi) (4))) $ là tập $ [- \ sqrt (2); \ sqrt (2)] $.

$$ \\ E (3 ^ (x)) = (0; + ∞), \\ E (3 ^ (x) + 1) = (1; + ∞), \\ E (- (3 ^ (x) ) + 1) ^ (2) = (-∞; -1), \\ E (5 - (3 ^ (x) +1) ^ (2)) = (-∞; 4) $$

Ký hiệu $ t = 5 - (3 ^ (x) +1) ^ (2) $, trong đó -∞≤t≤4. Do đó, bài toán được rút gọn thành việc tìm tập giá trị của hàm $ y = \ log_ (0,5) (t) $ trên tia (-∞; 4). Vì hàm $ y = \ log_ (0,5) (t) $ chỉ được xác định cho t> 0, tập giá trị của nó trên tia (-∞; 4) trùng với tập giá trị của hàm số trên khoảng (0; 4) biểu diễn là giao điểm của tia (-∞; 4) với miền xác định (0; + ∞) của hàm số lôgarit. Trên khoảng (0; 4) hàm số này liên tục và giảm dần. Đối với t> 0, nó có xu hướng + ∞ và đối với t = 4, nó có giá trị -2, do đó E (y) = (-2, + ∞).

Chúng tôi sử dụng một kỹ thuật dựa trên biểu diễn đồ họa của một hàm.

Sau các phép biến đổi của hàm, ta có: y 2 + x 2 = 25, và y ≥ 0, | x | ≤ 5.

Cần nhắc lại rằng $ x ^ (2) + y ^ (2) = r ^ (2) $ là phương trình của một đường tròn bán kính r.

Theo những hạn chế này, đồ thị của phương trình này là hình bán nguyệt phía trên có tâm tại gốc và bán kính bằng 5. Rõ ràng là E (y) =.

Đáp số: E (y) =.

Người giới thiệu

Phạm vi chức năng trong các nhiệm vụ của Kiểm tra trạng thái thống nhất, Minyuk Irina Borisovna

Mẹo tìm tập giá trị của hàm, Belyaeva I., Fedorova S.

Tìm tập giá trị của hàm

Cách giải các bài toán trong kỳ thi tuyển sinh, I.I. Melnikov, I.N. Sergeev

GBOU lyceum (kinh tế) với. Isakla

Giáo viên toán Kuzaeva V.N.

2016

Những tài liệu tham khảo

Mẫu giải pháp Tìm tập hợp các giá trị của hàm

Phạm vi chức năng
Là

y - bất kỳ số nào

Phạm vi chức năng
Là y - bất kỳ số nào

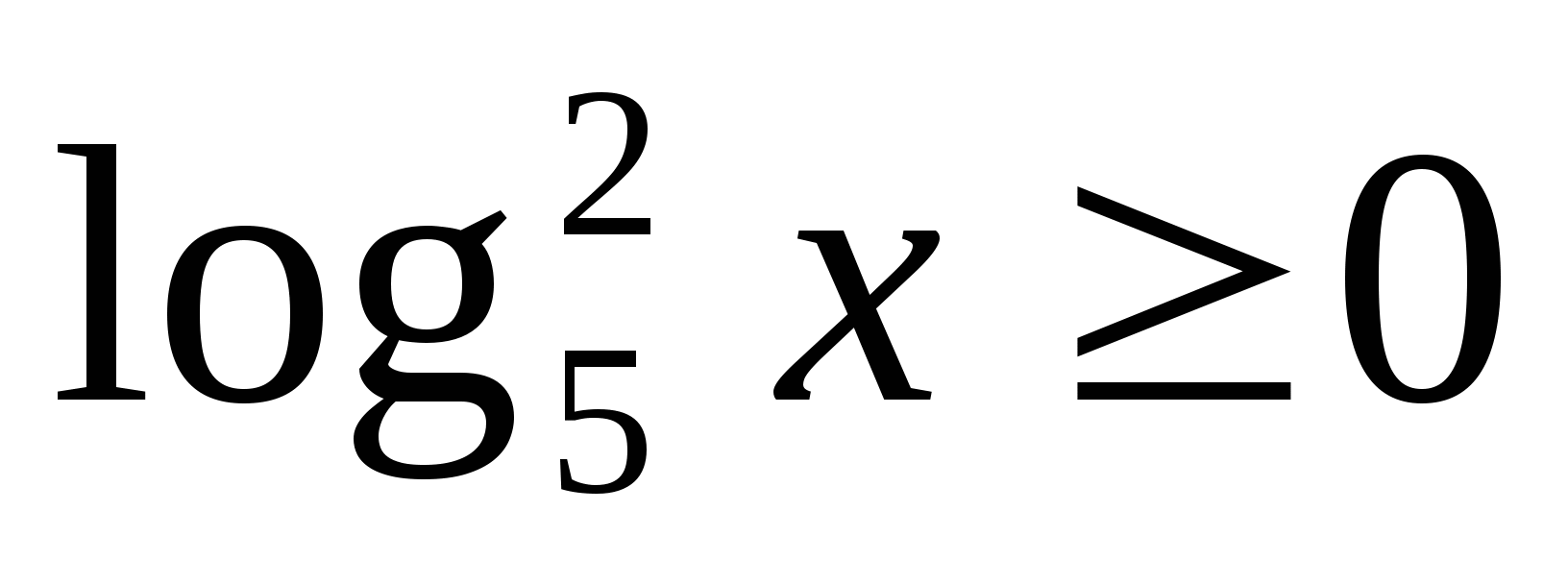
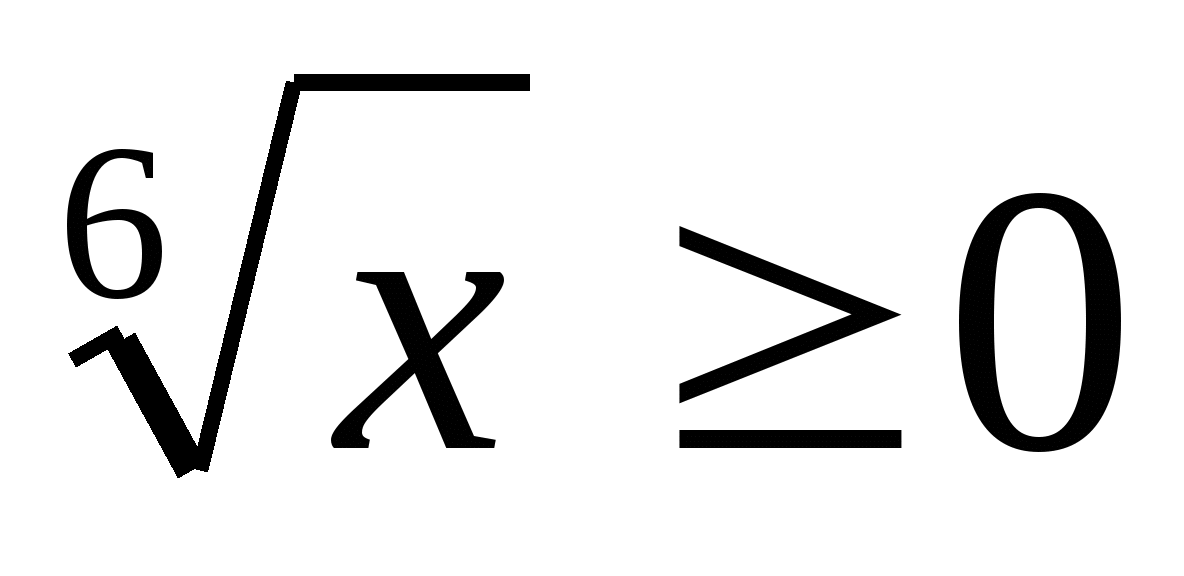
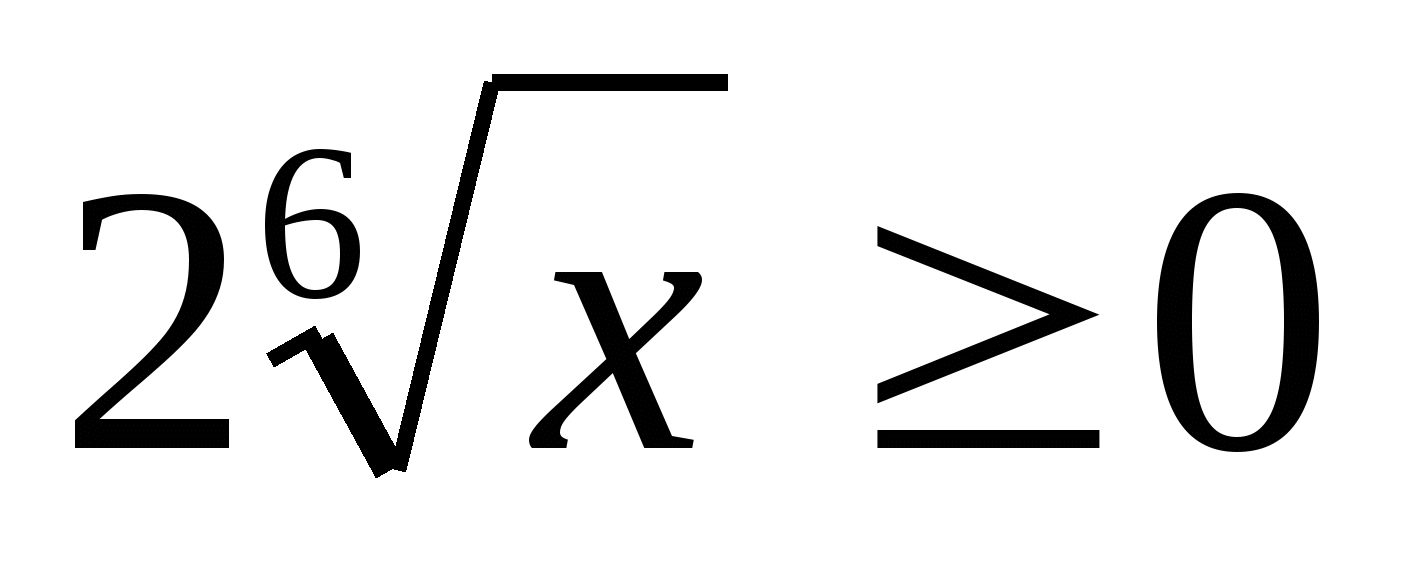
Nhiều giá trị

y - bất kỳ số nào

Giá trị cao nhất

Giá trị thấp nhất

Miền X - bất kỳ số nào
, ở đâu

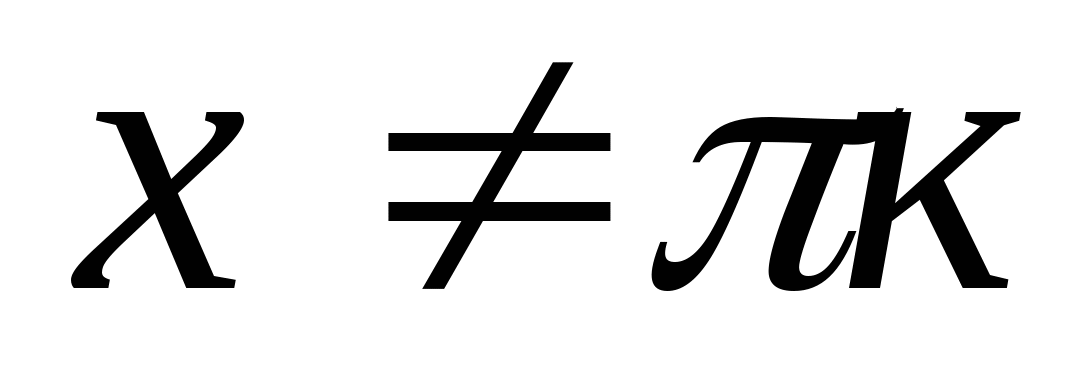, ở đâu

Nhiều giá trị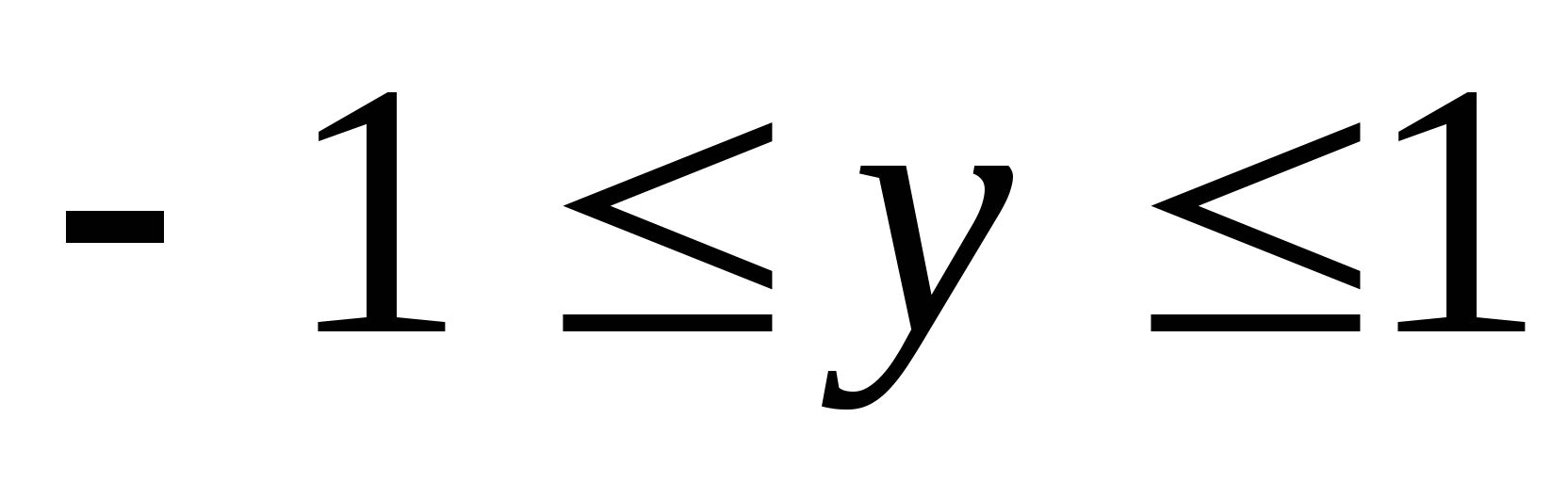
y - bất kỳ số nàoy - bất kỳ số nào

Vẽ các mẫu cho một số hàm lượng giác

Tập hợp các giá trị của hàm lượng giác

lựa chọn 1

Y =tội 3x + 2.

1) (-5;5) 2) 3) 4) (1;5)

2. Tìm diện tích của \ u200b \ u200b của hàm y =tg x + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. Chỉ định số nguyên nhỏ nhất từ ​​phạm vi của hàm

y = 12,7 + 5 tội(3x-2).

1) -5 2) 8 3) 5 4) 17

5. Chỉ định hàm có tập giá trị là đoạn [-2; 2].

1) y = cos 2x 2) y = tội 2 x 3) y = cos 2 x +2

4) y = 2 tội 4 x

6. Tìm tập giá trị của hàmy = tg 2 xtrên phân khúc

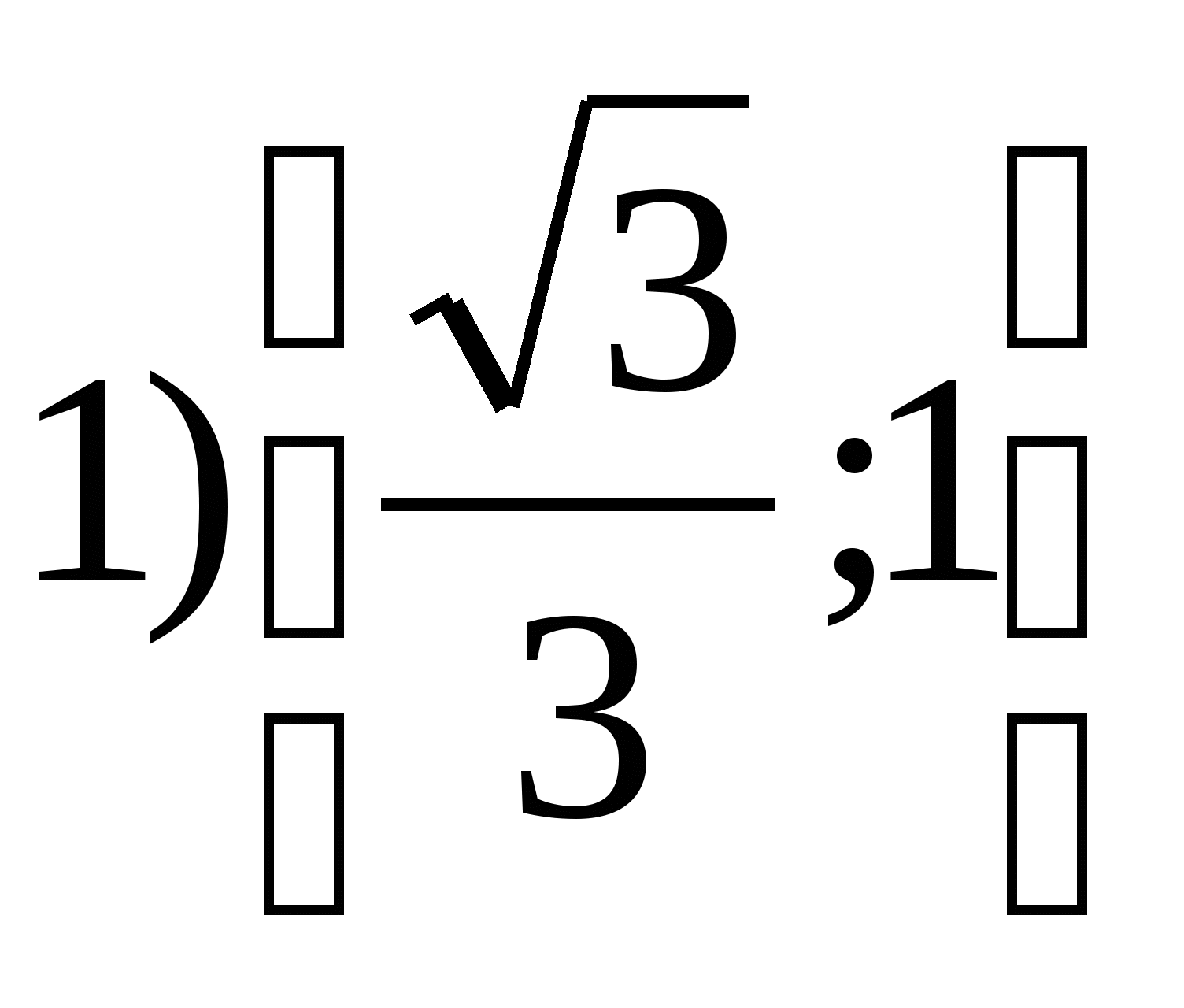
7. Tìm tổng của tất cả các số nguyên nằm trong khoảng của hàmy = 4 cos 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Lựa chọn 2

y = 2 cos 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Tìm phạm vi của hàm

1) 3) (-∞;∞) 4) .

3. Chỉ định số nhỏ nhất từ ​​phạm vi của hàm

1) 4 2) -3 3) 1 4) -7

4. Chỉ định số nguyên lớn nhất từ ​​phạm vi của hàm

1) 2 2) 13 3) 12 4) -2

5. Chỉ định một hàm có tập giá trị là đoạn [-5; 5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Tìm tập giá trị của hàm
trên phân khúc

7. Tìm tích của tất cả các số nguyên trong khoảng của hàm số y \ u003d 5 - 3tội 2 x.

1) 120 2) 14 3) -15 4) 0

Lựa chọn 3
1. Chỉ định một tập hợp các giá trị hàmy = tội 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Xác định số nhỏ nhất trong khoảng của hàm số y = 5tg 2 x+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Chỉ định một hàm có tập giá trị là một đoạn

[-17;-13].

1) y \ u003d 5 sin x - 8 3) y \ u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 sin x +10

6. Cho biết số tự nhiên nhỏ nhất không nằm trong tập giá trị của hàm số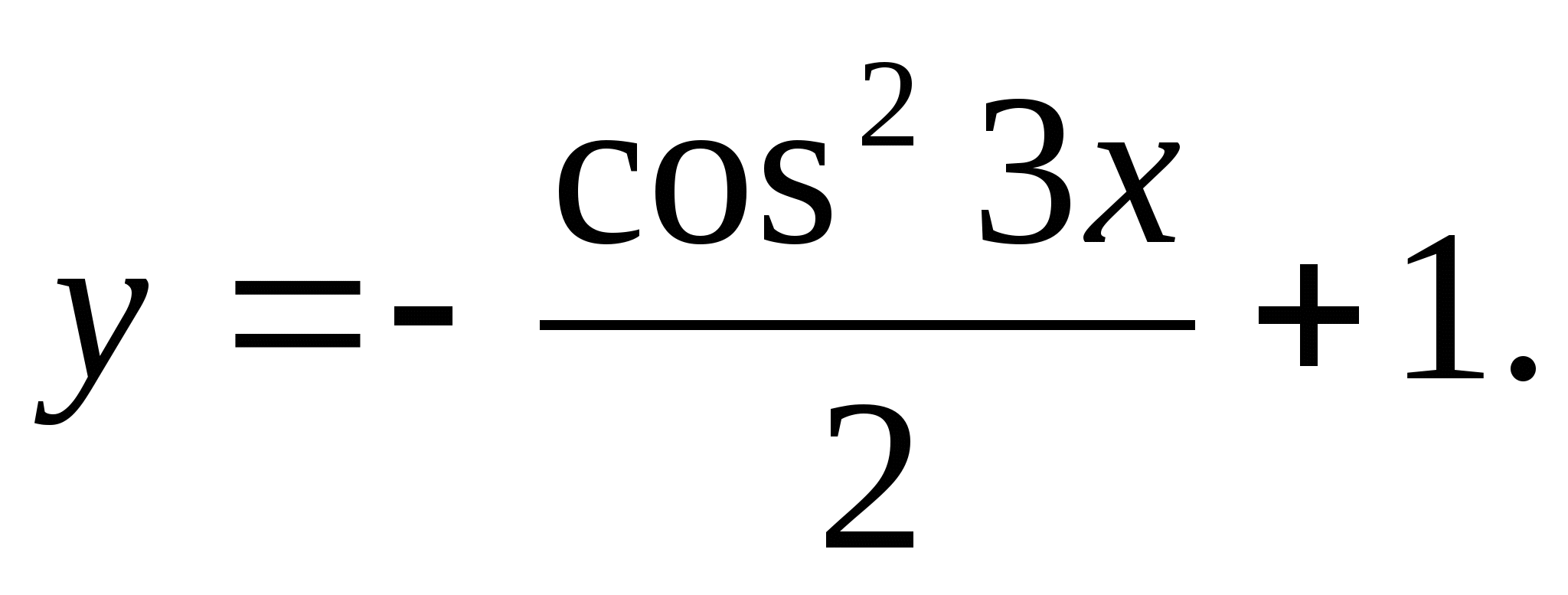

1) 2 2) 4 3) 15 4) 6

7. Có bao nhiêu số nguyên thuộc tập giá trị của hàm số

y = 2 cos 3 x +10?

1) 2 2) 3 3) 4 5) 5

Lựa chọn 4

1) 2) 4) (-7;-6)

2. Tìm khoảng của hàm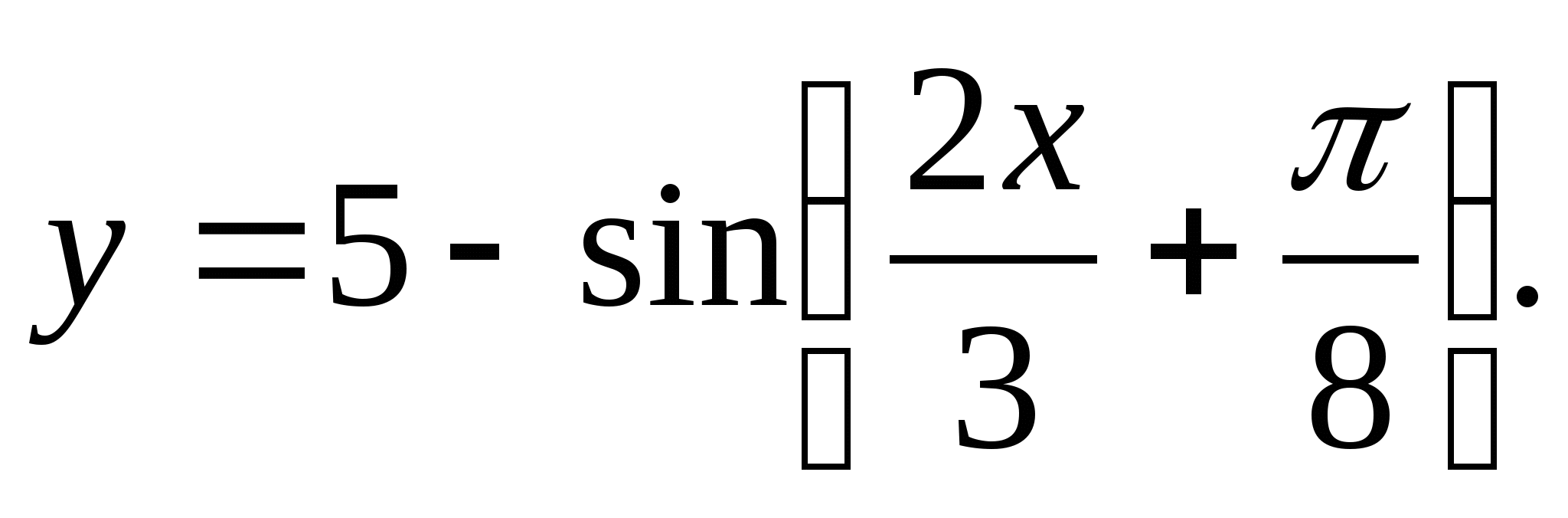

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Chỉ định số lớn nhất từ ​​phạm vi của hàmy = -3 ctg 2 x+7.

1) 10 2) 4 3) 7 4) -3

4. Số nào sau đây không thuộc tập giá trị của hàm số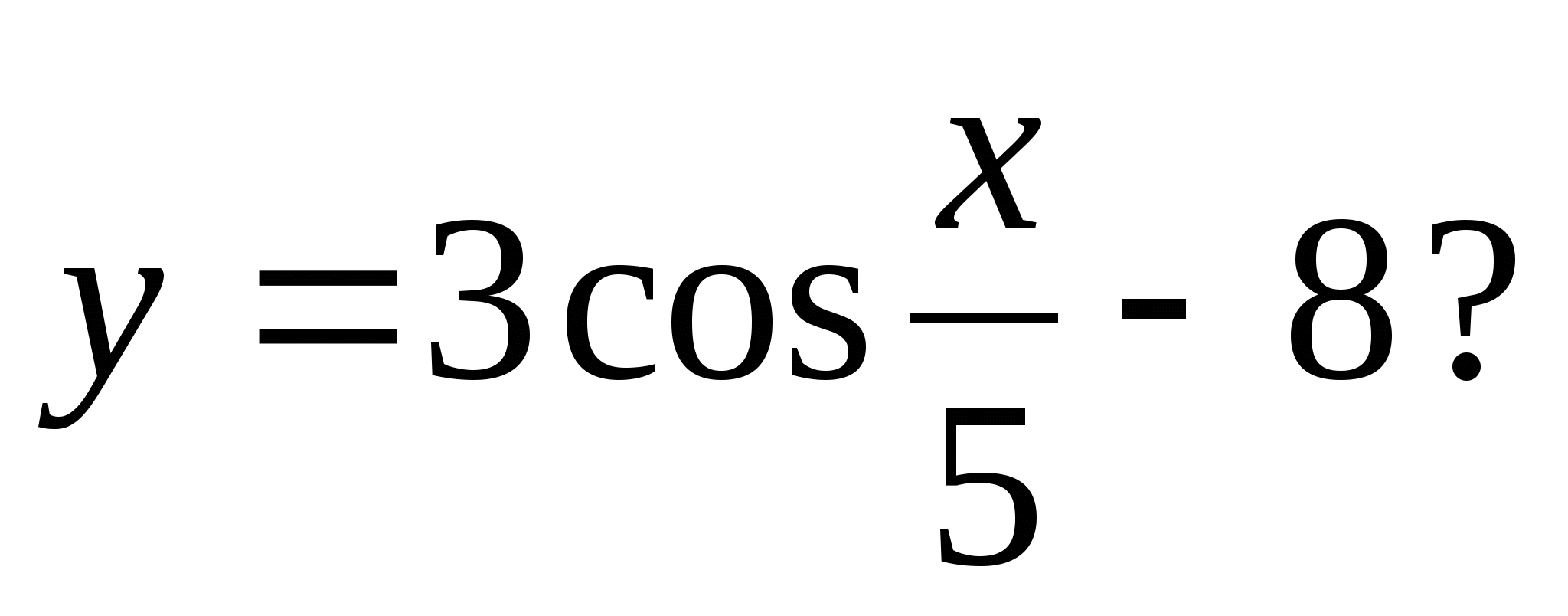

1) -6 2) -5 3) -10 4) -7

5. Chỉ định một hàm có tập giá trị là khoảng.

6. Chỉ định số nguyên âm lớn nhất không có trong phạm vi của hàm

1) -1 2) -25 3) -6 4) -2

7. Có bao nhiêu số nguyên thuộc tập giá trị của hàm số

1) 11 2) 3 3) 5 4) 4

Lựa chọn 5

1. Xác định tập giá trị của hàm số y = 2 -tội 5 x.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Tìm khoảng của hàm

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Chỉ định số nguyên nhỏ nhất từ ​​phạm vi của hàm

y = 3 + tội 2 2 x.

1) 0 2) 1 3) 3 4) 4

4. Số nào sau đây thuộc tập giá trị của hàm số

1) 128 2) 10,5 3) 3 4) -235

5. Chỉ định hàm có tập giá trị là đoạn [-9; 15].

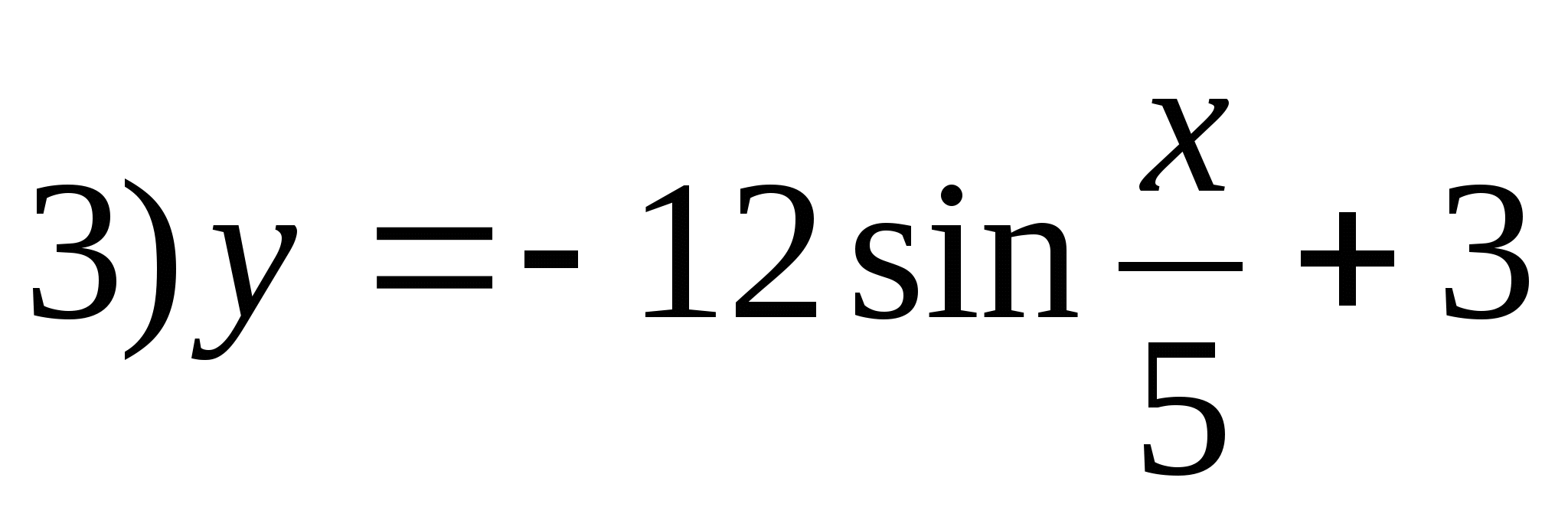
6. Tìm tổng các số nguyên có trong tập giá trị của hàm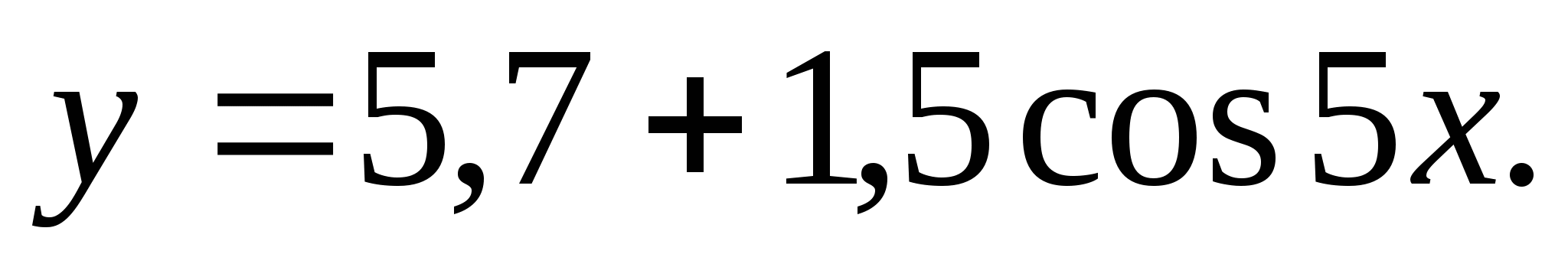

1) 0 2) 7 3) 18 4) 22

7. Tìm giá trị lớn nhất của hàm số
trên phân khúc

1) 0,5 2) 1,5 3) 0 4) 2

Tùy chọn 6

1. Chỉ định đoạn tương ứng với tập giá trị của hàm

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Tìm khoảng của hàm

3. Chỉ định số lớn nhất từ ​​phạm vi của hàm

1) 5 2) -6 3) -3 4) 4

4. Số nào sau đây thuộc tập giá trị của hàm số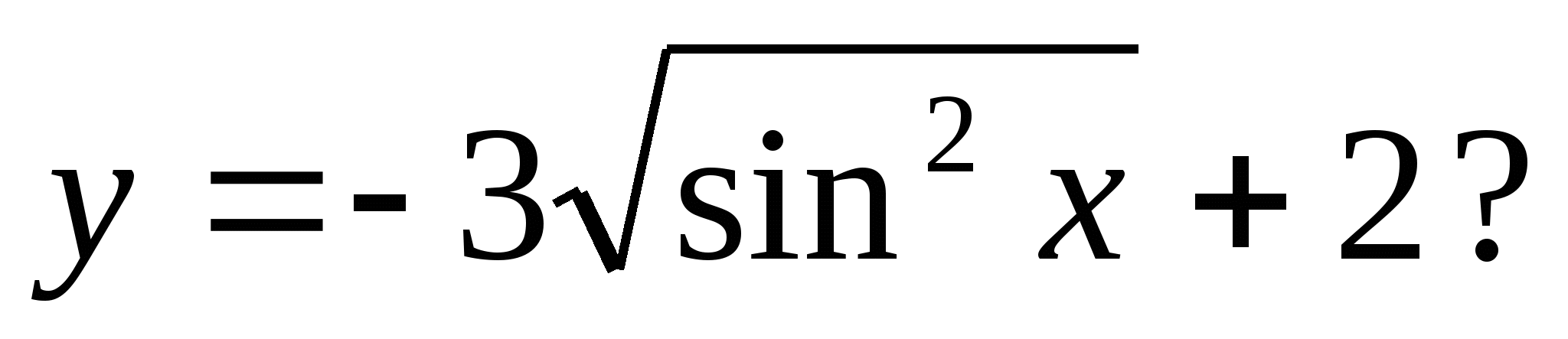

1) 5 2) 0 3) -3 4) 4

5. Chỉ định một hàm có tập giá trị là khoảng.

1) tại = 15 - 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 cos 4 x 4) y = - tg 2 x + 1

6. Tìm tích của các số nguyên có trong tập giá trị

y = 3,8 – 1,4 tội 3 x.

1) 17 2) 12 3) 0 4) 60

7. Tìm tập giá trị của hàm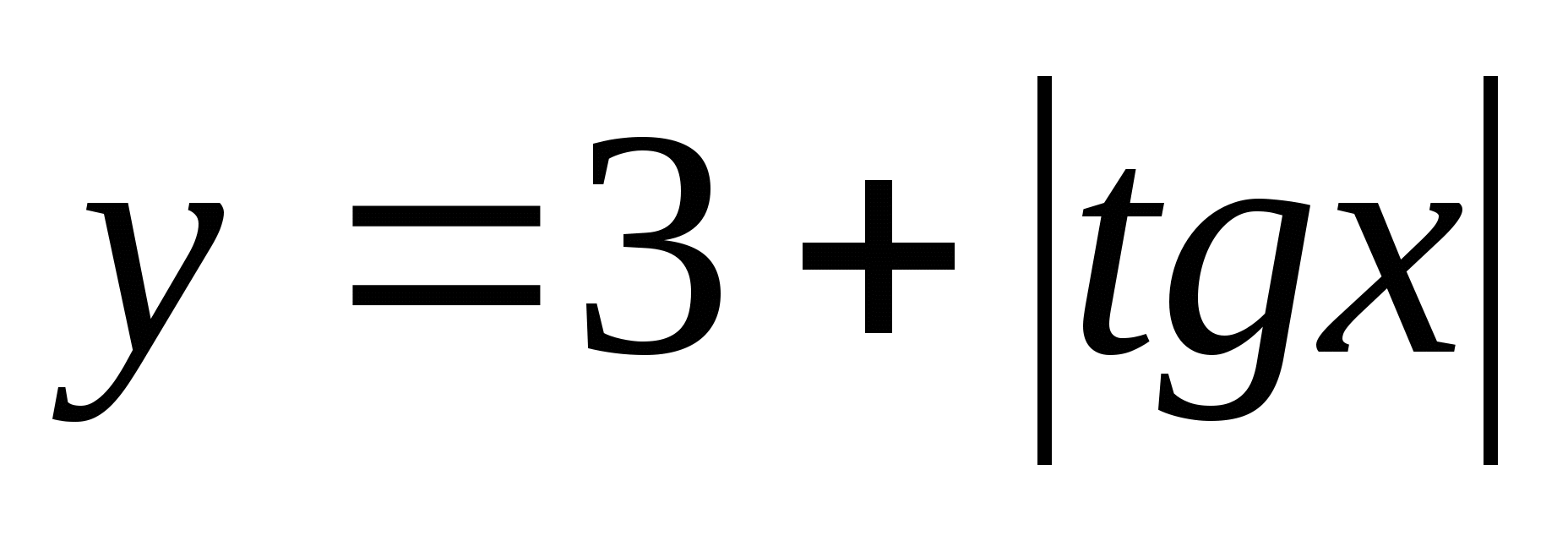
ở giữa

1) (3;4) 2) 3)

Lựa chọn 7

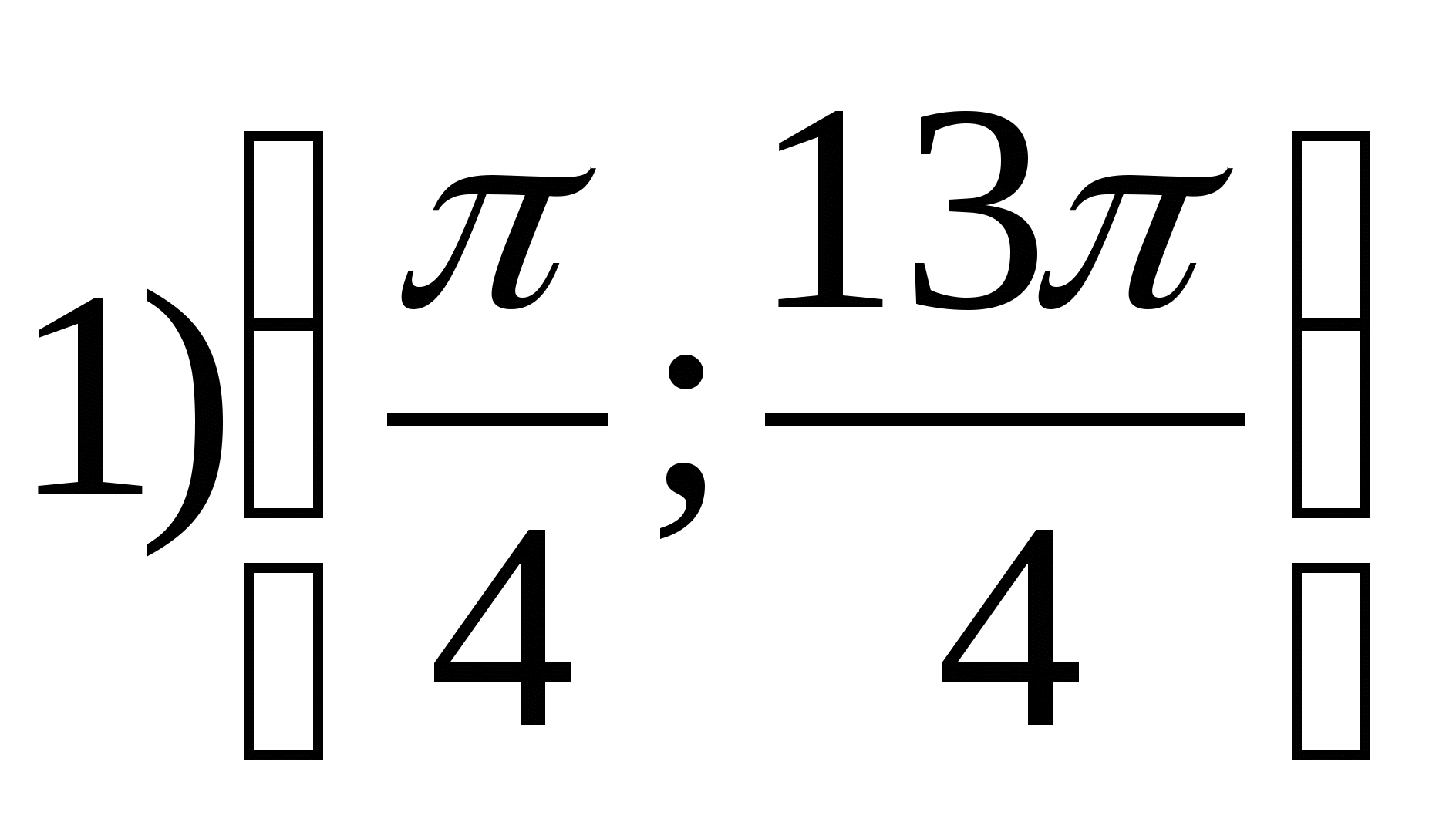
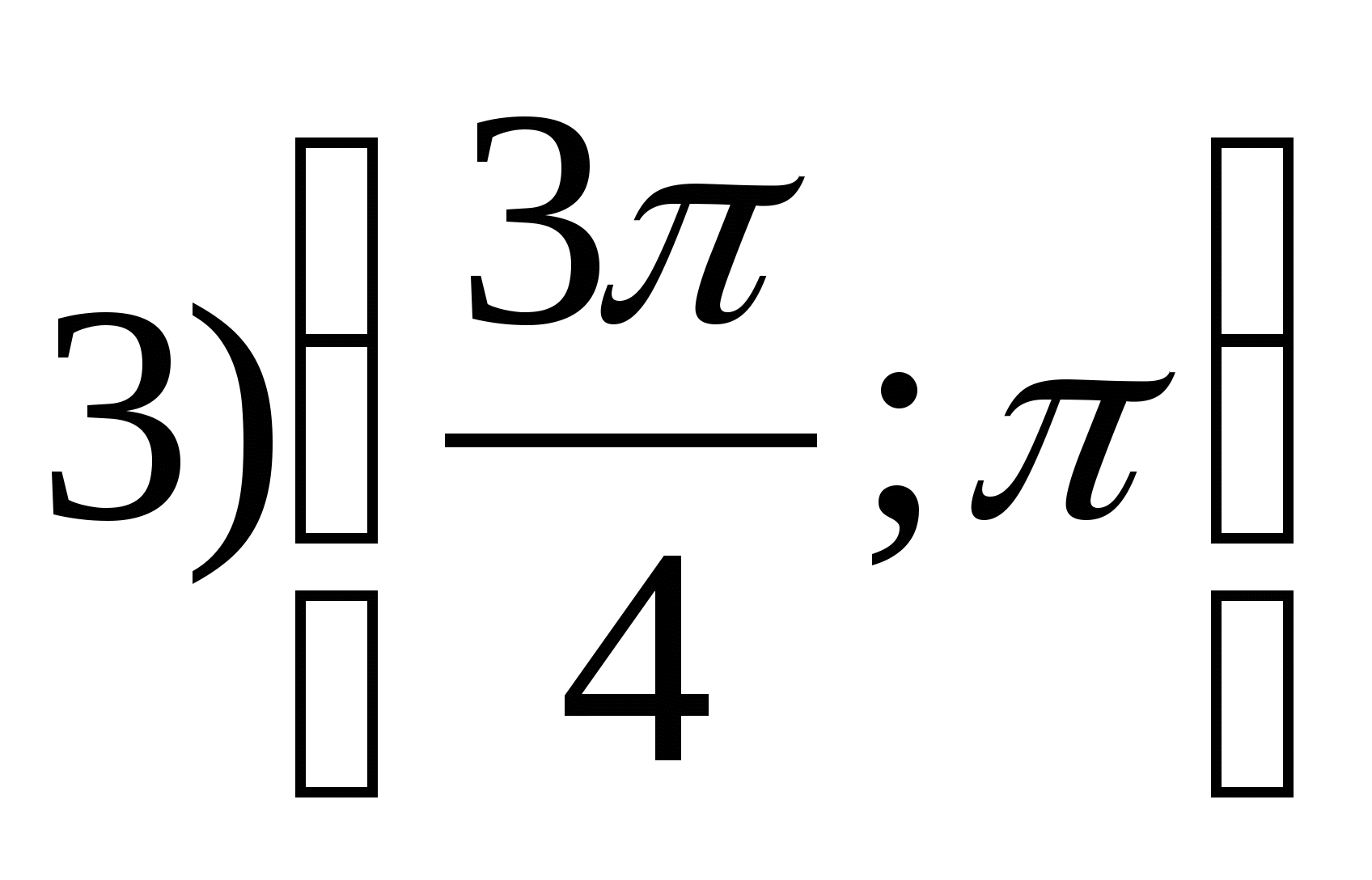
2. Tìm giá trị nguyên nhỏ nhất của hàm số

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. Với những giá trị nào của a thì phương trìnhtội(3 x-4)+5= một tan?

1) 2) 3) (4;6) 4) (-6;4]

tội 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

ở giữa

2) 0 3) 1

y = 4 tội(x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Lựa chọn 8

1. Tìm tập giá trị của hàmy = arctgx- 2π.

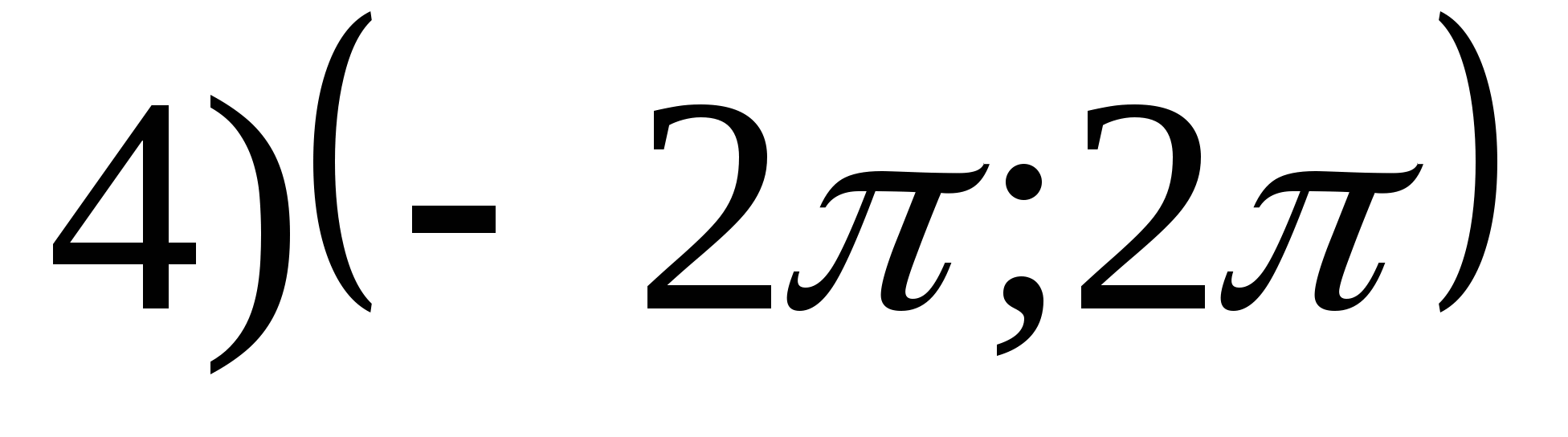
2. Tìm giá trị lớn nhất của hàm số

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Số nào sau đây có thể là giá trị của hàm số

1) -4 2) -2 3) 0 4) 2

4. Với những giá trị nào của p thì phương trình -2+cos(4 x-1)= P có rễ không?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Tìm tập giá trị của hàmy = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

ở giữa
.

1) 0 2) 1 3) -1 4) 3

7. Có bao nhiêu số nguyên trong phạm vi của hàm

1) 4 2) 3 3) 5 4) 2

Tùy chọn 9

1. Tìm khoảng của hàm

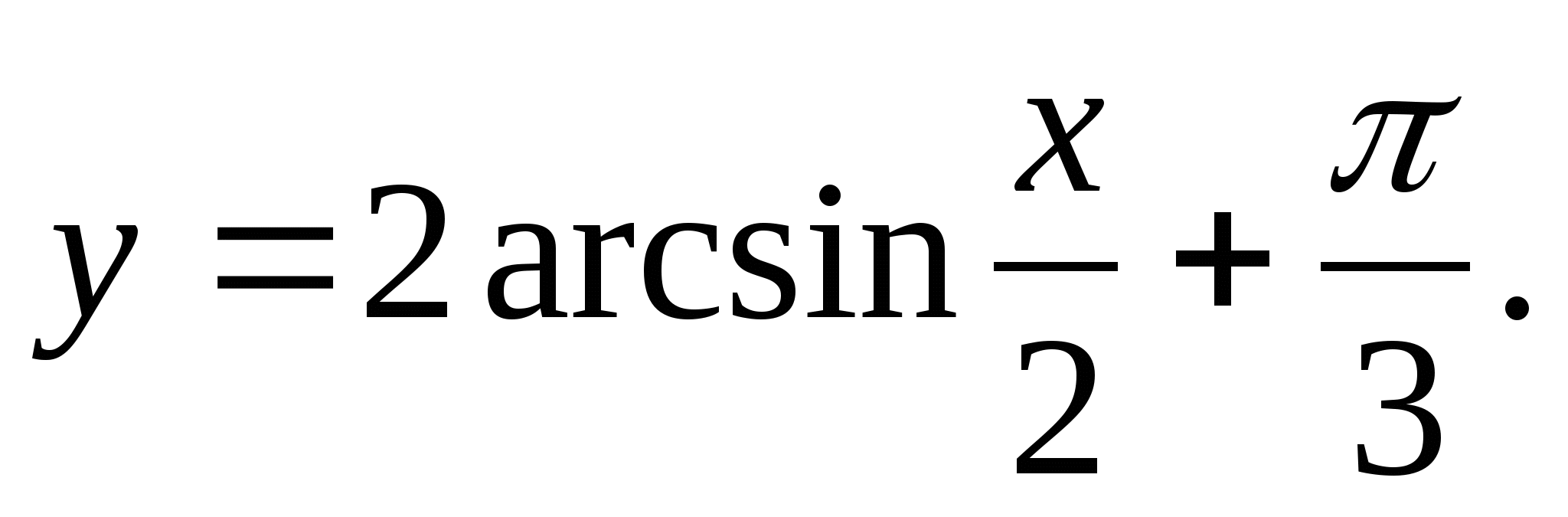
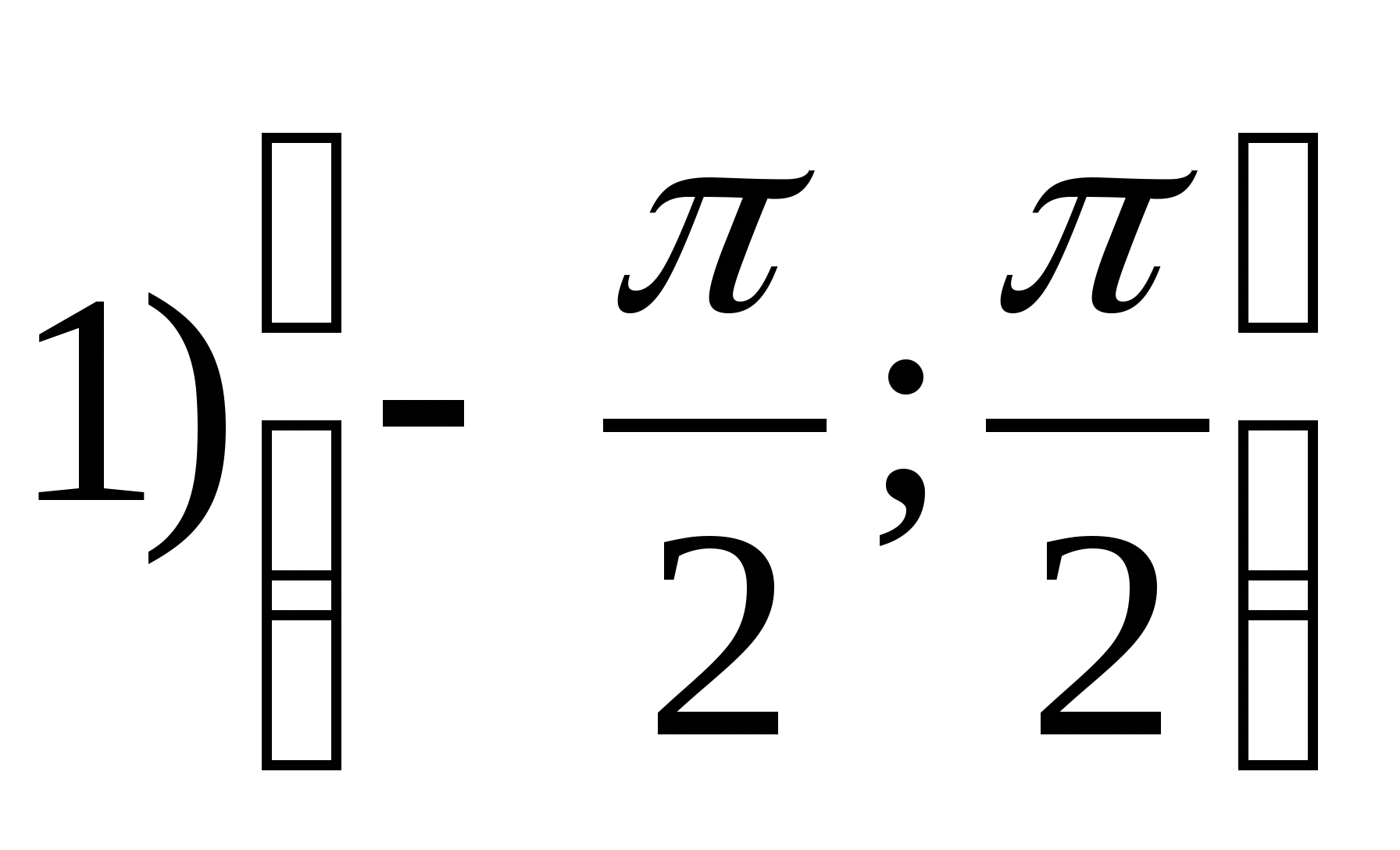
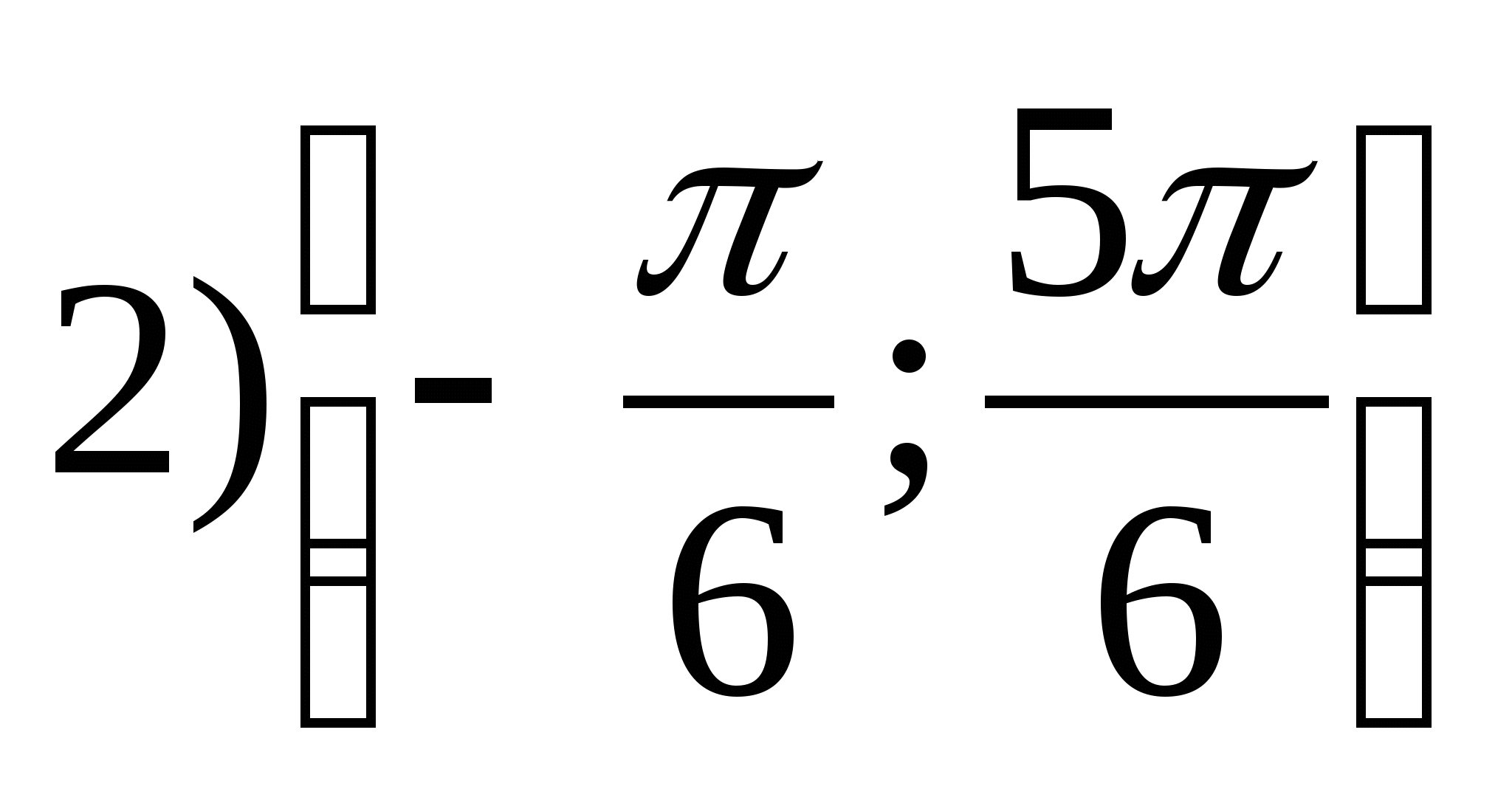
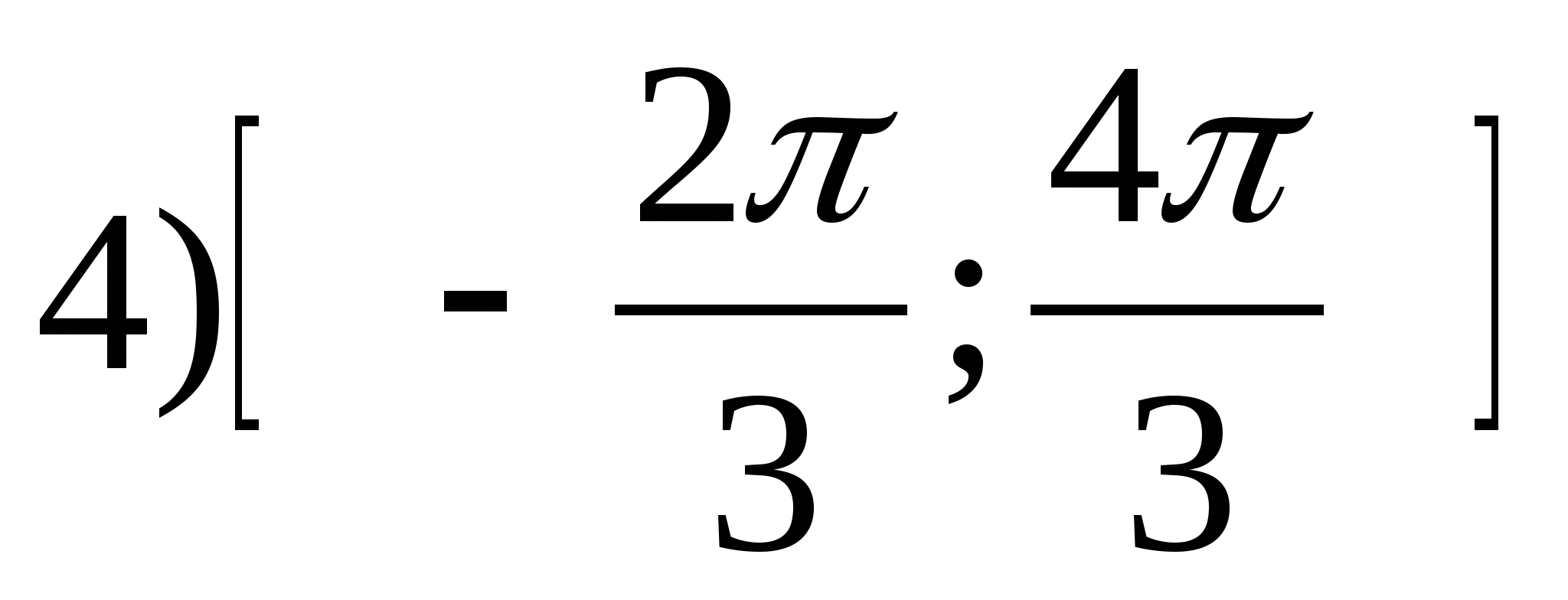
2. Tìm giá trị nguyên lớn nhất của hàm số

1) 4 2) 5 3) 6 4) 7

3. Số nào sau đây có thể là giá trị của hàm số

1) 0 2) 3 3) 6 4) 9

k phương trình - k + tội(2 x-1) = 2 có thể giải được không?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Tìm tập hợp các giá trị hàm \ u200b \ u200bằng \ u003d -cos 2 3 x + 4.

1) 2) 3) 4)

6. Chỉ ra giá trị nhỏ nhất của hàm
ở giữa

2) -1 3) 0 4) 1

7. Tìm bao nhiêu số nguyên trong khoảng của hàm số y = 12cos 3 x +5 tội 3 x.

1) 13 2) 27 3) 26 4) 14

Lựa chọn 10

1. Tìm khoảng của hàm

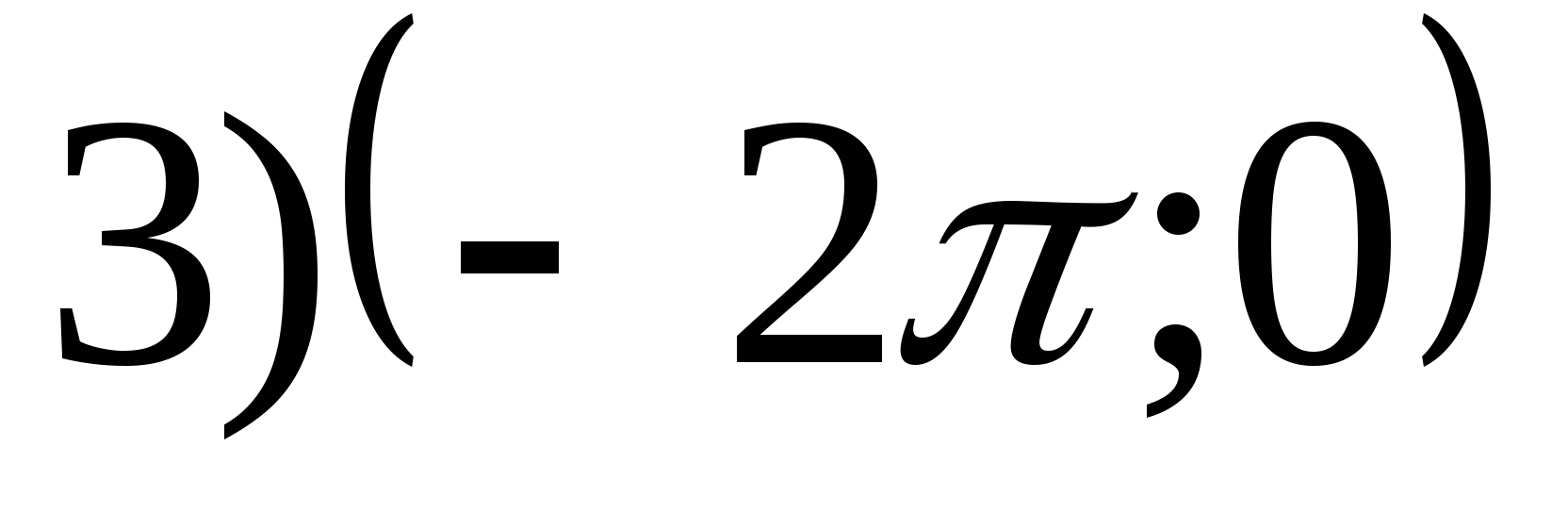
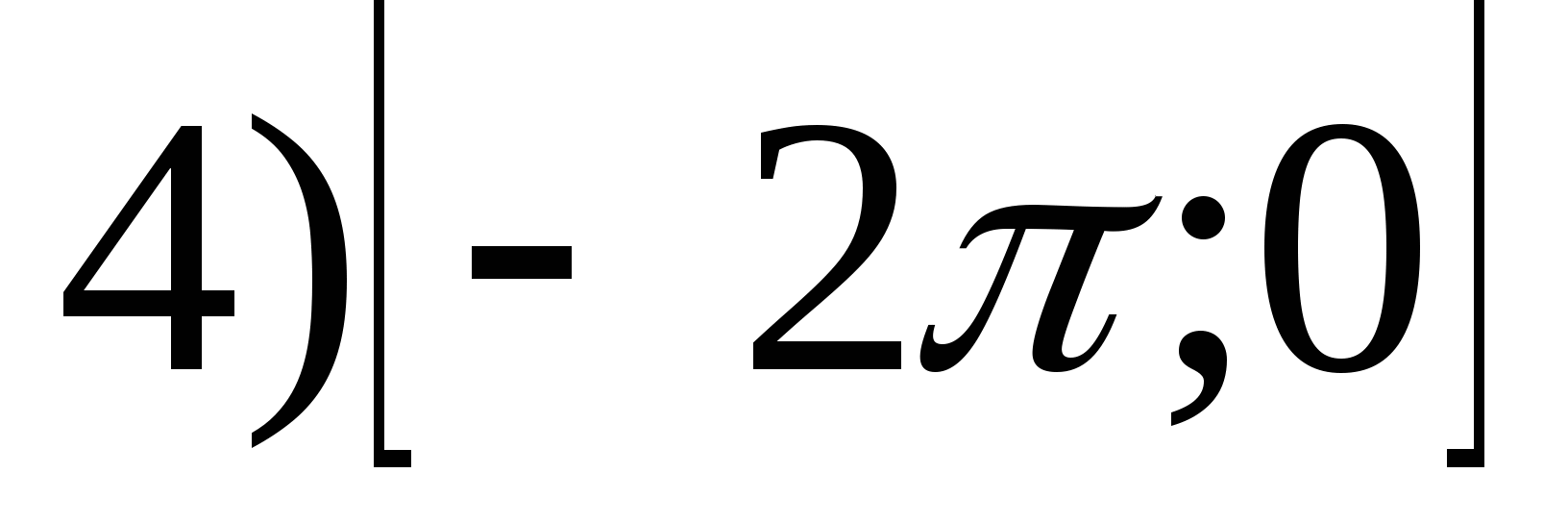
2. Tìm giá trị nhỏ nhất của hàm số

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Số nào sau đây có thể là giá trị của hàm số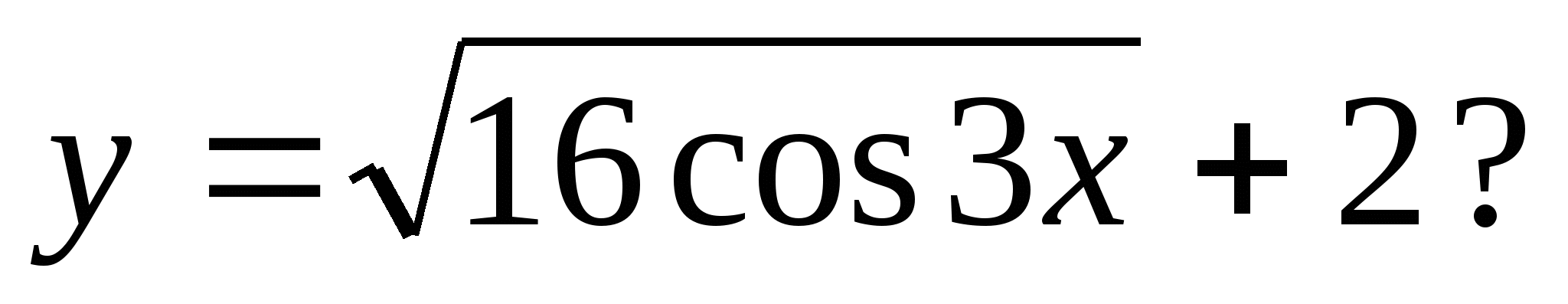

1) -4 2) -1 3) 3 4) 7

4. Các giá trị của tham sốm phương trình cos (3 x + 2)- m= 5 có rễ không?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Tìm tập hợp các giá trị hàm \ u200b \ u200 bằng \ u003d -2ctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Chỉ định giá trị lớn nhất của hàm
ở giữa

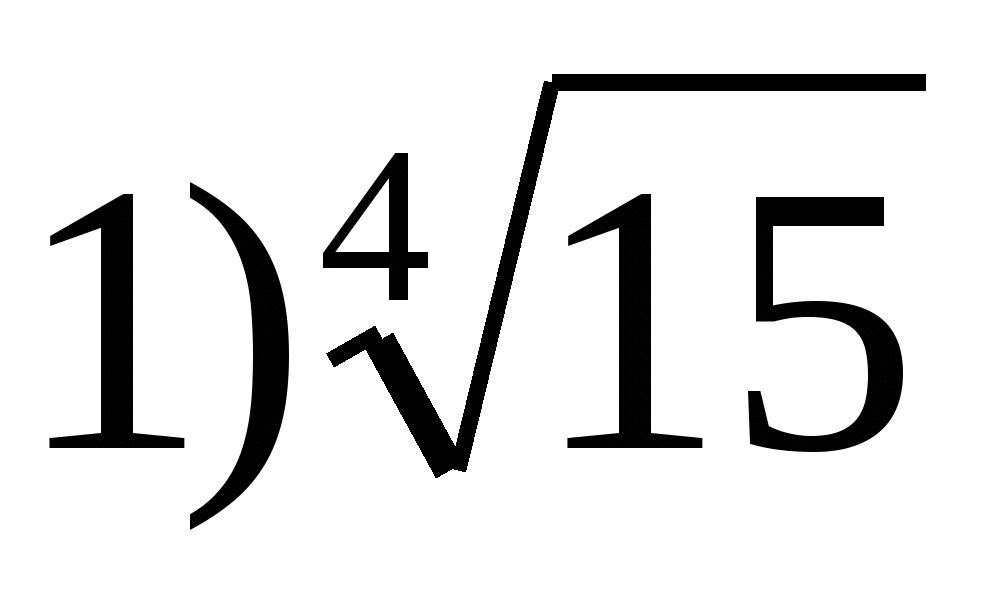2) 0 3) 2 4) 1

7. Tìm có bao nhiêu số nguyên trong phạm vi của hàm

1) 30 2) 35 3) 17 4) 7

Tập hợp các giá trị của hàm số mũ và hàm số lôgarit

lựa chọn 1

1. Tìm khoảng của hàm

1) 4) (-∞;3)

2. Chỉ định một tập hợp các giá trị hàm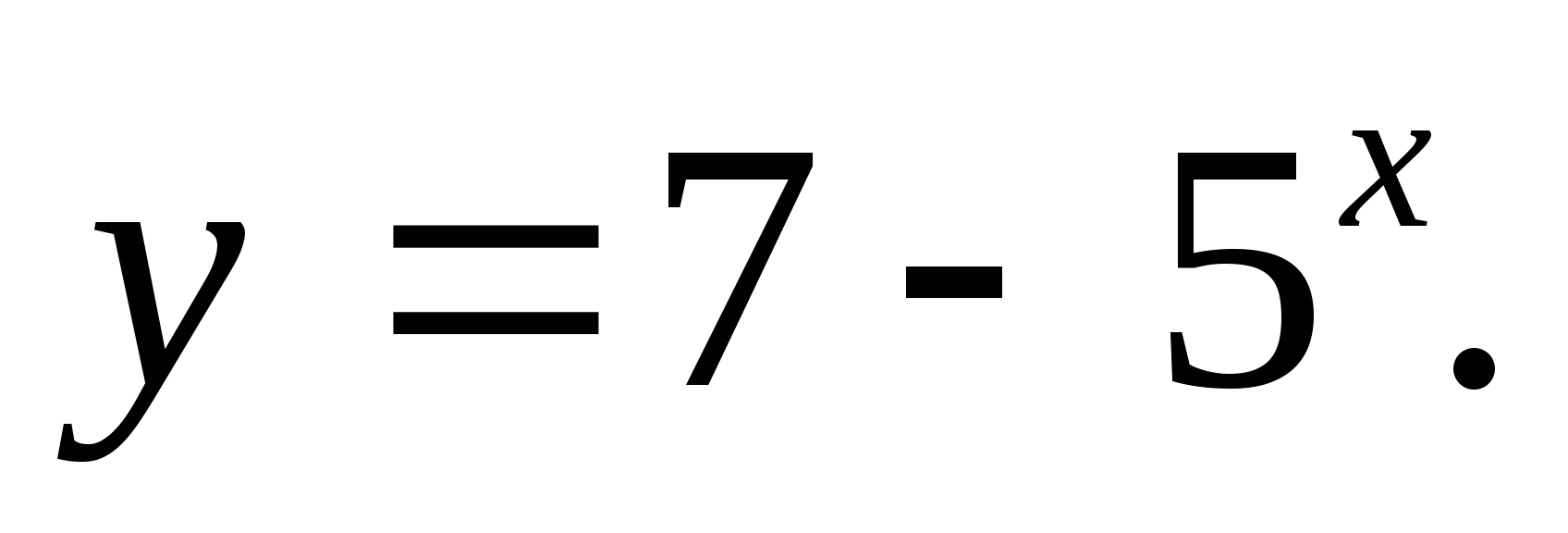

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Chỉ ra giá trị nguyên nhỏ nhất của hàm

1) 1 2) -1 3) 0 4) -5

7. Xác định một hàm số có tập giá trị là khoảng (1; ∞).

Lựa chọn 2

1. Chỉ định một tập hợp các giá trị hàm

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Tìm khoảng của hàm

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Chỉ ra giá trị nguyên nhỏ nhất của hàm

1) -12 2) -11 3) -10 4) -15

4. Chỉ định một số không thuộc tập giá trị của hàm

1) -42 2) 3 3) 1 4) -20

5. Chỉ định một tập hợp các giá trị hàm

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Chỉ định giá trị nguyên lớn nhất của hàm

1) 10 2) 3 3) 9 4) 2

7. Chỉ định một hàm có tập giá trị là khoảng

(-∞;13).

Lựa chọn 5

1. Chỉ ra giá trị nguyên nhỏ nhất của hàm

1) 0 2) -1 3) -2 4) -3

2. Các số sau đây thuộc khoảng nào của hàm số

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Tìm trên đoạn nào hàm
nhận giá trị lớn nhất là 2 và giá trị nhỏ nhất là -3.

1) 2) (-5;2) 3) 4) (-3;2)

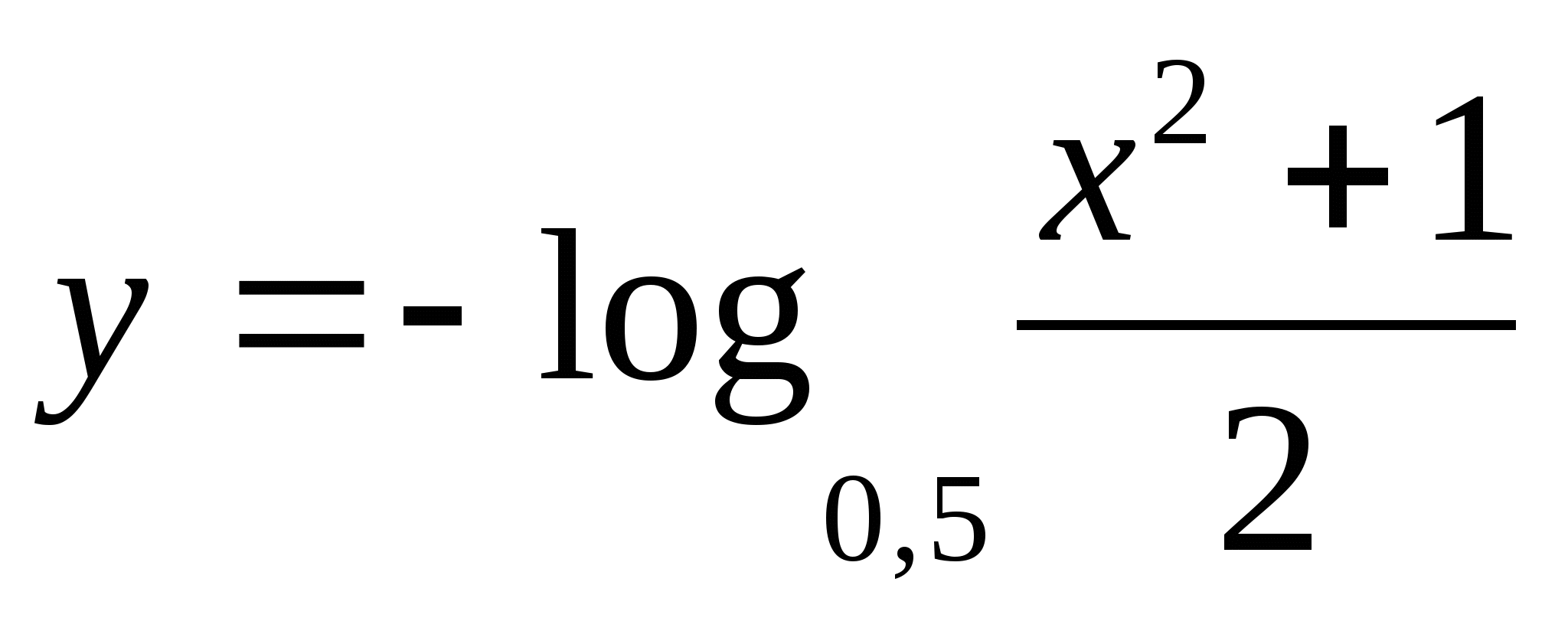ở giữa

1) -1/2 2) 5 3) 2 4) 4

8. Tìm tổng tất cả các số tự nhiên không có trong các tập giá trị của hàm số

1) 3 2) 6 3) 10 4) 8

Tùy chọn 6

1. Chỉ định giá trị nguyên lớn nhất của hàm

1) 2 2) 4 3) 3 4) 5

2. Dãy số nào sau đây không thuộc khoảng của hàm số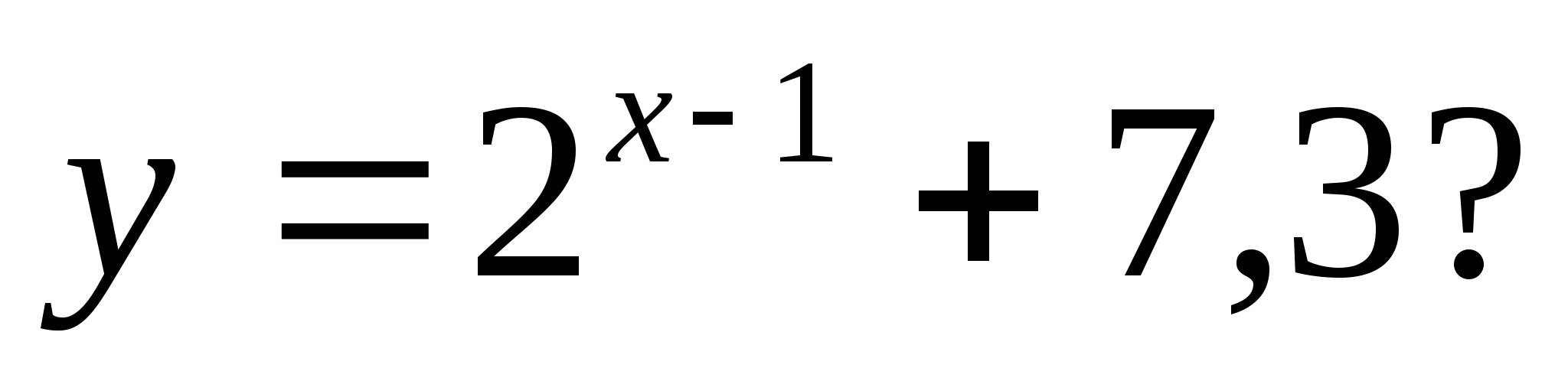

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Chỉ định một tập hợp các giá trị hàm

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Tìm tất cả các điểm trên OU là hình chiếu của các điểm thuộc đồ thị của hàm số

1) (0;∞) 2) 2) (-3;2) 3) [ khúc gỗ 2 3;2] 4) (khúc gỗ 2 3;2)

6. Tìm trên đoạn nào hàm
nhận giá trị nhỏ nhất là -2 và giá trị lớn nhất là 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Chỉ định giá trị lớn nhất của hàm
ở giữa

[-0,9; 0]. 2. Tìm giá trị nhỏ nhất của hàm số trên đoạn.

4. Hàm nhận bao nhiêu giá trị nguyên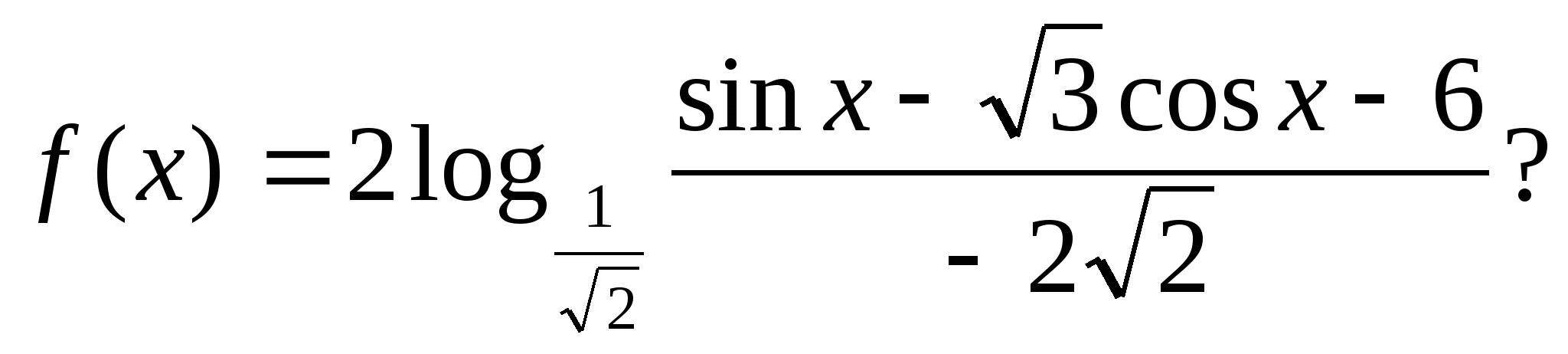

Câu trả lời

Phần 1

Tập hợp các giá trị của hàm số mũ và hàm số lôgarit

Phần 2

Khái niệm về một chức năng và mọi thứ kết nối với nó theo truyền thống rất phức tạp, không được hiểu đầy đủ. Một trở ngại đặc biệt trong việc nghiên cứu hàm số và chuẩn bị cho kỳ thi là miền xác định và khoảng giá trị (thay đổi) của hàm số.
Thông thường, học sinh không thấy sự khác biệt giữa miền của một hàm và miền các giá trị của nó.
Và nếu học sinh quản lý thành thạo các nhiệm vụ tìm miền xác định của một hàm số, thì các nhiệm vụ tìm tập giá trị của một hàm số sẽ gây ra cho họ những khó khăn đáng kể.
Mục đích của bài viết này: làm quen với các phương pháp tìm giá trị của một hàm.
Kết quả của việc xem xét đề tài này, tài liệu lý thuyết đã được nghiên cứu, phương pháp giải các bài toán tìm tập giá trị của hàm số, tài liệu giáo khoa được lựa chọn để làm bài độc lập cho học sinh.
Giáo viên có thể sử dụng bài báo này khi chuẩn bị cho học sinh thi cuối kỳ và thi tuyển sinh, khi nghiên cứu chủ đề “Phạm vi của hàm số” trong các lớp học tùy chọn trong các khóa học môn toán tự chọn.

I. Xác định phạm vi của chức năng.

Diện tích (tập hợp) các giá trị E (y) của hàm số y = f (x) là tập hợp các số y 0, với mỗi số đó có một số x 0 sao cho: f (x 0) = y 0.

Chúng ta hãy nhớ lại phạm vi của các hàm cơ bản chính.

Hãy xem xét một bảng.

Hàm số	Nhiều giá trị
y = kx + b	E (y) = (-∞; + ∞)
y = x2n	E (y) =
y = cos x	E (y) = [-1; 1]
y = tg x	E (y) = (-∞; + ∞)
y = ctg x	E (y) = (-∞; + ∞)
y = arcsin x	E (y) = [-π / 2; π / 2]
y = arcos x	E (y) =
y = arctan x	E (y) = (-π / 2; π / 2)
y = arcctg x	E (y) = (0; π)

Cũng lưu ý rằng phạm vi của bất kỳ đa thức bậc chẵn nào là khoảng, trong đó n là giá trị lớn nhất của đa thức này.

II. Thuộc tính hàm được sử dụng để tìm phạm vi của một hàm

Để tìm thành công tập giá trị của một hàm, người ta phải có kiến ​​thức tốt về các tính chất của các hàm cơ bản cơ bản, đặc biệt là các miền định nghĩa của chúng, phạm vi giá trị và tính chất của tính đơn điệu. Chúng ta hãy trình bày các thuộc tính của hàm phân biệt liên tục, đơn điệu, thường được sử dụng để tìm tập giá trị của hàm.

Thuộc tính 2 và 3 thường được sử dụng cùng với thuộc tính của một hàm cơ bản là liên tục trong miền của nó. Trong trường hợp này, giải pháp đơn giản nhất và ngắn nhất cho bài toán tìm tập giá trị của hàm số theo tính chất 1, nếu có thể xác định tính đơn điệu của hàm số bằng các phương pháp đơn giản. Giải pháp của vấn đề được đơn giản hóa hơn nữa nếu hàm, ngoài ra, là chẵn hoặc lẻ, tuần hoàn, v.v. Do đó, khi giải các bài toán tìm tập giá trị của hàm, cần kiểm tra và sử dụng các thuộc tính sau của hàm khi cần thiết:

• liên tục;
• giọng bằng bằng;
• tính khác biệt;
• chẵn, lẻ, tuần hoàn, v.v.

Các tác vụ đơn giản để tìm một tập giá trị hàm chủ yếu được định hướng:

a) việc sử dụng các ước lượng và hạn chế đơn giản nhất: (2 x> 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x? 1, v.v.);

b) để chọn một hình vuông đầy đủ: x 2 - 4x + 7 \ u003d (x - 2) 2 + 3;

c) cho phép biến đổi các biểu thức lượng giác: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

d) sử dụng tính đơn điệu của hàm x 1/3 + 2 x-1 tăng R.

III. Xem xét các cách để tìm phạm vi của các hàm.

a) việc tìm kiếm tuần tự các giá trị của các đối số hàm phức;
b) phương pháp đánh giá;
c) sử dụng các tính chất của tính liên tục và tính đơn điệu của một hàm số;
d) sử dụng đạo hàm;
e) việc sử dụng các giá trị lớn nhất và nhỏ nhất của hàm;
f) phương pháp đồ thị;
g) phương pháp giới thiệu tham số;
h) phương pháp hàm ngược.

Chúng tôi sẽ tiết lộ bản chất của các phương pháp này trên các ví dụ cụ thể.

Ví dụ 1: Tìm phạm vi E (y) các hàm số y = log 0,5 (4 - 2 3 x - 9 x).

Hãy giải quyết ví dụ này bằng cách tìm tuần tự các giá trị của các đối số hàm phức. Sau khi chọn hình vuông đầy đủ theo lôgarit, chúng tôi biến đổi hàm

y = log 0,5 (5 - (1 + 2 3 x - 3 2x)) = log 0,5 (5 - (3 x + 1) 2)

Và tuần tự tìm các bộ giá trị của các đối số phức tạp của nó:

E (3 x) = (0; + ∞), E (3 x + 1) = (1; + ∞), E (- (3 x + 1) 2 = (-∞; -1), E (5 - (3 x +1) 2) = (-∞; 4)

Chứng tỏ t= 5 - (3 x +1) 2, trong đó -∞≤ t≤4. Như vậy, bài toán rút gọn là tìm tập giá trị của hàm số y = log 0,5 t trên tia (-∞;4) . Vì hàm số y = log 0,5 t chỉ xác định tại nên tập giá trị của nó trên tia (-∞; 4) trùng với tập giá trị của hàm số trên khoảng (0; 4), là giao điểm của tia (-∞; 4) với miền xác định (0; + ∞) của hàm số lôgarit. Trên khoảng (0; 4) hàm số này liên tục và giảm dần. Tại t> 0, nó có xu hướng + ∞ và khi t = 4 nhận giá trị -2, vì vậy E (y) =(-2, +∞).

Ví dụ 2: Tìm phạm vi của một hàm

y = cos7x + 5cosx

Chúng ta hãy giải quyết ví dụ này bằng phương pháp ước lượng, bản chất của nó là ước lượng hàm liên tục từ dưới lên trên và chứng minh rằng hàm đạt đến giới hạn dưới và giới hạn trên của các ước lượng. Trong trường hợp này, sự trùng hợp của tập giá trị của hàm với khoảng từ giới hạn dưới của ước lượng đến giới hạn trên được xác định bởi tính liên tục của hàm và sự vắng mặt của các giá trị khác cho nó.

Từ các bất đẳng thức -1≤cos7x? 1, -5≤5cosx? 5 ta nhận được ước lượng -6≤y? 6. Đối với x = p và x = 0, hàm nhận các giá trị -6 và 6, tức là đạt đến giới hạn dưới và giới hạn trên. Là sự kết hợp tuyến tính của các hàm liên tục cos7x và cosx, hàm y liên tục dọc theo toàn bộ trục số, do đó, theo tính chất của hàm liên tục, nó nhận tất cả các giá trị từ -6 đến 6, và chỉ chúng, vì , do bất đẳng thức -6≤y? 6, các giá trị khác cô ấy là không thể. Do đó, E (y)= [-6;6].

Ví dụ 3: Tìm phạm vi E (f) chức năng f (x)= cos2x + 2cosx.

Sử dụng công thức cosin góc kép, chúng ta biến đổi hàm f (x)= 2cos 2 x + 2cosx - 1 và ký hiệu là t= cosx. sau đó f (x)= 2t 2 + 2t - 1. Vì E (cosx) =

[-1; 1], thì phạm vi của hàm f (x) trùng với tập giá trị của hàm g (t)\ u003d 2t 2 + 2t - 1 trên đoạn [-1; 1] mà chúng ta sẽ tìm thấy bằng phương pháp đồ họa. Vẽ đồ thị của hàm số y = 2t 2 + 2t - 1 = 2 (t + 0,5) 2 - 1,5 trên khoảng [-1; 1], ta tìm được E (f) = [-1,5; 3].

Lưu ý - Nhiều bài toán về tham số được rút gọn trong việc tìm tập giá trị của hàm số, chủ yếu liên quan đến khả năng giải và số nghiệm của phương trình và bất phương trình. Ví dụ, phương trình f (x)= a có thể giải được nếu và chỉ khi

aE (f) Tương tự, phương trình f (x)= a có ít nhất một gốc nằm trên khoảng X nào đó hoặc không có gốc trên khoảng này nếu và chỉ khi a thuộc hoặc không thuộc tập giá trị của hàm f (x) trên khoảng X. Chúng ta cũng nghiên cứu sử dụng tập giá trị của hàm số và các bất phương trình f (x) ≠ một, f (x)> một v.v. Đặc biệt, f (x) ≠ và với tất cả các giá trị có thể chấp nhận của x, nếu a E (f)

Ví dụ 4. Với những giá trị nào của tham số a thì phương trình (x + 5) 1/2 = a (x 2 + 4) có một căn trên đoạn [-4; -1].

Hãy viết phương trình dưới dạng (x + 5) 1/2 / (x 2 + 4) = a. Phương trình cuối cùng có ít nhất một nghiệm nguyên trên đoạn [-4; -1] nếu và chỉ khi a thuộc tập giá trị của hàm f (x) =(x + 5) 1/2 / (x 2 + 4) trên đoạn [-4; -1]. Hãy tìm tập hợp này bằng cách sử dụng tính chất liên tục và tính đơn điệu của hàm số.

Trên đoạn [-4; -1] hàm số y = xІ + 4 liên tục, giảm dần và dương nên hàm số g (x) = 1/ (x 2 + 4) liên tục và tăng trên đoạn này, vì khi chia cho một hàm số dương, tính chất đơn điệu của hàm số chuyển thành ngược lại. Hàm số h (x) =(x + 5) 1/2 là liên tục và tăng dần trong miền của nó D (h) =[-5; + ∞) và đặc biệt, trên khoảng [-4; -1], trong đó nó cũng dương. Sau đó, hàm f (x) = g (x) h (x), là tích của hai hàm liên tục, tăng và dương, cũng liên tục và tăng trên đoạn [-4; -1], do đó tập giá trị của nó trên [-4; -1] là đoạn [ f (-4); f (-1)] =. Do đó, phương trình có nghiệm trên khoảng [-4; -1] và là nghiệm duy nhất (theo tính chất của hàm đơn điệu liên tục), với 0,05 ≤ a ≤ 0,4

Bình luận. Khả năng giải của phương trình f (x) = a trên khoảng nào đó X tương đương với việc thuộc các giá trị của tham số một tập hợp các giá trị hàm f (x) trên X. Do đó, tập giá trị của hàm f (x) trên khoảng X trùng với tập giá trị của tham số một, mà phương trình f (x) = a có ít nhất một gốc trên khoảng X. Đặc biệt, phạm vi giá trị E (f) chức năng f (x) khớp với tập hợp các giá trị tham số một, mà phương trình f (x) = a có ít nhất một gốc.

Ví dụ 5: Tìm phạm vi E (f) chức năng

Hãy giải quyết ví dụ bằng cách giới thiệu một tham số, theo đó E (f) khớp với tập hợp các giá trị tham số một, mà phương trình

có ít nhất một gốc.

Khi a = 2, phương trình là tuyến tính - 4x - 5 = 0 với hệ số khác 0 với x chưa biết, do đó nó có nghiệm. Với ≠ 2, phương trình là bậc hai, vì vậy nó có thể giải được khi và chỉ khi phân biệt của nó

Vì điểm a = 2 thuộc đoạn

thì tập hợp các giá trị tham số mong muốn một, do đó phạm vi giá trị E (f) sẽ là toàn bộ phân khúc.

Là sự phát triển trực tiếp của phương pháp đưa một tham số khi tìm tập giá trị của một hàm số, chúng ta có thể xem xét phương pháp của hàm số nghịch biến, để tìm ra phương trình cần thiết để giải phương trình cho x f (x) = y, coi y là một tham số. Nếu phương trình này có một nghiệm duy nhất x = g (y), sau đó phạm vi E (f) chức năng ban đầu f (x) trùng với miền định nghĩa D (g) chức năng trái ngược g (y). Nếu phương trình f (x) = y có nhiều giải pháp x = g 1 (y), x \ u003d g 2 (y) vv, sau đó E (f) bằng với sự kết hợp các phạm vi của các định nghĩa hàm g 1 (y), g 2 (y) vân vân.

Ví dụ 6: Tìm phạm vi E (y) các hàm số y = 5 2 / (1-3x).

Từ phương trình

tìm hàm ngược x = log 3 ((log 5 y - 2) / (log 5 y)) và miền của nó D (x):

Vì phương trình của x có nghiệm duy nhất nên

E (y) = D (x) = (0; 1) (25; + ∞).

Nếu miền của một hàm bao gồm một số khoảng hoặc hàm trên các khoảng khác nhau được cho bởi các công thức khác nhau, thì để tìm miền của hàm, bạn cần tìm các tập giá trị của hàm trên mỗi khoảng và lấy của chúng. liên hiệp.

Ví dụ 7: Tìm phạm vi f (x) và f (f (x)), ở đâu

f (x) trên tia (-∞; 1], nơi nó trùng với biểu thức 4 x + 9 4 -x + 3. Kí hiệu t = 4 x. sau đó f (x) = t + 9 / t + 3, trong đó 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f (x) trên tia (-∞; 1] trùng với tập giá trị của hàm số g (t) = t + 9 / t + 3, trên khoảng (0; 4], mà chúng tôi tìm thấy bằng cách sử dụng đạo hàm g '(t) \ u003d 1 - 9 / t 2. Trên khoảng (0; 4] đạo hàm g '(t)được xác định và biến mất ở đó lúc t = 3. Tại 0<t<3 она отрицательна, а при 3<t<4 положительна. Следовательно, в интервале (0;3) функция g (t) giảm, và trong khoảng (3; 4) nó tăng lên, liên tục trên toàn bộ khoảng (0; 4), do đó g (3)= 9 - giá trị nhỏ nhất của hàm này trên khoảng (0; 4], trong khi giá trị lớn nhất của nó không tồn tại, vì vậy khi t → 0đúng chức năng g (t) → + ∞. Sau đó, theo thuộc tính của một hàm liên tục, tập các giá trị của hàm g (t) trên khoảng (0; 4], và do đó tập giá trị f (x) trên (-∞; -1], sẽ có một tia.

Bây giờ, bằng cách kết hợp các khoảng - tập hợp các giá trị hàm f (f (x)), chứng tỏ t = f (x). sau đó f (f (x)) = f (t), ở đâu t hàm số f (t)= 2cos ( x-1) 1/2+ 7 và nó một lần nữa nhận tất cả các giá trị từ 5 đến 9, tức là phạm vi E (fІ) = E (f (f (x))) =.

Tương tự, biểu thị z = f (f (x)), bạn có thể tìm thấy phạm vi E (f3) chức năng f (f (f (x))) = f (z), trong đó 5 ≤ z ≤ 9, v.v. Đảm bảo rằng E (f 3) = .

Phương pháp phổ biến nhất để tìm tập giá trị của hàm là sử dụng các giá trị lớn nhất và nhỏ nhất của hàm trong một khoảng nhất định.

Ví dụ 8. Đối với những giá trị nào của tham số R bất đẳng thức 8 x - p ≠ 2x + 1 - 2x giữ cho tất cả -1 ≤ x< 2.

Denoting t = 2 x, chúng tôi viết bất đẳng thức dưới dạng p ≠ t 3 - 2t 2 + t. Tại vì t = 2 x là một chức năng liên tục tăng trên R, sau đó cho -1 ≤ x< 2 переменная

2 -1 ≤ t<2 2 ↔

0,5 ≤ t< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда R khác với các giá trị hàm f (t) \ u003d t 3 - 2t 2 + tở 0,5 ≤ t< 4.

Đầu tiên chúng ta hãy tìm tập giá trị của hàm f (t) trên khoảng mà nó có đạo hàm ở mọi nơi f '(t) = 3t 2 - 4t + 1. Do đó, f (t) có thể phân biệt và do đó liên tục trên phân khúc. Từ phương trình f '(t) = 0 tìm các điểm quan trọng của chức năng t = 1/3, t = 1,đầu tiên trong số đó không thuộc về phân khúc và thứ hai thuộc về nó. Tại vì f (0,5) = 1/8, f (1) = 0, f (4) = 36, sau đó, theo thuộc tính của một hàm phân biệt, 0 là giá trị nhỏ nhất và 36 là giá trị lớn nhất của hàm f (t) trên phân khúc. sau đó f (t), dưới dạng một hàm liên tục, nhận phân đoạn tất cả các giá trị từ 0 đến 36 và giá trị 36 chỉ nhận khi t = 4, vì vậy đối với 0,5 ≤ t< 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Hãy xem một bài toán trong đó cần xác định phạm vi giá trị của cung arcsine.

ví dụ 1

Tình trạng: tìm dãy y = a r c sin x.

Dung dịch

Trong trường hợp tổng quát, miền xác định của cung nằm trên khoảng [- 1; một ] . Chúng ta cần xác định giá trị lớn nhất và nhỏ nhất của hàm xác định trên đó.

y "= a r c sin x" = 1 1 - x 2

Ta biết rằng đạo hàm của hàm số sẽ dương với mọi giá trị x nằm trong khoảng [- 1; 1], nghĩa là, trong toàn bộ miền định nghĩa, hàm arcsine sẽ tăng lên. Điều này có nghĩa là nó sẽ nhận giá trị nhỏ nhất khi x bằng - 1 và lớn nhất - khi x bằng 1.

m i n x ∈ - 1; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1; 1 a r c sin x = a r c sin 1 = π 2

Do đó, khoảng của hàm arcsine sẽ bằng E (a r c sin x) = - π 2; π 2.

Câu trả lời: E (a r c sin x) \ u003d - π 2; π 2

Ví dụ 2

Tình trạng: tính khoảng y = x 4 - 5 x 3 + 6 x 2 trên đoạn [1; bốn].

Dung dịch

Tất cả những gì chúng ta cần làm là tính giá trị lớn nhất và nhỏ nhất của hàm số trong khoảng đã cho.

Để xác định điểm cực trị cần thực hiện các phép tính sau:

y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y "= 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 và l và 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1; 4 ; x3 = 15 + 338 ≈ 2,59 ∈ 1; 4

Bây giờ chúng ta hãy tìm các giá trị của hàm số đã cho tại các điểm cuối của đoạn thẳng và các điểm x 2 = 15 - 33 8; x 3 \ u003d 15 + 33 8:

y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2. 08 y 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1. 62 y (4) = 4 4 - 5 4 3 + 6 4 2 = 32

Điều này có nghĩa là tập giá trị của hàm sẽ được xác định bởi đoạn 117 - 165 33 512; 32.

Câu trả lời: 117 - 165 33 512 ; 32 .

Hãy chuyển sang việc tìm tập giá trị của hàm số liên tục y = f (x) trong các khoảng (a; b) và a; + ∞, - ∞; b, -∞; + ∞.

Hãy bắt đầu bằng cách xác định điểm lớn nhất và nhỏ nhất, cũng như khoảng thời gian tăng và giảm trong một khoảng nhất định. Sau đó, chúng ta sẽ cần tính các giới hạn một phía ở hai đầu của khoảng và / hoặc giới hạn ở vô cùng. Nói cách khác, chúng ta cần xác định hành vi của hàm trong các điều kiện đã cho. Đối với điều này, chúng tôi có tất cả các dữ liệu cần thiết.

Ví dụ 3

Tình trạng: tính đồng biến của hàm số y = 1 x 2 - 4 trên khoảng (- 2; 2).

Dung dịch

Xác định giá trị lớn nhất và nhỏ nhất của hàm số trên một khoảng cho trước

y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y "= 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2; 2)

Chúng ta nhận được giá trị lớn nhất bằng 0, vì đó là thời điểm mà dấu của hàm số thay đổi và đồ thị bắt đầu giảm. Xem hình minh họa:

Tức là y (0) = 1 0 2 - 4 = - 1 4 sẽ là giá trị lớn nhất của hàm số.

Bây giờ hãy xác định hành vi của hàm cho một x có xu hướng - 2 ở bên phải và + 2 ở bên trái. Nói cách khác, chúng tôi tìm thấy các giới hạn một phía:

lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞

Chúng tôi nhận thấy rằng các giá trị của hàm sẽ tăng từ trừ vô cùng đến - 1 4 khi đối số thay đổi từ - 2 thành 0. Và khi đối số thay đổi từ 0 thành 2, các giá trị của hàm giảm dần về phía trừ vô cùng. Do đó, tập giá trị của hàm số đã cho trên khoảng mà ta cần sẽ là (- ∞; - 1 4].

Câu trả lời: (- ∞ ; - 1 4 ] .

Ví dụ 4

Tình trạng: cho biết tập giá trị y = t g x trên khoảng đã cho - π 2; π 2.

Dung dịch

Chúng ta biết rằng, nói chung, đạo hàm của tiếp tuyến trong - π 2; π 2 sẽ là số dương, tức là, hàm sẽ tăng. Bây giờ hãy xác định cách hàm hoạt động trong các ranh giới đã cho:

lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

Chúng ta đã thu được sự gia tăng các giá trị của hàm từ trừ vô cực đến cộng vô cùng khi đối số thay đổi từ - π 2 thành π 2, và chúng ta có thể nói rằng tập nghiệm của hàm này sẽ là tập tất cả các thực. những con số.

Câu trả lời: - ∞ ; + ∞ .

Ví dụ 5

Tình trạng: xác định khoảng nào của hàm số logarit tự nhiên y = ln x.

Dung dịch

Chúng ta biết rằng hàm này được xác định cho các giá trị dương của đối số D (y) = 0; + ∞. Đạo hàm trên khoảng đã cho sẽ dương: y "= ln x" = 1 x. Điều này có nghĩa là chức năng đang tăng lên trên đó. Tiếp theo, chúng ta cần xác định giới hạn một phía cho trường hợp khi đối số chuyển sang 0 (ở phía bên phải) và khi x đi đến vô cùng:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Chúng tôi nhận thấy rằng các giá trị của hàm sẽ tăng từ trừ vô cùng đến cộng vô cùng khi giá trị x thay đổi từ 0 đến cộng vô cùng. Điều này có nghĩa là tập hợp tất cả các số thực là phạm vi của hàm lôgarit tự nhiên.

Câu trả lời: tập hợp tất cả các số thực là phạm vi của hàm lôgarit tự nhiên.

Ví dụ 6

Tình trạng: xác định khoảng nào của hàm số y = 9 x 2 + 1.

Dung dịch

Hàm này được định nghĩa với điều kiện x là một số thực. Hãy tính giá trị lớn nhất và nhỏ nhất của hàm số, cũng như khoảng thời gian tăng và giảm của nó:

y "= 9 x 2 + 1" = - 18 x (x 2 + 1) 2 y "= 0 ⇔ x = 0 y" ≤ 0 ⇔ x ≥ 0 y "≥ 0 ⇔ x ≤ 0

Kết quả là, chúng tôi đã xác định rằng hàm này sẽ giảm nếu x ≥ 0; tăng nếu x ≤ 0; nó có điểm cực đại y (0) = 9 0 2 + 1 = 9 khi biến số bằng 0.

Hãy xem hàm hoạt động như thế nào ở vô cực:

lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0

Từ bản ghi có thể thấy rằng các giá trị của hàm trong trường hợp này sẽ tiệm cận 0.

Tóm lại: khi đối số thay đổi từ trừ vô cùng thành 0, thì các giá trị của hàm sẽ tăng từ 0 đến 9. Khi các giá trị đối số đi từ 0 đến cộng với vô cùng, các giá trị hàm tương ứng sẽ giảm từ 9 xuống 0. Chúng tôi đã mô tả điều này trong hình:

Nó cho thấy rằng phạm vi của hàm sẽ là khoảng E (y) = (0; 9]

Câu trả lời: E (y) = (0; 9]

Nếu cần xác định tập giá trị của hàm số y = f (x) trên các khoảng [a; b), (a; b], [a; + ∞), (- ∞; b], thì chúng ta sẽ cần thực hiện các nghiên cứu giống hệt nhau. Chúng ta sẽ chưa phân tích các trường hợp này: chúng ta sẽ gặp chúng sau trong các bài toán .

Nhưng điều gì sẽ xảy ra nếu miền của một hàm nhất định là hợp của một số khoảng? Sau đó, chúng ta cần tính toán các bộ giá trị trên mỗi khoảng này và kết hợp chúng.

Ví dụ 7

Tình trạng: xác định khoảng của y = x x - 2.

Dung dịch

Vì mẫu số của hàm số không được chuyển thành 0 nên D (y) = - ∞; 2 ∪ 2; + ∞.

Hãy bắt đầu bằng cách xác định tập giá trị của hàm trên đoạn đầu tiên - ∞; 2, là một chùm mở. Ta biết rằng hàm số trên nó sẽ giảm, tức là đạo hàm của hàm số này sẽ âm.

lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Sau đó, trong những trường hợp đối số thay đổi theo hướng trừ đi vô cùng, các giá trị của hàm sẽ tiệm cận 1. Nếu các giá trị của x thay đổi từ trừ vô cùng thành 2, thì các giá trị sẽ giảm từ 1 xuống trừ vô cùng, tức là hàm trên đoạn này sẽ nhận các giá trị trong khoảng - ∞; một . Chúng tôi loại trừ sự thống nhất khỏi lý luận của chúng tôi, vì các giá trị của hàm không đạt đến nó, mà chỉ tiếp cận nó một cách tiệm cận.

Đối với dầm hở 2; + ∞ chúng tôi thực hiện chính xác các hành động giống nhau. Chức năng trên nó cũng đang giảm:

lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

Các giá trị của hàm trên đoạn này được xác định bởi tập 1; + ∞. Điều này có nghĩa là phạm vi giá trị của hàm được chỉ định trong điều kiện chúng ta cần sẽ là hợp của các bộ - ∞; 1 và 1; + ∞.

Câu trả lời: E (y) = - ∞; 1 ∪ 1; + ∞.

Điều này có thể được nhìn thấy trên biểu đồ:

Một trường hợp đặc biệt là các hàm tuần hoàn. Vùng giá trị của chúng trùng với tập giá trị trên khoảng tương ứng với chu kỳ của hàm này.

Ví dụ 8

Tình trạng: xác định khoảng của sin y = sin x.

Dung dịch

Sine đề cập đến một hàm tuần hoàn và chu kỳ của nó là 2 pi. Chúng tôi lấy một đoạn 0; 2 π và xem tập giá trị của nó sẽ là bao nhiêu.

y "= (sin x)" = cos x y "= 0 ⇔ cos x = 0 ⇔ x = π 2 + πk, k ∈ Z

Trong khoảng 0; 2 π thì hàm số sẽ có các điểm cực trị là π 2 và x = 3 π 2. Hãy tính xem các giá trị của hàm sẽ bằng bao nhiêu, cũng như trên các đường biên của đoạn, sau đó chúng ta chọn giá trị lớn nhất và nhỏ nhất.

y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0; 2 π sin x = sin 3 π 2 = - 1, max x ∈ 0; 2 π sinx \ u003d sin π 2 \ u003d 1

Câu trả lời: E (sinx) = - 1; một .

Nếu bạn cần biết các phạm vi của hàm số như hàm số lũy thừa, hàm số mũ, hàm số lôgarit, lượng giác nghịch đảo, thì chúng tôi khuyên bạn nên đọc lại bài viết về các hàm số sơ cấp cơ bản. Lý thuyết mà chúng tôi trình bày ở đây cho phép chúng tôi kiểm tra các giá trị được chỉ định ở đó. Bạn nên tìm hiểu chúng, vì chúng thường được yêu cầu trong việc giải quyết các vấn đề. Nếu bạn biết phạm vi của các hàm chính, thì bạn có thể dễ dàng tìm thấy phạm vi của các hàm có được từ các hàm cơ bản bằng cách sử dụng một phép biến đổi hình học.

Ví dụ 9

Tình trạng: xác định khoảng y = 3 a r c cos x 3 + 5 π 7 - 4.

Dung dịch

Chúng ta biết rằng đoạn từ 0 đến pi là khoảng của cosin nghịch đảo. Nói cách khác, E (a r c cos x) = 0; π hoặc 0 ≤ a r c cos x ≤ π. Chúng ta có thể lấy hàm a r c cos x 3 + 5 π 7 từ cung cosin bằng cách dịch chuyển và kéo dài nó dọc theo trục O x, nhưng các phép biến đổi như vậy sẽ không mang lại cho chúng ta bất cứ điều gì. Do đó, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π.

Hàm 3 a r c cos x 3 + 5 π 7 có thể nhận được từ cosin nghịch đảo a r c cos x 3 + 5 π 7 bằng cách kéo dài dọc theo trục y, tức là 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π. Phép biến đổi cuối cùng là sự dịch chuyển dọc theo trục O y theo 4 giá trị. Kết quả là, chúng ta nhận được một bất đẳng thức kép:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4

Chúng tôi nhận được rằng phạm vi chúng tôi cần sẽ bằng E (y) = - 4; 3 pi - 4.

Câu trả lời: E (y) = - 4; 3 pi - 4.

Hãy viết thêm một ví dụ mà không cần giải thích, bởi vì nó là hoàn toàn tương tự như trước đó.

Ví dụ 10

Tình trạng: tính khoảng của hàm số y = 2 2 x - 1 + 3.

Dung dịch

Hãy viết lại hàm đã cho trong điều kiện dưới dạng y = 2 · (2 ​​x - 1) - 1 2 + 3. Đối với hàm lũy thừa y = x - 1 2, khoảng xác định trên khoảng 0; + ∞, tức là x - 1 2> 0. Trong trường hợp này:

2 x - 1 - 1 2> 0 ⇒ 2 (2 x - 1) - 1 2> 0 ⇒ 2 (2 x - 1) - 1 2 + 3> 3

Vậy E (y) = 3; + ∞.

Câu trả lời: E (y) = 3; + ∞.

Bây giờ chúng ta hãy xem xét cách tìm phạm vi của một hàm không liên tục. Để làm điều này, chúng ta cần chia toàn bộ khu vực thành các khoảng và tìm các bộ giá trị trên mỗi khoảng đó, sau đó kết hợp những gì chúng ta có. Để hiểu rõ hơn về điều này, chúng tôi khuyên bạn nên xem lại các loại điểm ngắt hàm chính.

Ví dụ 11

Tình trạng:đã cho một hàm số y = 2 sin x 2 - 4, x ≤ - 3 - 1, - 3< x ≤ 3 1 x - 3 , x >3. Tính phạm vi của nó.

Dung dịch

Hàm này được xác định cho tất cả các giá trị x. Hãy phân tích nó để liên tục với các giá trị của đối số bằng - 3 và 3:

lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)

Chúng ta có một điểm gián đoạn không thể phục hồi của loại đầu tiên với giá trị của đối số - 3. Khi bạn tiếp cận nó, các giá trị của hàm có xu hướng - 2 sin 3 2 - 4, và khi x có xu hướng - 3 ở phía bên phải, các giá trị sẽ có xu hướng - 1.

lim x → 3 - 0 f (x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f (x) = lim x → 3 + 0 1 x - 3 = + ∞

Chúng ta có sự gián đoạn không thể thay đổi của loại thứ hai ở điểm 3. Khi hàm có xu hướng đến nó, các giá trị của nó tiếp cận - 1, trong khi có xu hướng đến cùng một điểm ở bên phải - đến trừ vô cùng.

Điều này có nghĩa là toàn bộ miền định nghĩa của hàm này được chia thành 3 khoảng (- ∞; - 3], (- 3; 3], (3; + ∞).

Ở phần đầu tiên, chúng tôi nhận được hàm y \ u003d 2 sin x 2 - 4. Vì - 1 ≤ sin x ≤ 1, chúng ta nhận được:

1 ≤ sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

Điều này có nghĩa là trên khoảng (- ∞; - 3] tập giá trị của hàm số là [- 6; 2].

Trên nửa khoảng (- 3; 3] ta nhận được một hàm hằng y = - 1. Do đó, toàn bộ tập giá trị của nó trong trường hợp này sẽ giảm xuống còn một số - 1.

Trên hai khoảng 3; + ∞ ta có hàm số y = 1 x - 3. Nó đang giảm vì y "= - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Do đó, tập giá trị của nguyên hàm đối với x> 3 là tập 0; + ∞. Bây giờ chúng ta hãy kết hợp các kết quả: E (y) = - 6; - 2 ∪ - 1 ∪ 0; + ∞.

Câu trả lời: E (y) = - 6; - 2 ∪ - 1 ∪ 0; + ∞.

Giải pháp được hiển thị trong đồ thị:

Ví dụ 12

Điều kiện: tồn tại hàm số y = x 2 - 3 e x. Xác định tập hợp các giá trị của nó.

Dung dịch

Nó được định nghĩa cho tất cả các giá trị đối số là số thực. Hãy để chúng tôi xác định xem hàm này sẽ tăng và giảm trong khoảng thời gian nào:

y "= x 2 - 3 e x" = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

Chúng ta biết rằng đạo hàm sẽ trở thành 0 nếu x = - 1 và x = 3. Chúng ta đặt hai điểm này trên trục và tìm xem đạo hàm sẽ có dấu hiệu gì trên các khoảng kết quả.

Hàm sẽ giảm khoảng (- ∞; - 1] ∪ [3; + ∞) và tăng thêm [- 1; 3]. Điểm tối thiểu sẽ là - 1, tối đa - 3.

Bây giờ chúng ta hãy tìm các giá trị hàm tương ứng:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

Hãy xem xét hoạt động của hàm ở vô cùng:

lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 "e x" = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x "(e x)" = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0

Để tính toán giới hạn thứ hai, quy tắc L'Hopital đã được sử dụng. Hãy vẽ giải pháp của chúng tôi trên một đồ thị.

Nó cho thấy rằng các giá trị của hàm sẽ giảm từ cộng vô cùng đến - 2 e khi đối số thay đổi từ trừ vô cùng thành - 1. Nếu nó thay đổi từ 3 thành cộng vô cùng, thì các giá trị sẽ giảm từ 6 e - 3 xuống 0, nhưng 0 sẽ không đạt được.

Như vậy, E (y) = [- 2 e; + ∞).

Câu trả lời: E (y) = [- 2 e; + ∞)

Nếu bạn nhận thấy một sai sót trong văn bản, vui lòng đánh dấu nó và nhấn Ctrl + Enter