Tangenta ku grafu funkcie v bode. Tangentová rovnica
Tangenta je priamka prechádzajúca bodom krivky a zhodujúca sa s ním v tomto bode až do prvého rádu (obr. 1).
Iná definícia: toto je limitná poloha sečnice v Δ X→0.
Vysvetlenie: Vezmite čiaru, ktorá pretína krivku v dvoch bodoch: ALE a b(pozri obrázok). Toto je sekta. Budeme ním otáčať v smere hodinových ručičiek, kým nebude mať s krivkou spoločný len jeden bod. Takže dostaneme tangens.
Presná definícia dotyčnice:
Graf dotyčnice k funkcii f, diferencovateľné v bode Xo, je priamka prechádzajúca bodom ( Xo; f(Xo)) a má sklon f′( Xo).
Svah má priamku y=kx +b. Koeficient k a je faktor sklonu túto priamku.
Uhlový koeficient sa rovná dotyčnici ostrého uhla, ktorý tvorí táto priamka s osou x:
|
Tu je uhol α uhol medzi čiarou y=kx +b a kladný (t.j. proti smeru hodinových ručičiek) smer osi x. To sa nazýva uhol sklonu rovný(Obr. 1 a 2). 
Ak je uhol sklonu rovný y=kx +b akútna, potom je sklon kladné číslo. Graf sa zväčšuje (obr. 1).
Ak je uhol sklonu rovný y=kx +b tupý, potom je sklon záporné číslo. Graf je klesajúci (obr. 2).
Ak je čiara rovnobežná s osou x, potom je sklon čiary nulový. V tomto prípade je sklon priamky tiež nulový (keďže dotyčnica nuly je nula). Rovnica s priamkou bude vyzerať ako y = b (obr. 3).
Ak je uhol sklonu priamky 90º (π/2), to znamená, že je kolmá na os x, potom je priamka daná rovnosťou x=c, kde c- nejaké reálne číslo (obr. 4).
Rovnica dotyčnice ku grafu funkcier = f(X) v bode Xo:
Príklad : Nájdite rovnicu dotyčnice ku grafu funkcie f(X) = X 3 – 2X 2 + 1 v bode s osou 2.
Riešenie .
Postupujeme podľa algoritmu.
1) Dotykový bod Xo rovná sa 2. Vypočítajte f(Xo):
f(Xo) = f(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1
2) Nájdite f′( X). Na tento účel používame vzorce diferenciácie uvedené v predchádzajúcej časti. Podľa týchto vzorcov, X 2 = 2X, a X 3 = 3X 2. znamená:
f′( X) = 3X 2 – 2 ∙ 2X = 3X 2 – 4X.
Teraz použite výslednú hodnotu f′( X), vypočítať f′( Xo):
f′( Xo) = f′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.
3) Takže máme všetky potrebné údaje: Xo = 2, f(Xo) = 1, f ′( Xo) = 4. Tieto čísla dosadíme do rovnice dotyčnice a nájdeme konečné riešenie:
y= f(Xo) + f′( Xo) (x – x o) \u003d 1 + 4 ∙ (x - 2) \u003d 1 + 4x - 8 \u003d -7 + 4x \u003d 4x - 7.
Odpoveď: y \u003d 4x - 7.
Článok poskytuje podrobné vysvetlenie definícií, geometrický význam derivátu s grafickým zápisom. Rovnicu dotyčnice budeme uvažovať na príkladoch, nájdeme rovnice dotyčnice ku krivkám 2. rádu.
Yandex.RTB R-A-339285-1 Definícia 1
Uhol sklonu priamky y \u003d k x + b sa nazýva uhol α, ktorý sa meria od kladného smeru osi x k priamke y \u003d k x + b v kladnom smere.
Na obrázku je smer ox označený zelenou šípkou a zeleným oblúkom a uhol sklonu červeným oblúkom. Modrá čiara označuje priamku.
Definícia 2
Sklon priamky y \u003d k x + b sa nazýva číselný koeficient k.
Sklon sa rovná sklonu priamky, inými slovami k = t g α .
- Sklon priamky je 0 iba vtedy, keď je o x rovnobežné a sklon sa rovná nule, pretože dotyčnica nuly je 0. Takže tvar rovnice bude y = b.
- Ak je uhol sklonu priamky y = k x + b ostrý, potom podmienky 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 a v grafe je nárast.
- Ak α \u003d π 2, potom je umiestnenie čiary kolmé na x. Rovnosť je určená rovnosťou x = c, pričom hodnota c je reálne číslo.
- Ak je uhol sklonu priamky y = k x + b tupý, potom zodpovedá podmienkam π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.
Sečna je priamka, ktorá prechádza 2 bodmi funkcie f (x). Inými slovami, sečna je priamka, ktorá prechádza cez ľubovoľné dva body na grafe danej funkcie.
Obrázok ukazuje, že A B je sečna a f (x) je čierna krivka, α je červený oblúk označujúci uhol sklonu sečny.
Keď sa sklon priamky rovná dotyčnici uhla sklonu, je zrejmé, že dotyčnicu pravouhlého trojuholníka A B C možno nájsť vo vzťahu k protiľahlej vetve k susednej vetve.
Definícia 4
Získame vzorec na nájdenie sekansu formulára:
k = t g α = B C A C = f (x B) - f x A x B - x A , kde úsečky bodov A a B sú hodnoty x A , x B a f (x A), f (x B) sú funkcie hodnôt v týchto bodoch.
Je zrejmé, že sklon sečnice je definovaný pomocou rovnosti k \u003d f (x B) - f (x A) x B - x A alebo k \u003d f (x A) - f (x B) x A - x B, pričom rovnicu treba zapísať ako y = f (x B) - f (x A) x B - x A x - x A + f (x A) resp.
y = f (x A) - f (x B) x A - x B x - x B + f (x B).
Sekanta vizuálne rozdeľuje graf na 3 časti: naľavo od bodu A, od A do B, napravo od B. Obrázok nižšie ukazuje, že existujú tri sekanty, ktoré sa považujú za rovnaké, to znamená, že sú nastaviť pomocou podobnej rovnice.
Podľa definície je jasné, že čiara a jej sečna sa v tomto prípade zhodujú.
Secant môže pretínať graf danej funkcie viackrát. Ak pre sečnicu existuje rovnica v tvare y \u003d 0, potom je počet priesečníkov so sínusoidom nekonečný.
Definícia 5
Tangenta ku grafu funkcie f (x) v bode x 0 ; f (x 0) sa nazýva priamka prechádzajúca daným bodom x 0; f (x 0) s prítomnosťou segmentu, ktorý má veľa hodnôt x blízkych x 0 .
Príklad 1
Pozrime sa bližšie na príklad nižšie. Potom je možné vidieť, že priamka daná funkciou y = x + 1 sa považuje za dotyčnicu k y = 2 x v bode so súradnicami (1 ; 2) . Pre prehľadnosť je potrebné zvážiť grafy s hodnotami blízkymi (1; 2). Funkcia y = 2 x je označená čiernou farbou, modrá čiara je dotyčnica, červená bodka je priesečník.
Je zrejmé, že y \u003d 2 x sa zlúči s čiarou y \u003d x + 1.
Na určenie dotyčnice je potrebné zvážiť správanie sa dotyčnice A B, keď sa bod B nekonečne približuje k bodu A. Kvôli prehľadnosti uvádzame obrázok.
Sečna A B označená modrou čiarou smeruje k polohe samotnej dotyčnice a uhol sklonu sečny α sa začne približovať k uhlu sklonu samotnej dotyčnice α x.
Definícia 6
Dotyčnica ku grafu funkcie y \u003d f (x) v bode A je limitná poloha sečnice A B v B smerujúcej k A, teda B → A.
Teraz prejdeme k úvahe o geometrickom význame derivácie funkcie v bode.
Prejdime k úvahe o sečnici A B pre funkciu f (x), kde A a B so súradnicami x 0, f (x 0) a x 0 + ∆ x, f (x 0 + ∆ x), a ∆ x sa označuje ako prírastok argumentu . Teraz bude mať funkcia tvar ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Pre názornosť si uveďme obrázok ako príklad.
Uvažujme výsledný pravouhlý trojuholník A B C. Na riešenie použijeme definíciu dotyčnice, to znamená, že získame pomer ∆ y ∆ x = t g α . Z definície dotyčnice vyplýva, že lim ∆ x → 0 ∆ y ∆ x = t g α x . Podľa derivačného pravidla v bode máme, že derivácia f (x) v bode x 0 sa nazýva limita pomeru prírastku funkcie k prírastku argumentu, kde ∆ x → 0, potom označujeme ako f (x 0) = lim ∆ x → 0 ∆ y ∆ x .
Z toho vyplýva, že f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, kde k x je označená ako sklon dotyčnice.
To znamená, že získame, že f ' (x) môže existovať v bode x 0 a rovnako aj dotyčnica k danému grafu funkcie v bode dotyku rovná x 0 , f 0 (x 0), kde hodnota sklonu dotyčnice v bode sa rovná derivácii v bode x 0 . Potom dostaneme, že k x = f "(x 0) .
Geometrický význam derivácie funkcie v bode je, že je daný pojem existencie dotyčnice ku grafu v tom istom bode.
Na napísanie rovnice akejkoľvek priamky v rovine je potrebné mať sklon s bodom, ktorým prechádza. Jeho označenie sa berie ako x 0 na križovatke.
Rovnica dotyčnice ku grafu funkcie y \u003d f (x) v bode x 0, f 0 (x 0) má tvar y \u003d f "(x 0) x - x 0 + f (x 0).
Znamená to, že konečná hodnota derivácie f "(x 0) môže určiť polohu dotyčnice, teda vertikálne za podmienky lim x → x 0 + 0 f" (x) = ∞ a lim x → x 0 - 0 f "(x ) = ∞ alebo neprítomnosť vôbec za podmienky lim x → x 0 + 0 f "(x) ≠ lim x → x 0 - 0 f "(x) .
Umiestnenie dotyčnice závisí od hodnoty jej sklonu k x \u003d f "(x 0). Keď je rovnobežná s osou x, dostaneme k k \u003d 0, keď je rovnobežná s približne y - k x \u003d ∞, a tvar tangentovej rovnice x \u003d x 0 rastie s k x > 0 , klesá ako k x< 0 .
Príklad 2
Zostavte rovnicu dotyčnice ku grafu funkcie y \u003d e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 v bode so súradnicami (1; 3) s definíciou uhla sklon.
Riešenie
Predpokladom je, že funkcia je definovaná pre všetky reálne čísla. Dostaneme, že bod so súradnicami určenými podmienkou (1 ; 3) je bod dotyku, potom x 0 = - 1 , f (x 0) = - 3 .
Je potrebné nájsť deriváciu v bode s hodnotou -1. Chápeme to
y "= e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = e x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = e x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Hodnota f ’ (x) v bode dotyku je sklon dotyčnice, ktorý sa rovná dotyčnici sklonu.
Potom k x = t g α x = y "(x 0) = 3 3
Z toho vyplýva, že α x = a r c t g 3 3 = π 6
odpoveď: dotyčnica má tvar
y \u003d f "(x 0) x - x 0 + f (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3
Pre názornosť uvádzame príklad v grafickom znázornení.
Čierna farba je použitá pre graf pôvodnej funkcie, modrá farba je dotyčnicový obrázok, červená bodka je dotykový bod. Obrázok vpravo ukazuje zväčšený pohľad.
Príklad 3
Zistite existenciu dotyčnice ku grafu danej funkcie
y = 3 x - 1 5 + 1 v bode so súradnicami (1 ; 1) . Napíšte rovnicu a určte uhol sklonu.
Riešenie
Predpokladom je, že definičným oborom danej funkcie je množina všetkých reálnych čísel.
Prejdime k hľadaniu derivátu
y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Ak x 0 = 1 , potom f ' (x) nie je definované, ale limity sú zapísané ako lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ a lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , čo znamená existenciu vertikálnej dotyčnice pri bod (1 ; 1) .
odpoveď: rovnica bude mať tvar x \u003d 1, kde uhol sklonu bude rovný π 2.
Pre názornosť si to nakreslíme do grafu.
Príklad 4
Nájdite body funkčného grafu y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , kde
- Tangenta neexistuje;
- Dotyčnica je rovnobežná s x;
- Dotyčnica je rovnobežná s priamkou y = 8 5 x + 4 .
Riešenie
Je potrebné venovať pozornosť oblasti definície. Predpokladom je, že funkcia je definovaná na množine všetkých reálnych čísel. Rozbaľte modul a vyriešte sústavu s intervalmi x ∈ - ∞ ; 2 a [-2; +∞). Chápeme to
y = - 115 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [ - 2; +∞)
Funkciu treba odlíšiť. To máme
y" = -115 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3, x ∈ [ - 2; +∞)
Keď x = - 2, potom derivácia neexistuje, pretože jednostranné limity nie sú v tomto bode rovnaké:
lim x → - 2 - 0 y "(x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Vypočítame hodnotu funkcie v bode x \u003d - 2, kde to dostaneme
- y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, teda dotyčnica na bod (- 2; - 2) nebude existovať.
- Dotyčnica je rovnobežná s x, keď je sklon nula. Potom k x \u003d t g α x \u003d f "(x 0). To znamená, že je potrebné nájsť hodnoty takéhoto x, keď ho derivácia funkcie zmení na nulu. Teda hodnoty f ' (x) a budú to dotykové body, kde dotyčnica je rovnobežná s x .
Keď x ∈ - ∞ ; - 2 , potom - 1 5 (x 2 + 12 x + 35) = 0 a pre x ∈ (- 2; + ∞) dostaneme 1 5 (x 2 - 4 x + 3) = 0 .
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2; +∞
Vypočítame zodpovedajúce hodnoty funkcie
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 r 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Preto - 5; 85,-4; 4 3, 1; 85, 3; 4 3 sa považujú za požadované body grafu funkcie.
Zvážte grafické znázornenie riešenia.
Čierna čiara je graf funkcie, červené bodky sú dotykové body.
- Keď sú čiary rovnobežné, sklony sú rovnaké. Potom je potrebné hľadať body grafu funkcie, kde sa sklon bude rovnať hodnote 8 5 . Aby ste to urobili, musíte vyriešiť rovnicu v tvare y "(x) = 8 5. Potom, ak x ∈ - ∞; - 2, dostaneme, že - 1 5 (x 2 + 12 x + 35) = 8 5, a ak x ∈ ( - 2; + ∞), potom 1 5 (x 2 - 4 x + 3) = 85.
Prvá rovnica nemá korene, pretože diskriminant je menší ako nula. Poďme si to zapísať
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Ďalšia rovnica má teda dva skutočné korene
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2; +∞
Prejdime k hľadaniu hodnôt funkcie. Chápeme to
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Body s hodnotami - 1; 4 15, 5; 8 3 sú body, kde dotyčnice sú rovnobežné s priamkou y = 8 5 x + 4 .
odpoveď:čierna čiara - graf funkcie, červená čiara - graf y \u003d 8 5 x + 4, modrá čiara - dotyčnice v bodoch - 1; 4 15, 5; 8 3.
Existencia nekonečného počtu dotyčníc pre dané funkcie je možná.
Príklad 5
Napíšte rovnice všetkých dostupných dotyčníc funkcie y = 3 cos 3 2 x - π 4 - 1 3 , ktoré sú kolmé na priamku y = - 2 x + 1 2 .
Riešenie
Na zostavenie tangentovej rovnice je potrebné nájsť koeficient a súradnice bodu dotyku na základe podmienky kolmosti čiar. Definícia znie takto: súčin svahov, ktoré sú kolmé na priamky, sa rovná - 1, to znamená, že je napísaný ako k x · k ⊥ = - 1. Z podmienky máme, že sklon je kolmý na priamku a rovná sa k ⊥ = - 2, potom k x = - 1 k ⊥ = - 1 - 2 = 1 2 .
Teraz musíme nájsť súradnice dotykových bodov. Musíte nájsť x, po ktorom je jeho hodnota pre danú funkciu. Všimnite si, že z geometrického významu derivácie v bode
x 0 dostaneme, že k x \u003d y "(x 0) . Z tejto rovnosti nájdeme hodnoty x pre dotykové body.
Chápeme to
y "(x 0) = 3 cos 3 2 x 0 - π 4 - 1 3" = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 \u003d - 9 2 sin 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 sin 3 2 x 0 - π 4 \u003d 1 2 ⇒ x sin 3 π 4 = - 19
Táto trigonometrická rovnica sa použije na výpočet súradníc bodov dotyku.
3 2 x 0 - π 4 = a rc sin - 1 9 + 2 πk alebo 3 2 x 0 - π 4 = π - a rc sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a rc sin 1 9 + 2 πk alebo 3 2 x 0 - π 4 = π + a rc sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a rc sin 1 9 + 2 πk alebo x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z je množina celých čísel.
Našlo sa x styčných bodov. Teraz musíte prejsť na vyhľadávanie hodnôt y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - hriech 2 3 2 x 0 - π 4 - 1 3 alebo y 0 = 3 - 1 - hriech 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 alebo y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 alebo y 0 = - 4 5 + 1 3
Odtiaľto dostaneme, že 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3, 2 3 5 π 4 + a rc sin 1 9 + 2 πk; - 4 5 + 1 3 sú dotykové body.
odpoveď: potrebné rovnice budú napísané ako
y = 1 2 x - 2 3 π 4 - a rc sin 1 9 + 2 πk + 4 5 - 1 3, y = 1 2 x - 2 3 5 π 4 + a rc sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
Pre vizuálnu reprezentáciu zvážte funkciu a dotyčnicu na súradnicovej čiare.
Obrázok ukazuje, že umiestnenie funkcie je na intervale [-10; 10 ] , kde čierna čiara je grafom funkcie, modré čiary sú dotyčnice, ktoré sú kolmé na danú priamku tvaru y = - 2 x + 1 2 . Červené bodky sú dotykové body.
Kanonické rovnice kriviek 2. rádu nie sú jednohodnotové funkcie. Tangentové rovnice pre nich sú zostavené podľa známych schém.
Tangenta ku kruhu
Ak chcete nastaviť kruh so stredom v bode x c e n t e r ; y c e n t e r a polomer R, použije sa vzorec x - x c e n t e r 2 + y - y c e n t e r 2 = R2.
Túto rovnosť možno zapísať ako spojenie dvoch funkcií:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Prvá funkcia je hore a druhá dole, ako je znázornené na obrázku.
Zostaviť rovnicu kružnice v bode x 0 ; y 0 , ktorý sa nachádza v hornom alebo dolnom polkruhu, mali by ste nájsť rovnicu funkčného grafu tvaru y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r alebo y \u003d - R 2 - x - x c e r 2 y c e n t e r v určenom bode.
Keď v bodoch x c e n t e r ; y c e n t e r + R a x c e n t e r; y c e n t e r - R dotyčnice môžu byť dané rovnicami y = y c e n t e r + R a y = y c e n t e r - R a v bodoch x c e n t e r + R; y c e n t e r a
x c e n t e r - R; y c e n t e r bude rovnobežné s y, potom dostaneme rovnice tvaru x = x c e n t e r + R a x = x c e n t e r - R .
Tangenta k elipse
Keď je elipsa vycentrovaná v x c e n t e r ; y c e n t e r s poloosami a a b , potom ho možno zadať pomocou rovnice x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .
Elipsu a kruh možno označiť kombináciou dvoch funkcií, a to hornej a dolnej polelipsy. Potom to dostaneme
y = b a a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a a 2 - (x - x c e n t e r) 2 + y c e n t e r
Ak sú dotyčnice umiestnené vo vrcholoch elipsy, potom sú rovnobežné okolo x alebo okolo y. Pre prehľadnosť zvážte obrázok nižšie.
Príklad 6
Napíšte rovnicu dotyčnice k elipse x - 3 2 4 + y - 5 2 25 = 1 v bodoch s hodnotami x rovnými x = 2 .
Riešenie
Je potrebné nájsť dotykové body, ktoré zodpovedajú hodnote x = 2. Urobíme substitúciu do existujúcej rovnice elipsy a získame ju
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Potom 2; 5 3 2 + 5 a 2; - 5 3 2 + 5 sú dotykové body, ktoré patria hornej a dolnej polelipse.
Prejdime k hľadaniu a riešeniu rovnice elipsy vzhľadom na y. Chápeme to
x - 3 2 4 + y - 5 2 25 = 1 r - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Je zrejmé, že horná polelipsa je špecifikovaná pomocou funkcie tvaru y = 5 + 5 2 4 - x - 3 2 a dolná y = 5 - 5 2 4 - x - 3 2 .
Použijeme štandardný algoritmus, aby sme sformulovali rovnicu dotyčnice ku grafu funkcie v bode. Píšeme, že rovnica pre prvú dotyčnicu v bode 2 ; 5 3 2 + 5 bude vyzerať
y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Dostaneme, že rovnica druhej dotyčnice s hodnotou v bode
2; - 5 3 2 + 5 sa stáva
y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Graficky sú dotyčnice označené takto:
Tangenta k hyperbole
Keď má hyperbola stred v bode x c e n t e r ; y c e n t e r a vrcholy x c e n t e r + α ; y c e n t e r a x c e n t e r - a; y c e n t e r , je daná nerovnosť x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 , ak s vrcholmi x c e n t e r ; y c e n t e r + b a x c e n t e r; y c e n t e r - b je potom dané nerovnicou x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = -1 .
Hyperbola môže byť reprezentovaná ako dve kombinované funkcie formulára
y = b a (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a (x - x c e n t e r) 2 - a 2 + y c e r alebo y = b a (x - x c - e) ) 2 + a 2 + y c e n t e r
V prvom prípade platí, že dotyčnice sú rovnobežné s y a v druhom sú rovnobežné s x.
Z toho vyplýva, že na nájdenie rovnice dotyčnice k hyperbole je potrebné zistiť, do ktorej funkcie dotyčnicový bod patrí. Aby sme to určili, je potrebné vykonať substitúciu v rovniciach a skontrolovať ich identitu.
Príklad 7
Napíšte rovnicu dotyčnice k hyperbole x - 3 2 4 - y + 3 2 9 = 1 v bode 7; - 3 3 - 3 .
Riešenie
Záznam riešenia nájdenia hyperboly je potrebné transformovať pomocou 2 funkcií. Chápeme to
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 alebo y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Je potrebné zistiť, do ktorej funkcie daný bod so súradnicami 7 patrí; - 3 3 - 3 .
Je zrejmé, že na kontrolu prvej funkcie potrebujete y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , potom bod nepatrí do grafu, pretože nie je splnená rovnosť.
Pre druhú funkciu platí, že y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , čo znamená, že bod patrí do daného grafu. Odtiaľ by ste mali nájsť koeficient sklonu.
Chápeme to
y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
odpoveď: tangensová rovnica môže byť reprezentovaná ako
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Je vizualizovaný nasledovne:
Tangenta k parabole
Na zostavenie rovnice dotyčnice k parabole y \u003d a x 2 + b x + c v bode x 0, y (x 0) , musíte použiť štandardný algoritmus, potom bude mať rovnica tvar y \u003d y " (x 0) x - x 0 + y ( x 0) Takáto dotyčnica vo vrchole je rovnobežná s x.
Parabola x = a y 2 + b y + c by mala byť definovaná ako spojenie dvoch funkcií. Preto musíme vyriešiť rovnicu pre y. Chápeme to
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Znázornime to ako:
Ak chcete zistiť, či bod x 0 , y (x 0) patrí funkcii, jemne postupujte podľa štandardného algoritmu. Takáto dotyčnica bude rovnobežná s y vzhľadom na parabolu.
Príklad 8
Napíšte rovnicu dotyčnice ku grafu x - 2 y 2 - 5 y + 3, keď máme sklon dotyčnice 150°.
Riešenie
Riešenie začneme reprezentáciou paraboly ako dvoch funkcií. Chápeme to
2 r 2 - 5 r + 3 - x = 0 D = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 r = 5 - 49 - 8 x - 4
Hodnota sklonu sa rovná hodnote derivácie v bode x 0 tejto funkcie a rovná sa dotyčnici sklonu.
Dostaneme:
k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3
Odtiaľ určíme hodnotu x pre dotykové body.
Prvá funkcia bude napísaná ako
y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Je zrejmé, že neexistujú žiadne skutočné korene, pretože sme dostali zápornú hodnotu. Dospeli sme k záveru, že pre takúto funkciu neexistuje dotyčnica s uhlom 150 °.
Druhá funkcia bude napísaná ako
y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Máme, že dotykové body - 23 4 ; - 5 + 3 4 .
odpoveď: dotyčnica má tvar
y = - 1 3 x - 23 4 + - 5 + 3 4
Znázornime to takto:
Ak si všimnete chybu v texte, zvýraznite ju a stlačte Ctrl+Enter
Rovnica dotyčnice ku grafu funkcie
P. Romanov, T. Romanova,
Magnitogorsk,
Čeľabinská oblasť
Rovnica dotyčnice ku grafu funkcie
Článok vyšiel s podporou Hotelového komplexu ITAKA+. Pri pobyte v meste staviteľov lodí Severodvinsk nebudete čeliť problému nájsť dočasné bývanie. , na webovej stránke hotelového komplexu "ITAKA +" http://itakaplus.ru si môžete jednoducho a rýchlo prenajať byt v meste na akékoľvek obdobie s dennou platbou.
V súčasnej etape rozvoja vzdelávania je jednou z jeho hlavných úloh formovanie tvorivo mysliacej osobnosti. Schopnosť tvorivosti u žiakov možno rozvíjať len vtedy, ak sa systematicky zapájajú do základov výskumnej činnosti. Základom pre uplatnenie tvorivých síl, schopností a talentu študentov sú plnohodnotné vedomosti a zručnosti. V tomto smere je nemenej dôležitý problém vytvorenia systému základných vedomostí a zručností pre každú tému školského kurzu matematiky. Plnohodnotné zručnosti by zároveň mali byť didaktickým cieľom nie jednotlivých úloh, ale ich dôkladne premysleného systému. V najširšom zmysle je systém chápaný ako súbor vzájomne prepojených prvkov, ktoré majú integritu a stabilnú štruktúru.
Zvážte metodológiu na výučbu študentov, ako zostaviť rovnicu dotyčnice ku grafu funkcie. V podstate sú všetky úlohy na nájdenie dotyčnicovej rovnice redukované na potrebu vybrať z množiny (zväzku, rodiny) čiar tie z nich, ktoré spĺňajú určitú požiadavku - sú dotyčnicami ku grafu určitej funkcie. V tomto prípade je možné množinu riadkov, z ktorých sa vykonáva výber, určiť dvoma spôsobmi:
a) bod ležiaci v rovine xOy (stredová ceruzka čiar);
b) uhlový koeficient (paralelný zväzok priamok).
V tomto ohľade sme pri štúdiu témy „Dotyčnosť ku grafu funkcie“ s cieľom izolovať prvky systému identifikovali dva typy úloh:
1) úlohy na dotyčnici danej bodom, ktorým prechádza;
2) úlohy na dotyčnici danej jej sklonom.
Učenie sa riešiť problémy na dotyčnici sa uskutočnilo pomocou algoritmu navrhnutého A.G. Mordkovič. Jeho zásadný rozdiel od už známych je v tom, že úsečka dotykového bodu sa označuje písmenom a (namiesto x0), v súvislosti s ktorým má dotyčnica tvar
y \u003d f (a) + f "(a) (x - a)
(porovnaj s y \u003d f (x 0) + f "(x 0) (x - x 0)). Táto metodická technika podľa nášho názoru umožňuje študentom rýchlo a jednoducho si uvedomiť, kde sú zapísané súradnice aktuálneho bodu vo všeobecnej tangentovej rovnici a kde sú body dotyku.
Algoritmus na zostavenie rovnice dotyčnice ku grafu funkcie y = f(x)
1. Označte písmenom a úsečku bodu kontaktu.
2. Nájdite f(a).
3. Nájdite f "(x) a f "(a).
4. Do všeobecnej rovnice dotyčnice y \u003d f (a) \u003d f "(a) (x - a) dosaďte nájdené čísla a, f (a), f "(a).
Tento algoritmus je možné zostaviť na základe nezávislého výberu operácií študentmi a postupnosti ich vykonávania.
Prax ukázala, že dôsledné riešenie každej z kľúčových úloh pomocou algoritmu vám umožňuje vytvoriť schopnosť písať rovnicu dotyčnice ku grafu funkcie v etapách a kroky algoritmu slúžia ako silné body pre akcie. . Tento prístup zodpovedá teórii postupného formovania mentálnych akcií, ktorú vyvinul P.Ya. Galperin a N.F. Talyzina.
V prvom type úloh boli identifikované dve kľúčové úlohy:
- dotyčnica prechádza bodom ležiacim na krivke (úloha 1);
- dotyčnica prechádza bodom, ktorý neleží na krivke (úloha 2).
Úloha 1. Prirovnajte dotyčnicu ku grafu funkcie 
v bode M(3; – 2).
Riešenie. Bod M(3; – 2) je bod dotyku, pretože
1. a = 3 - úsečka bodu dotyku.
2. f(3) = – 2.
3. f "(x) \u003d x 2 - 4, f "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 je rovnica dotyčnice.
Úloha 2. Napíšte rovnice všetkých dotyčníc ku grafu funkcie y = - x 2 - 4x + 2, prechádzajúceho bodom M(- 3; 6).
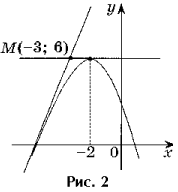Riešenie. Bod M(– 3; 6) nie je dotykový bod, pretože f(– 3) 6 (obr. 2).
2. f(a) = – a 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - rovnica dotyčnice.
Dotyčnica prechádza bodom M(– 3; 6), preto jej súradnice vyhovujú rovnici dotyčnice.
6 = – a 2 – 4a + 2 – 2 (a + 2) (– 3 – a),
a 2 + 6a + 8 = 0^ a 1 = - 4, a 2 = - 2.
Ak a = – 4, potom rovnica dotyčnice je y = 4x + 18.
Ak a \u003d - 2, potom rovnica dotyčnice má tvar y \u003d 6.
V druhom type budú kľúčové úlohy nasledovné:
- dotyčnica je rovnobežná s nejakou priamkou (úloha 3);
- dotyčnica prechádza pod určitým uhlom k danej priamke (úloha 4).
Úloha 3. Napíšte rovnice všetkých dotyčníc ku grafu funkcie y \u003d x 3 - 3x 2 + 3 rovnobežne s priamkou y \u003d 9x + 1.
Riešenie.
1. a - úsečka bodu dotyku.
2. f(a) = a 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.
Ale na druhej strane, f "(a) \u003d 9 (podmienka paralelnosti). Musíme teda vyriešiť rovnicu 3a 2 - 6a \u003d 9. Jej korene a \u003d - 1, a \u003d 3 (obr. 3).
4. 1) a = – 1;
2) f(– 1) = – 1;
3) f" (– 1) = 9;
4) y = – 1 + 9 (x + 1);
y = 9x + 8 je rovnica dotyčnice;
1) a = 3;
2) f(3) = 3;
3) f"(3) = 9;
4) y = 3 + 9 (x - 3);
y = 9x – 24 je rovnica dotyčnice.
Úloha 4. Napíšte rovnicu dotyčnice ku grafu funkcie y = 0,5x 2 - 3x + 1, prechádzajúcej pod uhlom 45° k priamke y = 0 (obr. 4).
Riešenie. Z podmienky f "(a) \u003d tg 45 ° nájdeme a: a - 3 \u003d 1^a=4.
1. a = 4 - úsečka bodu dotyku.
2. f(4) = 8 - 12 + 1 = - 3.
3. f "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).
y \u003d x - 7 - rovnica dotyčnice.
Je ľahké ukázať, že riešenie akéhokoľvek iného problému sa redukuje na riešenie jedného alebo niekoľkých kľúčových problémov. Zvážte nasledujúce dva problémy ako príklad.
1. Napíšte rovnice dotyčníc k parabole y = 2x 2 - 5x - 2, ak sa dotyčnice pretínajú v pravom uhle a jedna z nich sa dotýka paraboly v bode s osou 3 (obr. 5).
Riešenie. Keďže je daná úsečka bodu kontaktu, prvá časť riešenia je zredukovaná na kľúčový problém 1.
1. a \u003d 3 - súradnica bodu dotyku jednej zo strán pravého uhla.
2. f(3) = 1.
3. f "(x) \u003d 4x - 5, f "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - rovnica prvej dotyčnice.
Nechajte a je uhol sklonu prvej dotyčnice. Pretože dotyčnice sú kolmé, potom je uhol sklonu druhej dotyčnice. Z rovnice y = 7x – 20 prvej dotyčnice máme tg a = 7. Nájdite
To znamená, že sklon druhej dotyčnice je .
Ďalšie riešenie je zredukované na kľúčovú úlohu 3.
Nech B(c; f(c)) je dotykový bod druhej priamky
1. - úsečka druhého styčného bodu.
2.
3.
4.je rovnica druhej dotyčnice.
Poznámka. Uhlový koeficient dotyčnice ľahšie zistíme, ak žiaci poznajú pomer koeficientov kolmých priamok k 1 k 2 = - 1.
2. Napíšte rovnice všetkých spoločných dotyčníc k funkčným grafom
Riešenie. Úloha sa redukuje na nájdenie úsečiek styčných bodov spoločných dotyčníc, teda na riešenie kľúčovej úlohy 1 vo všeobecnom tvare, zostavenie sústavy rovníc a jej následné riešenie (obr. 6).
1. Nech a je úsečka bodu dotyku ležiaceho na grafe funkcie y = x 2 + x + 1.
2. f(a) = a 2 + a + 1.
3. f "(a) = 2a + 1.
4. y \u003d a 2 + a + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - a 2.
1. Nech c je úsečka dotykového bodu ležiaceho na grafe funkcie
2.
3. f "(c) = c.
4.
Keďže dotyčnice sú spoločné, teda
Takže y = x + 1 a y = - 3x - 3 sú spoločné dotyčnice.
Hlavným cieľom uvažovaných úloh je pripraviť študentov na sebapoznanie typu kľúčovej úlohy pri riešení zložitejších úloh, ktoré si vyžadujú určité výskumné zručnosti (schopnosť analyzovať, porovnávať, zovšeobecňovať, predkladať hypotézy atď.). Takéto úlohy zahŕňajú akúkoľvek úlohu, v ktorej je kľúčová úloha zahrnutá ako komponent. Uvažujme ako príklad problém (inverzný k problému 1) nájsť funkciu z rodiny jej dotyčníc.
3. Pre čo b a c sú priamky y \u003d x a y \u003d - 2x dotyčnica ku grafu funkcie y \u003d x 2 + bx + c?
Riešenie.
Nech t je úsečka bodu dotyku priamky y = x s parabolou y = x 2 + bx + c; p je úsečka bodu dotyku priamky y = - 2x s parabolou y = x 2 + bx + c. Potom rovnica dotyčnice y = x bude mať tvar y = (2t + b)x + c - t 2 a rovnica dotyčnice y = - 2x bude mať tvar y = (2p + b)x + c - p 2 .
Zostavte a vyriešte sústavu rovníc
odpoveď: 
Úlohy na samostatné riešenie
1. Napíšte rovnice dotyčníc nakreslených ku grafu funkcie y = 2x 2 - 4x + 3 v priesečníkoch grafu s priamkou y = x + 3.
Odpoveď: y \u003d - 4x + 3, y \u003d 6x - 9,5.
2. Pre aké hodnoty a prechádza dotyčnica nakreslená ku grafu funkcie y \u003d x 2 - os v bode grafu s os x 0 \u003d 1 cez bod M (2; 3) ?
Odpoveď: a = 0,5.
3. Pre aké hodnoty p sa priamka y = px - 5 dotýka krivky y = 3x 2 - 4x - 2?
Odpoveď: p 1 \u003d - 10, p 2 \u003d 2.
4. Nájdite všetky spoločné body grafu funkcie y = 3x - x 3 a dotyčnicu nakreslenú k tomuto grafu cez bod P(0; 16).
Odpoveď: A(2; - 2), B (- 4; 52).
5. Nájdite najkratšiu vzdialenosť medzi parabolou y = x 2 + 6x + 10 a priamkou
odpoveď:
6. Na krivke y \u003d x 2 - x + 1 nájdite bod, v ktorom je dotyčnica ku grafu rovnobežná s priamkou y - 3x + 1 \u003d 0.
Odpoveď: M(2; 3).
7. Napíšte rovnicu dotyčnice ku grafu funkcie y = x 2 + 2x - | 4x | ktorý sa ho dotýka v dvoch bodoch. Urobte si kresbu.
Odpoveď: y = 2x - 4.
8. Dokážte, že priamka y = 2x – 1 nepretína krivku y = x 4 + 3x 2 + 2x. Nájdite vzdialenosť medzi ich najbližšími bodmi.
odpoveď:
9. Na parabole y \u003d x 2 sa zoberú dva body s úsečkami x 1 \u003d 1, x 2 \u003d 3. Cez tieto body sa nakreslí sečna. V ktorom bode paraboly bude dotyčnica k nej rovnobežná s nakreslenou sečnicou? Napíšte rovnice pre sečnicu a dotyčnicu.
Odpoveď: y \u003d 4x - 3 - rovnica sečny; y = 4x – 4 je rovnica dotyčnice.
10. Nájdite uhol q medzi dotyčnicami ku grafu funkcie y \u003d x 3 - 4x 2 + 3x + 1, nakreslených v bodoch s os 0 a 1.
Odpoveď: q = 45°.
11. V ktorých bodoch zviera dotyčnica ku grafu funkcie s osou Ox uhol 135°?
Odpoveď: A(0; - 1), B(4; 3).
12. V bode A(1; 8) ku krivke 
nakreslí sa dotyčnica. Nájdite dĺžku dotyčnicového segmentu uzavretého medzi súradnicovými osami.
odpoveď:
13. Napíšte rovnicu všetkých spoločných dotyčníc ku grafom funkcií y \u003d x 2 - x + 1 a y \u003d 2x 2 - x + 0,5.
Odpoveď: y = - 3x a y = x.
14. Nájdite vzdialenosť medzi dotyčnicami ku grafu funkcie 
rovnobežne s osou x.
odpoveď:
15. Určte, pod akými uhlami parabola y \u003d x 2 + 2x - 8 pretína os x.
Odpoveď: q 1 \u003d arctan 6, q 2 \u003d arctan (- 6).
16. Na grafe funkcie 
nájdite všetky body, z ktorých dotyčnica k tomuto grafu pretína kladné poloosi súradníc a oddeľuje od nich rovnaké segmenty.
Odpoveď: A(-3; 11).
17. Priamka y = 2x + 7 a parabola y = x 2 – 1 sa pretínajú v bodoch M a N. Nájdite priesečník K priamok dotýkajúcich sa paraboly v bodoch M a N.
Odpoveď: K(1; - 9).
18. Pre aké hodnoty b je priamka y \u003d 9x + b dotyčnica ku grafu funkcie y \u003d x 3 - 3x + 15?
Odpoveď: - 1; 31.
19. Pre aké hodnoty k má priamka y = kx – 10 iba jeden spoločný bod s grafom funkcie y = 2x 2 + 3x – 2? Pre nájdené hodnoty k určite súradnice bodu.
Odpoveď: k1 = - 5, A(- 2; 0); k2 = 11, B(2; 12).
20. Pre aké hodnoty b prechádza dotyčnica nakreslená ku grafu funkcie y = bx 3 – 2x 2 – 4 v bode s os x 0 = 2 bodom M(1; 8)?
Odpoveď: b = - 3.
21. Parabola s vrcholom na osi x je dotyčnicou priamky prechádzajúcej bodmi A(1; 2) a B(2; 4) v bode B. Nájdite rovnicu paraboly.
odpoveď: 
22. Pri akej hodnote koeficientu k sa parabola y \u003d x 2 + kx + 1 dotýka osi Ox?
Odpoveď: k = q 2.
23. Nájdite uhly medzi priamkou y = x + 2 a krivkou y = 2x 2 + 4x - 3.
29. Nájdite vzdialenosť medzi dotyčnicami ku grafu generátorov funkcií s kladným smerom osi Ox pod uhlom 45°.
odpoveď:
30. Nájdite ťažisko vrcholov všetkých parabol v tvare y = x 2 + ax + b dotýkajúcich sa priamky y = 4x - 1.
Odpoveď: priamka y = 4x + 3.
Literatúra
1. Zvavich L.I., Shlyapochnik L.Ya., Chinkina M.V. Algebra a začiatky analýzy: 3600 problémov pre školákov a uchádzačov o univerzitu. - M., Drop, 1999.
2. Mordkovich A. Štvrtý seminár pre mladých učiteľov. Témou je „Aplikácie odvodených“. - M., "Matematika", č. 21/94.
3. Formovanie vedomostí a zručností na základe teórie postupnej asimilácie mentálnych akcií. / Ed. P.Ya. Galperin, N.F. Talyzina. - M., Moskovská štátna univerzita, 1968.
Tangenta je priamka , ktorý sa v jednom bode dotýka grafu funkcie a ktorého všetky body sú v najmenšej vzdialenosti od grafu funkcie. Preto dotyčnica prechádza dotyčnicou ku grafu funkcie pod určitým uhlom a niekoľko dotyčníc nemôže prechádzať bodom dotyčnice pod rôznymi uhlami. Dotyčnicové rovnice a rovnice normály ku grafu funkcie sú zostavené pomocou derivácie.
Rovnica dotyčnice je odvodená z rovnice priamky .
Odvodíme rovnicu dotyčnice a potom rovnicu normály ku grafu funkcie.
r = kx + b .
V ňom k- uhlový koeficient.
Odtiaľ dostaneme nasledujúci záznam:
r - r 0 = k(X - X 0 ) .
Hodnota derivátu f "(X 0 ) funkcie r = f(X) v bode X0 rovná sklonu k=tg φ dotyčnica ku grafu funkcie nakreslenej cez bod M0 (X 0 , r 0 ) , kde r0 = f(X 0 ) . To je čo geometrický význam derivátu .
Môžeme teda nahradiť k na f "(X 0 ) a získajte nasledujúce rovnica dotyčnice ku grafu funkcie :
r - r 0 = f "(X 0 )(X - X 0 ) .
V úlohách na zostavenie rovnice dotyčnice ku grafu funkcie (a čoskoro k nim prejdeme) je potrebné uviesť rovnicu získanú z vyššie uvedeného vzorca do všeobecná rovnica priamky. Aby ste to dosiahli, musíte preniesť všetky písmená a čísla na ľavú stranu rovnice a na pravej strane nechať nulu.
Teraz o normálnej rovnici. Normálne je priamka prechádzajúca bodom dotyčnice ku grafu funkcie kolmá na dotyčnicu. Normálna rovnica :
(X - X 0 ) + f "(X 0 )(r - r 0 ) = 0
Ak chcete zahriať prvý príklad, musíte ho vyriešiť sami a potom sa pozrieť na riešenie. Je dôvod dúfať, že táto úloha nebude pre našich čitateľov „studenou sprchou“.
Príklad 0. Zostavte rovnicu dotyčnice a rovnicu normály ku grafu funkcie v bode M (1, 1) .
Príklad 1 Zostavte rovnicu dotyčnice a rovnicu normály ku grafu funkcie 
ak úsečka bodu dotyku je .
Poďme nájsť deriváciu funkcie:
Teraz máme všetko, čo je potrebné dosadiť do položky uvedenej v teoretickej referencii, aby sme získali tangentovú rovnicu. Dostaneme
V tomto príklade sme mali šťastie: sklon sa ukázal byť rovný nule, takže nebolo potrebné samostatne uviesť rovnicu do všeobecného tvaru. Teraz môžeme napísať normálnu rovnicu:
Na obrázku nižšie: graf funkcie v bordovej farbe, dotyčnica v zelenej, normála v oranžovej.
Nasledujúci príklad tiež nie je zložitý: funkcia, ako v predchádzajúcom, je tiež polynóm, ale koeficient sklonu sa nebude rovnať nule, takže sa pridá ešte jeden krok - uvedenie rovnice do všeobecného tvaru.
Príklad 2
Riešenie. Poďme nájsť ordinátu bodu dotyku:
Poďme nájsť deriváciu funkcie:
.
Nájdite hodnotu derivácie v bode dotyku, teda sklon dotyčnice:
Všetky získané údaje dosadíme do „prázdneho vzorca“ a dostaneme tangentovú rovnicu:
Privedieme rovnicu do všeobecného tvaru (zhromažďujeme všetky písmená a čísla iné ako nula na ľavej strane a nulu necháme na pravej strane):
Zostavíme rovnicu normály:
Príklad 3 Zostavte rovnicu dotyčnice a rovnicu normály ku grafu funkcie, ak úsečka bodu dotyku je .
Riešenie. Poďme nájsť ordinátu bodu dotyku:
Poďme nájsť deriváciu funkcie:
.
Nájdite hodnotu derivácie v bode dotyku, teda sklon dotyčnice:
.
Nájdeme rovnicu dotyčnice:
Pred uvedením rovnice do všeobecného tvaru ju musíte trochu „skombinovať“: vynásobte člen po člene 4. Urobíme to a rovnicu uvedieme do všeobecného tvaru:
Zostavíme rovnicu normály:
Príklad 4 Zostavte rovnicu dotyčnice a rovnicu normály ku grafu funkcie, ak úsečka bodu dotyku je .
Riešenie. Poďme nájsť ordinátu bodu dotyku:
.
Poďme nájsť deriváciu funkcie:
Nájdite hodnotu derivácie v bode dotyku, teda sklon dotyčnice:
.
Dostaneme tangentovú rovnicu:
Prinášame rovnicu do všeobecného tvaru:
Zostavíme rovnicu normály:
Častou chybou pri písaní tangensových a normálnych rovníc je nevšimnúť si, že funkcia uvedená v príklade je zložitá a vypočítať jej deriváciu ako deriváciu jednoduchej funkcie. Nasledujúce príklady už sú komplexné funkcie(príslušná lekcia sa otvorí v novom okne).
Príklad 5 Zostavte rovnicu dotyčnice a rovnicu normály ku grafu funkcie, ak úsečka bodu dotyku je .
Riešenie. Poďme nájsť ordinátu bodu dotyku:
Pozor! Táto funkcia je zložitá, pretože argument dotyčnice (2 X) je sama osebe funkciou. Preto deriváciu funkcie nájdeme ako deriváciu komplexnej funkcie.
Inštrukcia
V bode M určíme sklon dotyčnice ku krivke.
Krivka predstavujúca graf funkcie y = f(x) je súvislá v niektorom okolí bodu M (vrátane samotného bodu M).
Ak hodnota f‘(x0) neexistuje, potom buď neexistuje dotyčnica, alebo prechádza vertikálne. Z tohto hľadiska je prítomnosť derivácie funkcie v bode x0 spôsobená existenciou nevertikálnej dotyčnice, ktorá je v kontakte s grafom funkcie v bode (x0, f(x0)). V tomto prípade sa sklon dotyčnice bude rovnať f "(x0). Tým sa objasní geometrický význam derivácie - výpočet sklonu dotyčnice.
Nájdite hodnotu úsečky bodu dotyku, ktorý je označený písmenom „a“. Ak sa zhoduje s daným dotykovým bodom, potom „a“ bude jeho x-ová súradnica. Určte hodnotu funkcie f(a), dosadzovanie do rovnice funkcie veľkosť úsečky.
Určte prvú deriváciu rovnice funkcie f'(x) a dosaďte doň hodnotu bodu "a".
Vezmite všeobecnú tangentovú rovnicu, ktorá je definovaná ako y \u003d f (a) \u003d f (a) (x - a), a nahraďte nájdené hodnoty b, f (a), f "( a) do nej.V dôsledku toho sa nájde riešenie grafu a dotyčnica.
Vyriešte úlohu iným spôsobom, ak sa daný dotykový bod nezhoduje s dotykovým bodom. V tomto prípade je potrebné namiesto čísel v tangentovej rovnici dosadiť "a". Potom namiesto písmen "x" a "y" dosaďte hodnotu súradníc daného bodu. Vyriešte výslednú rovnicu, v ktorej "a" je neznáma. Výslednú hodnotu vložte do rovnice dotyčnice.
Napíšte rovnicu pre dotyčnicu s písmenom "a", ak je rovnica daná v podmienke úlohy funkcie a rovnicu rovnobežnej priamky vzhľadom na požadovanú dotyčnicu. Potom potrebujete derivát funkcie na súradnicu v bode „a“. Vložte príslušnú hodnotu do rovnice dotyčnice a vyriešte funkciu.