Dnes budeme hovoriť o logaritmické vzorce a dať demonštráciu príklady riešenia.

Samy o sebe implikujú vzory riešení podľa základných vlastností logaritmov. Pred použitím logaritmických vzorcov na riešenie si najprv pripomenieme všetky vlastnosti:

Teraz, na základe týchto vzorcov (vlastností), ukážeme príklady riešenia logaritmov.

Príklady riešenia logaritmov na základe vzorcov.

Logaritmus kladné číslo b v základe a (označené log a b) je exponent, na ktorý musí byť a umocnené, aby sme dostali b, pričom b > 0, a > 0 a 1.

Podľa definície log a b = x, čo je ekvivalent a x = b, teda log a a x = x.

Logaritmy, príklady:

log 2 8 = 3, pretože 2 3 = 8

log 7 49 = 2 pretože 72 = 49

log 5 1/5 = -1, pretože 5-1 = 1/5

Desatinný logaritmus je obyčajný logaritmus, ktorého základňa je 10. Označuje sa ako lg.

log 10 100 = 2 pretože 102 = 100

prirodzený logaritmus- tiež obvyklý logaritmus logaritmus, ale so základom e (e \u003d 2,71828 ... - iracionálne číslo). Označované ako ln.

Je vhodné si zapamätať vzorce alebo vlastnosti logaritmov, pretože ich budeme potrebovať neskôr pri riešení logaritmov, logaritmických rovníc a nerovníc. Prepracujme každý vzorec znova s ​​príkladmi.

• Základná logaritmická identita
  a log a b = b

  8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9

• Logaritmus súčinu sa rovná súčtu logaritmov
  log a (bc) = log a b + log a c

  log 3 8,1 + log 3 10 = log 3 (8,1 * 10) = log 3 81 = 4

• Logaritmus kvocientu sa rovná rozdielu logaritmov
  log a (b/c) = log a b - log a c

  9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81

• Vlastnosti stupňa logaritmovateľného čísla a základu logaritmu

  Exponent logaritmického čísla log a b m = mlog a b

  Exponent základu logaritmu log a n b =1/n*log a b

  log a n b m = m/n*log a b,

  ak m = n, dostaneme log a n b n = log a b

  log 4 9 = log 2 2 3 2 = log 2 3

• Prechod na nový základ
  log a b = log c b / log c a,

  ak c = b, dostaneme log b b = 1

  potom log a b = 1/log b a

  log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1

Ako vidíte, logaritmické vzorce nie sú také zložité, ako sa zdá. Teraz, keď sme zvážili príklady riešenia logaritmov, môžeme prejsť na logaritmické rovnice. Príklady riešenia logaritmických rovníc podrobnejšie zvážime v článku: "". Nenechajte si ujsť!

Ak máte stále otázky týkajúce sa riešenia, napíšte ich do komentárov k článku.

Poznámka: rozhodol som sa získať vzdelanie v inej triede štúdiom v zahraničí ako voliteľnú možnosť.

(z gréckeho λόγος - "slovo", "vzťah" a ἀριθμός - "číslo") b podľa rozumu a(log α b) sa nazýva takéto číslo c, a b= a c, teda log α b=c a b=ac sú rovnocenné. Logaritmus má zmysel, ak a > 0, a ≠ 1, b > 0.

Inými slovami logaritmusčísla b podľa rozumu a formulovaný ako exponent, na ktorý sa musí číslo zvýšiť a získať číslo b(logaritmus existuje len pre kladné čísla).

Z tejto formulácie vyplýva, že výpočet x= log α b, je ekvivalentné riešeniu rovnice a x =b.

Napríklad:

log 2 8 = 3 pretože 8 = 2 3 .

Upozorňujeme, že uvedená formulácia logaritmu umožňuje okamžite určiť logaritmickú hodnotu keď číslo pod znamienkom logaritmu je určitá mocnina základu. Formulácia logaritmu skutočne umožňuje zdôvodniť, že ak b = a c, potom logaritmus čísla b podľa rozumu a rovná sa s. Je tiež zrejmé, že téma logaritmu úzko súvisí s témou stupeň čísla.

Odvolávame sa na výpočet logaritmu logaritmus. Logaritmus je matematická operácia logaritmu. Pri logaritmovaní sa súčin faktorov transformuje na súčty členov.

Potencovanie je matematická operácia inverzná k logaritmu. Pri potenciácii sa daný základ pozdvihne na silu výrazu, na ktorom sa potenciácia vykonáva. V tomto prípade sa súčty členov transformujú na súčin faktorov.

Pomerne často sa používajú reálne logaritmy so základmi 2 (binárne), e Eulerovým číslom e ≈ 2,718 (prirodzený logaritmus) a 10 (desatinné).

V tejto fáze to stojí za zváženie vzorky logaritmov denník 7 2 , ln √ 5, lg0,0001.

A položky lg (-3), log -3 3,2, log -1 -4,3 nedávajú zmysel, pretože v prvom z nich je záporné číslo umiestnené pod znamienkom logaritmu, v druhom - záporné číslo v základ a v treťom - a záporné číslo pod znamienkom logaritmu a jednotky v základe.

Podmienky na určenie logaritmu.

Samostatne sa oplatí zvážiť podmienky a > 0, a ≠ 1, b > 0. definícia logaritmu. Pozrime sa, prečo sú tieto obmedzenia prijaté. To nám pomôže s rovnosťou tvaru x = log α b, nazývaná základná logaritmická identita, ktorá priamo vyplýva z definície logaritmu uvedenej vyššie.

Vezmite si podmienku a≠1. Keďže jedna sa rovná jednej akejkoľvek mocnine, potom rovnosť x=log α b môže existovať len vtedy b = 1, ale log 1 1 bude akékoľvek reálne číslo. Aby sme túto nejednoznačnosť odstránili, berieme a≠1.

Dokážme nevyhnutnosť podmienky a>0. O a=0 podľa formulácie logaritmu môže existovať len vtedy b = 0. A potom podľa toho log 0 0 môže byť akékoľvek nenulové reálne číslo, pretože nula až akákoľvek nenulová mocnina je nula. Na odstránenie tejto nejednoznačnosti podmienka a≠0. A kedy a<0 museli by sme odmietnuť analýzu racionálnych a iracionálnych hodnôt logaritmu, pretože exponent s racionálnym a iracionálnym exponentom je definovaný len pre nezáporné základy. Práve z tohto dôvodu je podmienka a>0.

A posledná podmienka b>0 vyplýva z nerovnosti a>0, pretože x=log α b, a hodnotu stupňa s kladným základom a vždy pozitívny.

Vlastnosti logaritmov.

Logaritmy vyznačujúce sa výrazným Vlastnosti, čo viedlo k ich širokému použitiu, čo výrazne uľahčilo starostlivé výpočty. Pri prechode „do sveta logaritmov“ sa násobenie premení na oveľa jednoduchšie sčítanie, delenie na odčítanie, umocňovanie a odmocňovanie na násobenie a delenie exponentom.

Formuláciu logaritmov a tabuľku ich hodnôt (pre goniometrické funkcie) prvýkrát publikoval v roku 1614 škótsky matematik John Napier. Logaritmické tabuľky, rozšírené a podrobné inými vedcami, boli široko používané vo vedeckých a technických výpočtoch a zostali relevantné, kým sa nezačali používať elektronické kalkulačky a počítače.

Vo vzťahu k

možno nastaviť úlohu nájsť ľubovoľné z troch čísel z ostatných dvoch, ktoré sú dané. Dané a a potom N sa zistí umocnením. Ak je dané N a potom sa a nájde extrahovaním odmocniny x (alebo umocnením). Teraz zvážte prípad, keď je za dané a a N potrebné nájsť x.

Nech je číslo N kladné: číslo a je kladné a nerovná sa jednej: .

Definícia. Logaritmus čísla N k základu a je exponent, na ktorý musíte zvýšiť a, aby ste dostali číslo N; logaritmus je označený

V rovnosti (26.1) sa teda exponent nachádza ako logaritmus N k základu a. Príspevky

majú rovnaký význam. Rovnosť (26.1) sa niekedy nazýva základná identita teórie logaritmov; v skutočnosti vyjadruje definíciu pojmu logaritmus. Podľa tejto definície je základ logaritmu a vždy kladný a odlišný od jednoty; logaritmovateľné číslo N je kladné. Záporné čísla a nula nemajú logaritmy. Dá sa dokázať, že každé číslo s daným základom má dobre definovaný logaritmus. Preto rovnosť znamená . Všimnite si, že podmienka je tu nevyhnutná, inak by záver nebol opodstatnený, pretože rovnosť platí pre všetky hodnoty x a y.

Príklad 1. Nájdite

rozhodnutie. Ak chcete získať číslo, musíte zvýšiť základ 2 na silu Preto.

Pri riešení takýchto príkladov môžete zaznamenať v nasledujúcom formulári:

Príklad 2. Nájdite .

rozhodnutie. Máme

V príkladoch 1 a 2 sme ľahko našli požadovaný logaritmus reprezentovaním logaritmovateľného čísla ako stupňa základne s racionálnym exponentom. Vo všeobecnom prípade, napríklad pre atď., to nemožno urobiť, pretože logaritmus má iracionálnu hodnotu. Venujme pozornosť jednej otázke súvisiacej s týmto tvrdením. V § 12 sme uviedli pojem možnosti určenia ľubovoľnej reálnej mocniny daného kladného čísla. Bolo to potrebné na zavedenie logaritmov, ktoré vo všeobecnosti môžu byť iracionálne čísla.

Zvážte niektoré vlastnosti logaritmov.

Vlastnosť 1. Ak sa číslo a základ rovnajú, potom sa logaritmus rovná jednej, a naopak, ak sa logaritmus rovná jednej, potom sa číslo a základ rovnajú.

Dôkaz. Nech Podľa definície logaritmu máme a odkiaľ

Naopak, nech Potom podľa definície

Vlastnosť 2. Logaritmus jednoty k ľubovoľnej základni sa rovná nule.

Dôkaz. Podľa definície logaritmu (nulová mocnina ľubovoľnej kladnej bázy sa rovná jednej, pozri (10.1)). Odtiaľ

Q.E.D.

Platí aj opačné tvrdenie: ak , potom N = 1. V skutočnosti máme .

Pred uvedením nasledujúcej vlastnosti logaritmov sa dohodneme, že dve čísla a a b ležia na rovnakej strane tretieho čísla c, ak sú obe väčšie ako c alebo menšie ako c. Ak je jedno z týchto čísel väčšie ako c a druhé menšie ako c, potom hovoríme, že ležia na opačných stranách c.

Vlastnosť 3. Ak číslo a základ ležia na rovnakej strane jednoty, potom je logaritmus kladný; ak číslo a základ ležia na opačných stranách jednoty, potom je logaritmus záporný.

Dôkaz vlastnosti 3 je založený na skutočnosti, že stupeň a je väčší ako jedna, ak je základ väčší ako jeden a exponent je kladný, alebo ak je základ menší ako jeden a exponent je záporný. Stupeň je menší ako jedna, ak je základ väčší ako jedna a exponent je záporný, alebo ak je základ menší ako jedna a exponent je kladný.

Do úvahy prichádzajú štyri prípady:

Obmedzíme sa na rozbor prvého z nich, zvyšok si čitateľ zváži sám.

Nech potom exponent v rovnosti nie je ani záporný, ani rovný nule, teda je kladný, t.j., ktorý bolo potrebné dokázať.

Príklad 3. Zistite, ktoré z nasledujúcich logaritmov sú kladné a ktoré záporné:

Riešenie, a) keďže číslo 15 a základňa 12 sú umiestnené na rovnakej strane jednotky;

b) , keďže 1000 a 2 sú umiestnené na tej istej strane jednotky; zároveň nie je podstatné, že základ je väčší ako logaritmické číslo;

c), keďže 3,1 a 0,8 ležia na opačných stranách jednoty;

G); prečo?

e) ; prečo?

Nasledujúce vlastnosti 4-6 sa často nazývajú pravidlá logaritmu: umožňujú, poznajúc logaritmy niektorých čísel, nájsť logaritmy ich súčinu, kvocient, stupeň každého z nich.

Vlastnosť 4 (pravidlo pre logaritmus súčinu). Logaritmus súčinu niekoľkých kladných čísel v danom základe sa rovná súčtu logaritmov týchto čísel v rovnakom základe.

Dôkaz. Nech sú uvedené kladné čísla.

Pre logaritmus ich súčinu napíšeme rovnosť (26.1) definujúcu logaritmus:

Odtiaľto nájdeme

Porovnaním exponentov prvého a posledného výrazu získame požadovanú rovnosť:

Všimnite si, že podmienka je nevyhnutná; logaritmus súčinu dvoch záporných čísel dáva zmysel, ale v tomto prípade dostaneme

Vo všeobecnosti, ak je súčin viacerých faktorov kladný, potom sa jeho logaritmus rovná súčtu logaritmov modulov týchto faktorov.

Vlastnosť 5 (pravidlo kvocientového logaritmu). Logaritmus podielu kladných čísel sa rovná rozdielu medzi logaritmami dividendy a deliteľa v rovnakom základe. Dôkaz. Dôsledne nájsť

Q.E.D.

Vlastnosť 6 (pravidlo logaritmu stupňa). Logaritmus mocniny ľubovoľného kladného čísla sa rovná logaritmu tohto čísla krát exponent.

Dôkaz. K číslu opäť napíšeme hlavnú identitu (26.1):

Q.E.D.

Dôsledok. Logaritmus odmocniny kladného čísla sa rovná logaritmu odmocniny vydelenému exponentom odmocniny:

Platnosť tohto následku môžeme dokázať prezentáciou ako a použitím vlastnosti 6.

Príklad 4. Logaritmus na základ a:

a) (predpokladá sa, že všetky hodnoty b, c, d, e sú kladné);

b) (predpokladá sa, že ).

Riešenie a) V tomto výraze je vhodné prejsť na zlomkové mocniny:

Na základe rovnosti (26,5)-(26,7) môžeme teraz napísať:

Všimli sme si, že s logaritmami čísel sa vykonávajú jednoduchšie operácie ako s číslami samotnými: pri násobení čísel sa ich logaritmy sčítajú, pri delení sa odčítajú atď.

Preto sa vo výpočtovej praxi používajú logaritmy (pozri § 29).

Akcia inverzná k logaritmu sa nazýva potenciácia, menovite: potenciácia je akcia, pri ktorej sa toto číslo samo nájde daným logaritmom čísla. V podstate potenciácia nie je žiadna špeciálna akcia: ide o zvýšenie základne na mocninu (rovnajúcu sa logaritmu čísla). Pojem "potenciácia" možno považovať za synonymum pojmu "umocnenie".

Pri potenciácii je potrebné použiť pravidlá, ktoré sú inverzné k pravidlám logaritmu: nahradiť súčet logaritmov logaritmom súčinu, rozdiel logaritmov logaritmom kvocientu atď. Najmä ak existuje akýkoľvek faktor pred znamienkom logaritmu, potom sa musí pri potenciácii preniesť na stupne indikátora pod znamienkom logaritmu.

Príklad 5. Nájdite N, ak je to známe

rozhodnutie. V súvislosti s práve uvedeným potenciačným pravidlom sa faktory 2/3 a 1/3, ktoré sú pred znamienkami logaritmov na pravej strane tejto rovnosti, prenesú na exponenty pod znamienkami týchto logaritmov; dostaneme

Teraz nahradíme rozdiel logaritmov logaritmom kvocientu:

aby sme získali posledný zlomok v tomto reťazci rovnosti, oslobodili sme predchádzajúci zlomok od iracionality v menovateli (časť 25).

Vlastnosť 7. Ak je základ väčší ako jedna, potom väčšie číslo má väčší logaritmus (a menšie má menší), ak je základ menší ako jeden, potom väčšie číslo má menší logaritmus (a menšie jeden má väčší).

Táto vlastnosť je tiež formulovaná ako pravidlo pre logaritmus nerovností, ktorých obe časti sú kladné:

Pri logaritmovaní nerovností so základom väčším ako jedna sa zachová znamienko nerovnosti a pri logaritmovaní so základom menším ako jedna sa znamienko nerovnosti obráti (pozri aj bod 80).

Dôkaz je založený na vlastnostiach 5 a 3. Uvažujme prípad, keď If , then a s použitím logaritmu dostaneme

(a a N/M ležia na rovnakej strane jednoty). Odtiaľ

Ak bude nasledovať, čitateľ na to príde sám.

Definícia logaritmu

Logaritmus čísla b k základu a je exponent, na ktorý musíte zvýšiť a, aby ste dostali b.

Číslo e v matematike je zvykom označovať hranicu, ku ktorej výraz smeruje

Číslo e je iracionálne číslo- číslo neporovnateľné s jednotkou, nedá sa presne vyjadriť ani ako celok, ani ako zlomok racionálnyčíslo.

List e- prvé písmeno latinského slova exonere- chváliť sa, odtiaľ názov v matematike exponenciálny- exponenciálna funkcia.

číslo eširoko používané v matematike a vo všetkých vedách, tak či onak využívajúce matematické výpočty pre svoje potreby.

Logaritmy. Vlastnosti logaritmov

Definícia: Základný logaritmus kladného čísla b je exponent c, na ktorý sa musí číslo a zvýšiť, aby sa získalo číslo b.

Základná logaritmická identita:

7) Vzorec pre prechod na nový základ:

lna = log e a, e ≈ 2,718…

Úlohy a testy na tému „Logaritmy. Vlastnosti logaritmov»

• Logaritmy - Dôležité témy pre opakovanie skúšky z matematiky

Ak chcete úspešne dokončiť úlohy na túto tému, musíte poznať definíciu logaritmu, vlastnosti logaritmov, základnú logaritmickú identitu, definície desiatkových a prirodzených logaritmov. Hlavnými typmi úloh na túto tému sú úlohy na výpočet a prevod logaritmických výrazov. Uvažujme o ich riešení na nasledujúcich príkladoch.

rozhodnutie: Pomocou vlastností logaritmov dostaneme

rozhodnutie: pomocou vlastností stupňa dostaneme

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Vlastnosti logaritmov, formulácií a dôkazov.

Logaritmy majú množstvo charakteristických vlastností. V tomto článku budeme analyzovať hlavné vlastnosti logaritmov. Tu uvádzame ich formulácie, zapisujeme vlastnosti logaritmov vo forme vzorcov, uvádzame príklady ich použitia a tiež uvádzame dôkazy o vlastnostiach logaritmov.

Navigácia na stránke.

Základné vlastnosti logaritmov, vzorce

Pre ľahké zapamätanie a používanie uvádzame základné vlastnosti logaritmov ako zoznam vzorcov. V ďalšej časti uvádzame ich formulácie, dôkazy, príklady použitia a potrebné vysvetlenia.

Vlastnosť denníka jednotiek: log a 1=0 pre ľubovoľné a>0 , a≠1 .

Logaritmus čísla rovného základu: log a a=1 pre a>0 , a≠1 .

Vlastnosť logaritmu základného stupňa: log a a p =p , kde a>0 , a≠1 a p je ľubovoľné reálne číslo.

Logaritmus súčinu dvoch kladných čísel: log a (x y) = log a x + log a y , a>0 , a≠1 , x>0 , y>0 ,
a vlastnosť logaritmu súčinu n kladných čísel: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a> 0, a≠1 , x 1 > 0, x 2 > 0, ..., xn > 0 .

Vlastnosť súkromného logaritmu: , kde a>0, a≠1, x>0, y>0.

Logaritmus mocniny čísla: log a b p =p log a |b| , kde a>0 , a≠1, b a p sú čísla také, že stupeň b p dáva zmysel a b p > 0 .

Dôsledok: , kde a>0 , a≠1 , n je prirodzené číslo väčšie ako jedna, b>0 .

Dôsledok 1: , a>0, a≠1, b>0, b≠1.

Dôsledok 2: , a>0 , a≠1 , b>0 , p a q sú reálne čísla, q≠0 , konkrétne pre b=a máme .

Výkazy a doklady o vlastnostiach

Prejdeme k formulácii a dôkazu zaznamenaných vlastností logaritmov. Všetky vlastnosti logaritmov sa dokazujú na základe definície logaritmu a základnej logaritmickej identity, ktorá z neho vyplýva, ako aj vlastností stupňa.

Začnime s vlastnosti logaritmu jednoty. Jeho formulácia je nasledovná: logaritmus jednoty sa rovná nule, tj. log a 1=0 pre ľubovoľné a>0, a≠1. Dôkaz je jednoduchý: keďže a 0 = 1 pre ľubovoľné a, ktoré spĺňa vyššie uvedené podmienky a>0 a a≠1 , potom z definície logaritmu okamžite vyplýva dokázaná rovnosť log a 1=0.

Uveďme príklady aplikácie uvažovanej vlastnosti: log 3 1=0 , lg1=0 a .

Prejdime k ďalšej vlastnosti: logaritmus čísla rovného základu sa rovná jednej, teda log a a=1 pre a>0, a≠1. V skutočnosti, keďže a 1 =a pre ľubovoľné a , potom podľa definície logaritmu log a a=1 .

Príklady použitia tejto vlastnosti logaritmov sú log 5 5 = 1 , log 5,6 5,6 a lne = 1 .

Logaritmus mocniny čísla rovného základu logaritmu sa rovná exponentu. Táto vlastnosť logaritmu zodpovedá vzorcu formulára log a a p =p, kde a>0 , a≠1 a p je ľubovoľné reálne číslo. Táto vlastnosť vyplýva priamo z definície logaritmu. Všimnite si, že vám umožňuje okamžite určiť hodnotu logaritmu, ak je možné reprezentovať číslo pod znamienkom logaritmu ako stupeň základne, o tom budeme hovoriť viac v článku Výpočet logaritmov.

Napríklad log 2 2 7 =7, log10-4 =-4 a .

Logaritmus súčinu dvoch kladných čísel x a y sa rovná súčinu logaritmov týchto čísel: log a (x y)=log a x+log a y, a>0, a≠1. Dokážme vlastnosť logaritmu súčinu. Vzhľadom na vlastnosti stupňa a log a x + log a y = a log a x a log a y , a keďže podľa hlavnej logaritmickej identity log a x =x a log a y = y , potom log a x a log a y =x y . Teda log a x + log a y = x y , z čoho vyplýva požadovaná rovnosť podľa definície logaritmu.

Ukážme si príklady použitia vlastnosti logaritmu súčinu: log 5 (2 3)=log 5 2+log 5 3 a .

Vlastnosť logaritmu súčinu možno zovšeobecniť na súčin konečného počtu n kladných čísel x 1 , x 2 , …, x n ako log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Táto rovnosť sa dá ľahko dokázať metódou matematickej indukcie.

Napríklad prirodzený logaritmus súčinu možno nahradiť súčtom troch prirodzených logaritmov čísel 4 , e a .

Logaritmus podielu dvoch kladných čísel x a y sa rovná rozdielu medzi logaritmami týchto čísel. Vlastnosť kvocientového logaritmu zodpovedá vzorcu tvaru , kde a>0 , a≠1 , x a y sú nejaké kladné čísla. Platnosť tohto vzorca je dokázaná ako vzorec pre logaritmus súčinu: od , potom podľa definície logaritmu .

Tu je príklad použitia tejto vlastnosti logaritmu: .

Prejdime k vlastnosť logaritmu stupňa. Logaritmus stupňa sa rovná súčinu exponentu a logaritmu modulu bázy tohto stupňa. Túto vlastnosť logaritmu stupňa zapíšeme vo forme vzorca: log a b p =p log a |b|, kde a>0 , a≠1, b a p sú čísla také, že stupeň b p dáva zmysel a b p > 0 .

Najprv dokážeme túto vlastnosť pre kladné b . Základná logaritmická identita nám umožňuje reprezentovať číslo b ako log a b , potom b p = (a log a b) p a výsledný výraz sa vďaka vlastnosti mocniny rovná a p log a b . Dostaneme sa teda k rovnosti b p =a p log a b , z ktorej podľa definície logaritmu usúdime, že log a b p = p log a b .

Zostáva dokázať túto vlastnosť pre záporné b . Tu si všimneme, že výraz log a b p pre záporné b má zmysel len pre párne exponenty p (keďže hodnota stupňa b p musí byť väčšia ako nula, inak logaritmus nebude dávať zmysel) a v tomto prípade b p =|b| p . Potom b p =|b| p =(a log a |b|) p =a p log a |b| , odkiaľ log a b p =p log a |b| .

Napríklad, a ln(-3)4=4ln|-3|=4ln3.

Vyplýva to z predchádzajúcej vlastnosti vlastnosť logaritmu od koreňa: logaritmus odmocniny n-tého stupňa sa rovná súčinu zlomku 1/n a logaritmu koreňového výrazu, teda kde a>0, a≠1, n je prirodzené číslo väčšie ako jedna, b>0.

Dôkaz je založený na rovnosti (pozri definíciu exponentu so zlomkovým exponentom), ktorá platí pre každé kladné b , a vlastnosti logaritmu stupňa: .

Tu je príklad použitia tejto vlastnosti: .

Teraz dokážme prevodný vzorec na nový základ logaritmu milý . Na to stačí dokázať platnosť log c b = log a b log c a . Základná logaritmická identita nám umožňuje reprezentovať číslo b ako log a b , potom log c b = log c a log a b . Zostáva použiť vlastnosť logaritmu stupňa: log c a log a b = log a b log c a . Rovnosť log c b=log a b log c a je teda dokázaná, čo znamená, že je dokázaný aj vzorec na prechod na nový základ logaritmu. .

Ukážme si niekoľko príkladov použitia tejto vlastnosti logaritmov: a .

Vzorec na prechod na novú základňu vám umožňuje prejsť na prácu s logaritmami, ktoré majú „pohodlnú“ základňu. Napríklad sa dá použiť na prepnutie na prirodzené alebo desiatkové logaritmy, aby ste mohli vypočítať hodnotu logaritmu z tabuľky logaritmov. Vzorec na prechod na nový základ logaritmu tiež umožňuje v niektorých prípadoch nájsť hodnotu daného logaritmu, keď sú známe hodnoty niektorých logaritmov s inými základmi.

Často sa používa špeciálny prípad prechodového vzorca na nový základ logaritmu pre c=b tvaru. To ukazuje, že log a b a log b a sú vzájomne inverzné čísla. napr. .

Vzorec sa tiež často používa, čo je výhodné pri hľadaní logaritmických hodnôt. Aby sme potvrdili naše slová, ukážeme, ako sa pomocou neho vypočíta hodnota logaritmu formulára. Máme . Na dôkaz vzorca stačí použiť prechodový vzorec na nový základ logaritmu a: .

Zostáva dokázať porovnávacie vlastnosti logaritmov.

Použime opačnú metódu. Predpokladajme, že pre a 1 > 1 , a 2 > 1 a a 1 2 a pre 0 1 log a 1 b≤ log a 2 b platí. Pomocou vlastností logaritmov možno tieto nerovnosti prepísať ako a v uvedenom poradí a z nich vyplýva, že log b a 1 ≤ log b a 2 a log b a 1 ≥ log b a 2, v tomto poradí. Potom, pomocou vlastností mocnín s rovnakými základmi, musia byť splnené rovnosti b log b a 1 ≥ b log b a 2 a b log b a 1 ≥ b log b a 2, teda a 1 ≥a 2 . Dospeli sme teda k rozporu s podmienkou a 1 2 . Tým je dôkaz hotový.

Základné vlastnosti logaritmov

• Materiály na lekciu
• Stiahnite si všetky vzorce

Logaritmy, ako každé číslo, možno sčítať, odčítať a previesť všetkými možnými spôsobmi. Ale keďže logaritmy nie sú celkom bežné čísla, existujú tu pravidlá, ktoré sa nazývajú základné vlastnosti.

Tieto pravidlá musia byť známe - bez nich nemožno vyriešiť žiadny vážny logaritmický problém. Navyše je ich veľmi málo – všetko sa dá naučiť za jeden deň. Tak poďme na to.

Sčítanie a odčítanie logaritmov

Uvažujme dva logaritmy s rovnakým základom: log a x a log a y . Potom ich možno sčítať a odčítať a:

Súčet logaritmov sa teda rovná logaritmu súčinu a rozdiel je logaritmus kvocientu. Poznámka: kľúčovým bodom je tu - rovnaké dôvody. Ak sú základy odlišné, tieto pravidlá nefungujú!

Tieto vzorce pomôžu vypočítať logaritmický výraz, aj keď sa neberú do úvahy jeho jednotlivé časti (pozri lekciu „Čo je logaritmus“). Pozrite sa na príklady - a uvidíte:

Úloha. Nájdite hodnotu výrazu: log 6 4 + log 6 9.

Keďže základy logaritmov sú rovnaké, použijeme súčtový vzorec:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Úloha. Nájdite hodnotu výrazu: log 2 48 − log 2 3.

Základy sú rovnaké, používame rozdielový vzorec:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Úloha. Nájdite hodnotu výrazu: log 3 135 − log 3 5.

Opäť platí, že základy sú rovnaké, takže máme:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Ako vidíte, pôvodné výrazy sa skladajú zo „zlých“ logaritmov, ktoré sa neuvažujú samostatne. Ale po transformáciách sa ukážu celkom normálne čísla. Mnohé testy sú založené na tejto skutočnosti. Áno, tá kontrola – podobné výrazy vo všetkej vážnosti (niekedy – prakticky bez zmien) sa ponúkajú na skúške.

Odstránenie exponentu z logaritmu

Teraz si úlohu trochu skomplikujeme. Čo ak existuje stupeň v základe alebo argumente logaritmu? Potom môže byť exponent tohto stupňa vyňatý zo znamienka logaritmu podľa nasledujúcich pravidiel:

• log a x n = n log a x ;
• 
• 

Je ľahké vidieť, že posledné pravidlo nasleduje ich prvé dve. Ale je lepšie si to aj tak zapamätať – v niektorých prípadoch to výrazne zníži množstvo výpočtov.

Všetky tieto pravidlá majú samozrejme zmysel, ak sa dodrží logaritmus ODZ: a > 0, a ≠ 1, x > 0. A ešte niečo: naučte sa aplikovať všetky vzorce nielen zľava doprava, ale aj naopak, t.j. môžete zadať čísla pred znamienkom logaritmu do samotného logaritmu. To je to, čo sa najčastejšie vyžaduje.

Úloha. Nájdite hodnotu výrazu: log 7 49 6 .

Zbavme sa stupňa v argumente podľa prvého vzorca:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Úloha. Nájdite hodnotu výrazu:

[Titul obrázku]

Všimnite si, že menovateľ je logaritmus, ktorého základ a argument sú presné mocniny: 16 = 2 4 ; 49 = 72. Máme:

[Titul obrázku]

Myslím, že posledný príklad potrebuje objasnenie. Kam zmizli logaritmy? Do poslednej chvíle pracujeme len s menovateľom. Predložili základ a argument tam stojaceho logaritmu vo forme stupňov a vybrali ukazovatele - dostali „trojposchodový“ zlomok.

Teraz sa pozrime na hlavný zlomok. Čitateľ a menovateľ majú rovnaké číslo: log 2 7. Keďže log 2 7 ≠ 0, zlomok môžeme zmenšiť - 2/4 zostanú v menovateli. Podľa pravidiel aritmetiky môžu byť štyri prenesené do čitateľa, čo sa stalo. Výsledkom je odpoveď: 2.

Prechod na nový základ

Keď už hovoríme o pravidlách sčítania a odčítania logaritmov, osobitne som zdôraznil, že fungujú iba s rovnakými základmi. Čo ak sú základy odlišné? Čo ak to nie sú presné mocniny rovnakého čísla?

Na pomoc prichádzajú vzorce pre prechod na novú základňu. Formulujeme ich vo forme vety:

Nech je daný logaritmus log a x. Potom pre akékoľvek číslo c také, že c > 0 a c ≠ 1, platí rovnosť:

[Titul obrázku]

Konkrétne, ak dáme c = x , dostaneme:

[Titul obrázku]

Z druhého vzorca vyplýva, že je možné zameniť základ a argument logaritmu, ale v tomto prípade je celý výraz „prevrátený“, t.j. logaritmus je v menovateli.

Tieto vzorce sa zriedka nachádzajú v bežných číselných výrazoch. Ich vhodnosť je možné vyhodnotiť len pri riešení logaritmických rovníc a nerovníc.

Sú však úlohy, ktoré sa nedajú vyriešiť vôbec inak ako presťahovaním sa do nového základu. Uvažujme o niekoľkých z nich:

Úloha. Nájdite hodnotu výrazu: log 5 16 log 2 25.

Všimnite si, že argumenty oboch logaritmov sú presné exponenty. Vyberme ukazovatele: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Teraz otočme druhý logaritmus:

[Titul obrázku]

Keďže súčin sa nemení permutáciou faktorov, pokojne sme vynásobili štyri a dva a potom sme prišli na logaritmy.

Úloha. Nájdite hodnotu výrazu: log 9 100 lg 3.

Základom a argumentom prvého logaritmu sú presné mocniny. Poďme si to zapísať a zbaviť sa indikátorov:

[Titul obrázku]

Teraz sa zbavme desiatkového logaritmu prechodom na nový základ:

[Titul obrázku]

Základná logaritmická identita

V procese riešenia je často potrebné reprezentovať číslo ako logaritmus k danej báze. V tomto prípade nám pomôžu vzorce:

1. n = log a a n

2. V prvom prípade sa číslo n stane exponentom v argumente. Číslo n môže byť úplne čokoľvek, pretože je to len hodnota logaritmu.

   Druhý vzorec je vlastne parafrázovaná definícia. Nazýva sa to základná logaritmická identita.

   Čo sa vlastne stane, ak číslo b umocníme na takú mocninu, že číslo b s touto mocninou dá číslo a? Správne: toto je rovnaké číslo a . Ešte raz si pozorne prečítajte tento odsek – veľa ľudí na ňom „visí“.

   Rovnako ako nové základné konverzné vzorce, základná logaritmická identita je niekedy jediným možným riešením.

   [Titul obrázku]

   Všimnite si, že log 25 64 = log 5 8 - stačí vziať druhú mocninu základne a argument logaritmu. Vzhľadom na pravidlá násobenia právomocí s rovnakým základom dostaneme:

   [Titul obrázku]

   Ak niekto nevie, toto bola skutočná úloha z Jednotnej štátnej skúšky 🙂

   Logaritmická jednotka a logaritmická nula

   Na záver uvediem dve identity, ktoré je ťažké nazvať vlastnosťami – skôr ide o dôsledky z definície logaritmu. Neustále sa nachádzajú v problémoch a prekvapivo robia problémy aj „pokročilým“ žiakom.

   1. log a a = 1 je logaritmická jednotka. Pamätajte si raz a navždy: logaritmus k ľubovoľnej základni a z tejto samotnej základne sa rovná jednej.
   2. log a 1 = 0 je logaritmická nula. Základom a môže byť čokoľvek, ale ak je argument jedna - logaritmus je nula! Pretože a 0 = 1 je priamym dôsledkom definície.

   To sú všetky vlastnosti. Určite si ich nacvičte v praxi! Stiahnite si cheat sheet na začiatku lekcie, vytlačte si ho - a vyriešte problémy.

   Logaritmus. Vlastnosti logaritmu (sčítanie a odčítanie).

   Vlastnosti logaritmu vyplýva z jeho definície. A teda logaritmus čísla b podľa rozumu a definovaný ako exponent, na ktorý sa musí číslo zvýšiť a získať číslo b(logaritmus existuje len pre kladné čísla).

   Z tejto formulácie vyplýva, že výpočet x=log a b, je ekvivalentné riešeniu rovnice ax=b. Napríklad, log 2 8 = 3 pretože 8 = 2 3 . Formulácia logaritmu umožňuje zdôvodniť, že ak b = a c, potom logaritmus čísla b podľa rozumu a rovná sa s. Je tiež zrejmé, že téma logaritmu úzko súvisí s témou sily čísla.

   S logaritmami, ako s akýmikoľvek číslami, môžete vykonávať operácie sčítania, odčítania a transformovať všetkými možnými spôsobmi. Ale vzhľadom na to, že logaritmy nie sú celkom bežné čísla, platia tu ich vlastné špeciálne pravidlá, tzv. základné vlastnosti.

   Sčítanie a odčítanie logaritmov.

   Vezmite dva logaritmy s rovnakým základom: log x a prihlásiť sa y. Potom je možné vykonať operácie sčítania a odčítania:

   Ako vidíme, súčet logaritmov sa rovná logaritmu súčinu a rozdiel logaritmy- logaritmus podielu. A to je pravda, ak čísla a, X a pri pozitívne a a ≠ 1.

   Je dôležité poznamenať, že hlavným aspektom v týchto vzorcoch sú rovnaké základy. Ak sa bázy navzájom líšia, tieto pravidlá neplatia!

   Pravidlá pre sčítanie a odčítanie logaritmov s rovnakými základmi sa čítajú nielen zľava doprava, ale aj naopak. Výsledkom je, že máme vety pre logaritmus súčinu a logaritmus kvocientu.

   Logaritmus produktu dve kladné čísla sa rovnajú súčtu ich logaritmov ; parafrázovaním tejto vety dostaneme nasledovné, ak čísla a, X a pri pozitívne a a ≠ 1, potom:

   Logaritmus kvocientu dvoch kladných čísel sa rovná rozdielu medzi logaritmami dividendy a deliteľa. Inými slovami, ak čísla a, X a pri pozitívne a a ≠ 1, potom:

   Na riešenie použijeme vyššie uvedené vety príklady:

   Ak čísla X a pri sú teda negatívne vzorec na logaritmus produktu stáva bezvýznamným. Preto je zakázané písať:

   keďže výrazy log 2 (-8) a log 2 (-4) nie sú vôbec definované (logaritmická funkcia pri= log 2 X definované len pre kladné hodnoty argumentu X).

   Veta o produkte platí nielen pre dva, ale aj pre neobmedzený počet faktorov. To znamená, že pre každého prírodného k a akékoľvek kladné čísla X 1 , X 2 , . . . ,x n existuje identita:

   Od kvocientové logaritmické vety možno získať ešte jednu vlastnosť logaritmu. Je dobre známe, že log a 1 = 0, teda

   Existuje teda rovnosť:

   Logaritmy dvoch vzájomne recipročných čísel na rovnakom základe sa budú od seba líšiť iba znakom. Takže:

   Logaritmus. Vlastnosti logaritmov

   Logaritmus. Vlastnosti logaritmov

   Zvážte rovnosť. Dajte nám vedieť hodnoty a my chceme nájsť hodnotu .

   To znamená, že hľadáme exponenta, ku ktorému sa musíte natiahnuť, aby ste sa dostali .

   Nechať byť premenná môže nadobúdať akúkoľvek skutočnú hodnotu, potom sa na premenné vzťahujú nasledujúce obmedzenia: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Ak poznáme hodnoty a a stojíme pred úlohou nájsť neznáme, potom sa na tento účel zavádza matematická operácia, ktorá sa nazýva logaritmus.

   Aby sme našli hodnotu, ktorú berieme logaritmus čísla na nadácie :

   Logaritmus čísla k základu je exponent, na ktorý musíte zvýšiť, aby ste sa dostali .

   Teda základná logaritmická identita:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   je v podstate matematický zápis definície logaritmu.

   Logaritmus matematickej operácie je prevrátená hodnota umocňovania, tzn vlastnosti logaritmovúzko súvisia s vlastnosťami stupňa.

   Uvádzame hlavné vlastnosti logaritmov:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   Nasledujúca skupina vlastností vám umožňuje reprezentovať exponent výrazu pod znamienkom logaritmu alebo stojacim na základni logaritmu ako koeficient pred znamienkom logaritmu:

   6.

   7.

   8.

   9.

   Ďalšia skupina vzorcov vám umožňuje prejsť od logaritmu s daným základom k logaritmu s ľubovoľným základom a je tzv. prechodové vzorce na nový základ:

   10.

   12. (dôsledok vlastnosti 11)

   

   Nasledujúce tri vlastnosti nie sú dobre známe, ale často sa používajú pri riešení logaritmických rovníc alebo pri zjednodušovaní výrazov obsahujúcich logaritmy:

   13.

   14.

   15.

   Špeciálne prípady:

   — desiatkový logaritmus

   — prirodzený logaritmus

   Pri zjednodušovaní výrazov obsahujúcich logaritmy sa uplatňuje všeobecný prístup:

   1. Desatinné zlomky predstavujeme vo forme obyčajných.

   2. Zmiešané čísla reprezentujeme ako nevlastné zlomky.

   3. Čísla na báze logaritmu a pod znamienkom logaritmu sa rozložia na prvočísla.

   4. Snažíme sa priviesť všetky logaritmy na rovnakú základňu.

   5. Použite vlastnosti logaritmov.

   Pozrime sa na príklady zjednodušenia výrazov obsahujúcich logaritmy.

   Príklad 1

   Vypočítať:

   Zjednodušme všetky exponenty: našou úlohou je uviesť ich do logaritmov, ktorých základňa je rovnaké číslo ako základ exponentu.

   ==(podľa vlastnosti 7)=(podľa vlastnosti 6) =

   Dosaďte ukazovatele, ktoré sme získali v pôvodnom výraze. Dostaneme:

   Odpoveď: 5.25

   Príklad 2 Vypočítajte:

   

   Všetky logaritmy privedieme na základ 6 (v tomto prípade logaritmy z menovateľa zlomku „migrujú“ do čitateľa):

   Rozložme čísla pod znamienkom logaritmu na prvočísla:

   Použite vlastnosti 4 a 6:

   Predstavujeme náhradu

   Dostaneme:

   odpoveď: 1

   Logaritmus . Základná logaritmická identita.

   Vlastnosti logaritmov. Desatinný logaritmus. prirodzený logaritmus.

   logaritmus kladné číslo N v zákl (b > 0, b 1) sa nazýva exponent x, na ktorý musíte zvýšiť b, aby ste dostali N .

   Tento záznam je ekvivalentný nasledujúcemu: b x = N .

   PRÍKLADY: log 3 81 = 4, pretože 3 4 = 81 ;

   log 1/3 27 = – 3, pretože (1/3) - 3 = 3 3 = 27 .

   Vyššie uvedená definícia logaritmu môže byť napísaná ako identita:

   

   Základné vlastnosti logaritmov.

   2) log 1 = 0, pretože b 0 = 1 .

   3) Logaritmus súčinu sa rovná súčtu logaritmov faktorov:

   4) Logaritmus podielu sa rovná rozdielu medzi logaritmami dividendy a deliteľa:

   5) Logaritmus stupňa sa rovná súčinu exponentu a logaritmu jeho základne:

   Dôsledkom tejto vlastnosti je nasledovné: log root rovná sa logaritmu čísla odmocniny vydeleného mocninou odmocniny:

   

   6) Ak je základom logaritmu stupeň, potom hodnota prevrátenú hodnotu exponentu možno zo znaku denníka rýmov odstrániť:

   

   Posledné dve vlastnosti je možné spojiť do jednej:

   

   7) Vzorec pre prechodový modul (t. j. prechod z jednej bázy logaritmu na druhú bázu):

   

   V konkrétnom prípade, kedy N = a máme:

   

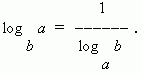
   Desatinný logaritmus volal základný logaritmus 10. Označuje sa lg, t.j. denník 10 N= log N. Logaritmy čísel 10, 100, 1000, . p sú 1, 2, 3, …, t.j. mať veľa pozitívnych

   jednotiek, koľko núl je v logaritmickom čísle po jednotke. Logaritmy čísel 0,1, 0,01, 0,001, . p sú –1, –2, –3, …, t.j. mať toľko záporných jednotiek, koľko je núl v logaritmickom čísle pred jednotkou (vrátane nulových celých čísel). Logaritmy zostávajúcich čísel majú tzv. zlomkovú časť mantisa. Volá sa celočíselná časť logaritmu charakteristický. Pre praktické aplikácie sú najvhodnejšie desiatkové logaritmy.

   prirodzený logaritmus volal základný logaritmus e. Označuje sa ln, t.j. log e N=ln N. číslo e je iracionálna, jej približná hodnota je 2,718281828. Je to hranica, ku ktorej sa číslo (1 + 1 / n) n s neobmedzeným nárastom n(cm. prvá úžasná limitka na stránke Limity číselnej postupnosti).
   Aj keď sa to môže zdať zvláštne, prirodzené logaritmy sa ukázali ako veľmi vhodné pri vykonávaní rôznych operácií súvisiacich s analýzou funkcií. Výpočet základných logaritmov e oveľa rýchlejšie ako akýkoľvek iný základ.

• Čo dnes potrebujete na adopciu dieťaťa v Rusku? Adopcia v Rusku okrem zodpovedného osobného rozhodnutia zahŕňa aj množstvo postupov štátneho overovania kandidátov. Prísny výber v prípravnej fáze prispieva k viac […]
• Bezplatné informácie prostredníctvom TIN alebo OGRN z daňového registra v celom Rusku - online Na jednotnom portáli daňových služieb, informácie o štátnej registrácii právnických osôb, fyzických osôb podnikateľov, […]
• Trest za jazdu bez dokladov (vodičský preukaz, poistka, STS) Niekedy kvôli zábudlivosti si vodiči sadnú za volant bez preukazu a dostanú pokutu za jazdu bez dokladov. Pripomeňme, že motorista jazdiaci s ním bez problémov […]
• Kvety pre mužov. Aké kvety môžete dať mužovi? Aké kvety možno dať mužovi? Nie je toľko "mužských" kvetov, ale sú také, ktoré sa dávajú mužom. Malý zoznam kvetov pred vami: Chryzantémy. ruže. Karafiáty. […]
• Memo je špeciálna forma dokumentu, ktorý sa používa v internom prostredí podniku a slúži na rýchle riešenie aktuálnych výrobných problémov. Zvyčajne je tento dokument vypracovaný na účely vytvorenia niektorých […]
• Kedy a ako získať financovanú časť dôchodku v Sberbank? Sberbank je partnerskou bankou štátneho dôchodkového fondu. Na základe toho by občania, ktorí vydali kapitalizačný dôchodok, mohli previesť financovaný […]
• Prídavky na deti v Uljanovsku a Uljanovskej oblasti v roku 2018 Okrem toho vo všetkých regiónoch fungujú programy schválené federálnym zákonom. Pozrime sa, na koho a aké výhody môže počítať. Ako regionálne orgány […]
• Podrobný návod, ako vyhotoviť splnomocnenie na zastupovanie záujmov jednotlivca na súde V občianskoprávnom alebo rozhodcovskom konaní, v správnom alebo trestnom konaní môže záujmy žalobcu aj žalovaného zastupovať advokát: […]

základné vlastnosti.

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

rovnaké dôvody

log6 4 + log6 9.

Teraz si úlohu trochu skomplikujeme.

Príklady riešenia logaritmov

Čo ak existuje stupeň v základe alebo argumente logaritmu? Potom môže byť exponent tohto stupňa vyňatý zo znamienka logaritmu podľa nasledujúcich pravidiel:

Samozrejme, všetky tieto pravidlá dávajú zmysel, ak je dodržaný logaritmus ODZ: a > 0, a ≠ 1, x >

Úloha. Nájdite hodnotu výrazu:

Prechod na nový základ

Nech je daný logaritmus logax. Potom pre akékoľvek číslo c také, že c > 0 a c ≠ 1, platí rovnosť:

Úloha. Nájdite hodnotu výrazu:

Pozri tiež:

Základné vlastnosti logaritmu

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Exponent je 2,718281828…. Aby ste si zapamätali exponent, môžete si preštudovať pravidlo: exponent je 2,7 a dvojnásobok roku narodenia Leva Tolstého.

Základné vlastnosti logaritmov

Keď poznáte toto pravidlo, budete poznať presnú hodnotu exponenta aj dátum narodenia Leva Tolstého.

Príklady pre logaritmy

Vezmite logaritmus výrazov

Príklad 1
a). x=10ac^2 (a>0, c>0).

Podľa vlastností 3,5 vypočítame

2.

3.

4. kde .

Príklad 2 Nájdite x ak

Príklad 3. Nech je uvedená hodnota logaritmov

Vypočítajte log(x), ak

Základné vlastnosti logaritmov

Logaritmy, ako každé číslo, možno sčítať, odčítať a previesť všetkými možnými spôsobmi. Ale keďže logaritmy nie sú celkom bežné čísla, existujú tu pravidlá, ktoré sa nazývajú základné vlastnosti.

Tieto pravidlá musia byť známe - bez nich nemožno vyriešiť žiadny vážny logaritmický problém. Navyše je ich veľmi málo – všetko sa dá naučiť za jeden deň. Tak poďme na to.

Sčítanie a odčítanie logaritmov

Zvážte dva logaritmy s rovnakým základom: logax a logay. Potom ich možno sčítať a odčítať a:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

Súčet logaritmov sa teda rovná logaritmu súčinu a rozdiel je logaritmus kvocientu. Poznámka: kľúčovým bodom je tu - rovnaké dôvody. Ak sú základy odlišné, tieto pravidlá nefungujú!

Tieto vzorce pomôžu vypočítať logaritmický výraz, aj keď sa neberú do úvahy jeho jednotlivé časti (pozri lekciu „Čo je logaritmus“). Pozrite sa na príklady a uvidíte:

Keďže základy logaritmov sú rovnaké, použijeme súčtový vzorec:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Úloha. Nájdite hodnotu výrazu: log2 48 − log2 3.

Základy sú rovnaké, používame rozdielový vzorec:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Úloha. Nájdite hodnotu výrazu: log3 135 − log3 5.

Opäť platí, že základy sú rovnaké, takže máme:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Ako vidíte, pôvodné výrazy sa skladajú zo „zlých“ logaritmov, ktoré sa neuvažujú samostatne. Ale po transformáciách sa ukážu celkom normálne čísla. Mnohé testy sú založené na tejto skutočnosti. Áno, kontrola – na skúške sú ponúkané podobné výrazy úplne vážne (niekedy – prakticky bez zmien).

Odstránenie exponentu z logaritmu

Je ľahké vidieť, že posledné pravidlo nasleduje ich prvé dve. Ale je lepšie si to aj tak zapamätať – v niektorých prípadoch to výrazne zníži množstvo výpočtov.

Všetky tieto pravidlá majú samozrejme zmysel, ak sa dodrží logaritmus ODZ: a > 0, a ≠ 1, x > 0. A ešte niečo: naučte sa aplikovať všetky vzorce nielen zľava doprava, ale aj naopak, t.j. môžete zadať čísla pred znamienkom logaritmu do samotného logaritmu. To je to, čo sa najčastejšie vyžaduje.

Úloha. Nájdite hodnotu výrazu: log7 496.

Zbavme sa stupňa v argumente podľa prvého vzorca:
log7 496 = 6 log7 49 = 6 2 = 12

Úloha. Nájdite hodnotu výrazu:

Všimnite si, že menovateľ je logaritmus, ktorého základ a argument sú presné mocniny: 16 = 24; 49 = 72. Máme:

Myslím, že posledný príklad potrebuje objasnenie. Kam zmizli logaritmy? Do poslednej chvíle pracujeme len s menovateľom.

Vzorce logaritmov. Logaritmy sú príklady riešení.

Predložili základ a argument tam stojaceho logaritmu vo forme stupňov a vybrali ukazovatele - dostali „trojposchodový“ zlomok.

Teraz sa pozrime na hlavný zlomok. Čitateľ a menovateľ majú rovnaké číslo: log2 7. Keďže log2 7 ≠ 0, zlomok môžeme zmenšiť - 2/4 zostanú v menovateli. Podľa pravidiel aritmetiky môžu byť štyri prenesené do čitateľa, čo sa stalo. Výsledkom je odpoveď: 2.

Prechod na nový základ

Keď už hovoríme o pravidlách sčítania a odčítania logaritmov, osobitne som zdôraznil, že fungujú iba s rovnakými základmi. Čo ak sú základy odlišné? Čo ak to nie sú presné mocniny rovnakého čísla?

Na pomoc prichádzajú vzorce pre prechod na novú základňu. Formulujeme ich vo forme vety:

Nech je daný logaritmus logax. Potom pre akékoľvek číslo c také, že c > 0 a c ≠ 1, platí rovnosť:

Konkrétne, ak dáme c = x, dostaneme:

Z druhého vzorca vyplýva, že je možné zameniť základ a argument logaritmu, ale v tomto prípade je celý výraz „prevrátený“, t.j. logaritmus je v menovateli.

Tieto vzorce sa zriedka nachádzajú v bežných číselných výrazoch. Ich vhodnosť je možné vyhodnotiť len pri riešení logaritmických rovníc a nerovníc.

Sú však úlohy, ktoré sa nedajú vyriešiť vôbec inak ako presťahovaním sa do nového základu. Uvažujme o niekoľkých z nich:

Úloha. Nájdite hodnotu výrazu: log5 16 log2 25.

Všimnite si, že argumenty oboch logaritmov sú presné exponenty. Vyberme ukazovatele: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Teraz otočme druhý logaritmus:

Keďže súčin sa nemení permutáciou faktorov, pokojne sme vynásobili štyri a dva a potom sme prišli na logaritmy.

Úloha. Nájdite hodnotu výrazu: log9 100 lg 3.

Základom a argumentom prvého logaritmu sú presné mocniny. Poďme si to zapísať a zbaviť sa indikátorov:

Teraz sa zbavme desiatkového logaritmu prechodom na nový základ:

Základná logaritmická identita

V procese riešenia je často potrebné reprezentovať číslo ako logaritmus k danej báze. V tomto prípade nám pomôžu vzorce:

V prvom prípade sa číslo n stane exponentom v argumente. Číslo n môže byť úplne čokoľvek, pretože je to len hodnota logaritmu.

Druhý vzorec je vlastne parafrázovaná definícia. Volá sa to takto:

Čo sa stane, ak sa číslo b zvýši do takej miery, že číslo b v tomto stupni dáva číslo a? Správne: toto je rovnaké číslo a. Pozorne si prečítajte tento odsek ešte raz - veľa ľudí na ňom „visí“.

Rovnako ako nové základné konverzné vzorce, základná logaritmická identita je niekedy jediným možným riešením.

Úloha. Nájdite hodnotu výrazu:

Všimnite si, že log25 64 = log5 8 - práve vytiahol štvorec zo základne a argument logaritmu. Vzhľadom na pravidlá násobenia právomocí s rovnakým základom dostaneme:

Ak niekto nevie, toto bola skutočná úloha z Jednotnej štátnej skúšky 🙂

Logaritmická jednotka a logaritmická nula

Na záver uvediem dve identity, ktoré je ťažké nazvať vlastnosťami – skôr ide o dôsledky z definície logaritmu. Neustále sa nachádzajú v problémoch a prekvapivo robia problémy aj „pokročilým“ žiakom.

1. logaa = 1 je. Pamätajte si raz a navždy: logaritmus k ľubovoľnej základni a z tejto samotnej základne sa rovná jednej.
2. loga 1 = 0 je. Základom a môže byť čokoľvek, ale ak je argument jedna, logaritmus je nula! Pretože a0 = 1 je priamym dôsledkom definície.

To sú všetky vlastnosti. Určite si ich nacvičte v praxi! Stiahnite si cheat sheet na začiatku lekcie, vytlačte si ho a vyriešte problémy.

Pozri tiež:

Logaritmus čísla b so základom a označuje výraz. Vypočítať logaritmus znamená nájsť takú mocninu x (), pri ktorej platí rovnosť

Základné vlastnosti logaritmu

Vyššie uvedené vlastnosti je potrebné poznať, pretože na ich základe sa takmer všetky problémy a príklady riešia na základe logaritmov. Zostávajúce exotické vlastnosti možno odvodiť matematickými manipuláciami s týmito vzorcami

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Pri výpočte vzorcov pre súčet a rozdiel logaritmov (3.4) sa stretávame pomerne často. Ostatné sú trochu zložité, ale v mnohých úlohách sú nevyhnutné na zjednodušenie zložitých výrazov a výpočet ich hodnôt.

Bežné prípady logaritmov

Niektoré z bežných logaritmov sú tie, v ktorých je základ dokonca desať, exponenciálny alebo dvojkový.
Logaritmus základnej desiatky sa zvyčajne nazýva logaritmus základnej desiatky a jednoducho sa označuje lg(x).

Zo záznamu je vidieť, že základy nie sú v zázname zapísané. Napríklad

Prirodzený logaritmus je logaritmus, ktorého základom je exponent (označený ln(x)).

Exponent je 2,718281828…. Aby ste si zapamätali exponent, môžete si preštudovať pravidlo: exponent je 2,7 a dvojnásobok roku narodenia Leva Tolstého. Keď poznáte toto pravidlo, budete poznať presnú hodnotu exponenta aj dátum narodenia Leva Tolstého.

A ďalší dôležitý logaritmus základne dva je

Derivácia logaritmu funkcie sa rovná jednej delenej premennou

Integrálny alebo primitívny logaritmus je určený závislosťou

Vyššie uvedený materiál je dostatočný na to, aby ste vyriešili širokú triedu problémov súvisiacich s logaritmami a logaritmami. Pre asimiláciu materiálu uvediem len niekoľko bežných príkladov zo školských osnov a univerzít.

Príklady pre logaritmy

Vezmite logaritmus výrazov

Príklad 1
a). x=10ac^2 (a>0, c>0).

Podľa vlastností 3,5 vypočítame

2.
Podľa rozdielovej vlastnosti logaritmov máme

3.
Pomocou vlastností 3.5 nájdeme

4. kde .

Zdanlivo zložitý výraz využívajúci sériu pravidiel je zjednodušený na formulár

Nájdenie hodnôt logaritmu

Príklad 2 Nájdite x ak

rozhodnutie. Pre výpočet používame vlastnosti 5 a 13 až do posledného termínu

Náhradník v zázname a smútiť

Keďže základy sú rovnaké, dávame rovnítko medzi výrazy

Logaritmy. Prvá úroveň.

Nech je uvedená hodnota logaritmov

Vypočítajte log(x), ak

Riešenie: Zoberte logaritmus premennej na zápis logaritmu cez súčet členov

Toto je len začiatok oboznámenia sa s logaritmami a ich vlastnosťami. Precvičte si výpočty, obohaťte svoje praktické zručnosti – nadobudnuté vedomosti budete čoskoro potrebovať na riešenie logaritmických rovníc. Po preštudovaní základných metód riešenia takýchto rovníc rozšírime vaše vedomosti o ďalšiu rovnako dôležitú tému - logaritmické nerovnosti ...

Základné vlastnosti logaritmov

Logaritmy, ako každé číslo, možno sčítať, odčítať a previesť všetkými možnými spôsobmi. Ale keďže logaritmy nie sú celkom bežné čísla, existujú tu pravidlá, ktoré sa nazývajú základné vlastnosti.

Tieto pravidlá musia byť známe - bez nich nemožno vyriešiť žiadny vážny logaritmický problém. Navyše je ich veľmi málo – všetko sa dá naučiť za jeden deň. Tak poďme na to.

Sčítanie a odčítanie logaritmov

Zvážte dva logaritmy s rovnakým základom: logax a logay. Potom ich možno sčítať a odčítať a:

1. logax + logay = log(x y);
2. logax − logay = log(x: y).

Súčet logaritmov sa teda rovná logaritmu súčinu a rozdiel je logaritmus kvocientu. Poznámka: kľúčovým bodom je tu - rovnaké dôvody. Ak sú základy odlišné, tieto pravidlá nefungujú!

Tieto vzorce pomôžu vypočítať logaritmický výraz, aj keď sa neberú do úvahy jeho jednotlivé časti (pozri lekciu „Čo je logaritmus“). Pozrite sa na príklady a uvidíte:

Úloha. Nájdite hodnotu výrazu: log6 4 + log6 9.

Keďže základy logaritmov sú rovnaké, použijeme súčtový vzorec:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Úloha. Nájdite hodnotu výrazu: log2 48 − log2 3.

Základy sú rovnaké, používame rozdielový vzorec:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Úloha. Nájdite hodnotu výrazu: log3 135 − log3 5.

Opäť platí, že základy sú rovnaké, takže máme:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Ako vidíte, pôvodné výrazy sa skladajú zo „zlých“ logaritmov, ktoré sa neuvažujú samostatne. Ale po transformáciách sa ukážu celkom normálne čísla. Mnohé testy sú založené na tejto skutočnosti. Áno, kontrola – na skúške sú ponúkané podobné výrazy úplne vážne (niekedy – prakticky bez zmien).

Odstránenie exponentu z logaritmu

Teraz si úlohu trochu skomplikujeme. Čo ak existuje stupeň v základe alebo argumente logaritmu? Potom môže byť exponent tohto stupňa vyňatý zo znamienka logaritmu podľa nasledujúcich pravidiel:

Je ľahké vidieť, že posledné pravidlo nasleduje ich prvé dve. Ale je lepšie si to aj tak zapamätať – v niektorých prípadoch to výrazne zníži množstvo výpočtov.

Všetky tieto pravidlá majú samozrejme zmysel, ak sa dodrží logaritmus ODZ: a > 0, a ≠ 1, x > 0. A ešte niečo: naučte sa aplikovať všetky vzorce nielen zľava doprava, ale aj naopak, t.j. môžete zadať čísla pred znamienkom logaritmu do samotného logaritmu.

Ako riešiť logaritmy

To je to, čo sa najčastejšie vyžaduje.

Úloha. Nájdite hodnotu výrazu: log7 496.

Zbavme sa stupňa v argumente podľa prvého vzorca:
log7 496 = 6 log7 49 = 6 2 = 12

Úloha. Nájdite hodnotu výrazu:

Všimnite si, že menovateľ je logaritmus, ktorého základ a argument sú presné mocniny: 16 = 24; 49 = 72. Máme:

Myslím, že posledný príklad potrebuje objasnenie. Kam zmizli logaritmy? Do poslednej chvíle pracujeme len s menovateľom. Predložili základ a argument tam stojaceho logaritmu vo forme stupňov a vybrali ukazovatele - dostali „trojposchodový“ zlomok.

Teraz sa pozrime na hlavný zlomok. Čitateľ a menovateľ majú rovnaké číslo: log2 7. Keďže log2 7 ≠ 0, zlomok môžeme zmenšiť - 2/4 zostanú v menovateli. Podľa pravidiel aritmetiky môžu byť štyri prenesené do čitateľa, čo sa stalo. Výsledkom je odpoveď: 2.

Prechod na nový základ

Keď už hovoríme o pravidlách sčítania a odčítania logaritmov, osobitne som zdôraznil, že fungujú iba s rovnakými základmi. Čo ak sú základy odlišné? Čo ak to nie sú presné mocniny rovnakého čísla?

Na pomoc prichádzajú vzorce pre prechod na novú základňu. Formulujeme ich vo forme vety:

Nech je daný logaritmus logax. Potom pre akékoľvek číslo c také, že c > 0 a c ≠ 1, platí rovnosť:

Konkrétne, ak dáme c = x, dostaneme:

Z druhého vzorca vyplýva, že je možné zameniť základ a argument logaritmu, ale v tomto prípade je celý výraz „prevrátený“, t.j. logaritmus je v menovateli.

Tieto vzorce sa zriedka nachádzajú v bežných číselných výrazoch. Ich vhodnosť je možné vyhodnotiť len pri riešení logaritmických rovníc a nerovníc.

Sú však úlohy, ktoré sa nedajú vyriešiť vôbec inak ako presťahovaním sa do nového základu. Uvažujme o niekoľkých z nich:

Úloha. Nájdite hodnotu výrazu: log5 16 log2 25.

Všimnite si, že argumenty oboch logaritmov sú presné exponenty. Vyberme ukazovatele: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Teraz otočme druhý logaritmus:

Keďže súčin sa nemení permutáciou faktorov, pokojne sme vynásobili štyri a dva a potom sme prišli na logaritmy.

Úloha. Nájdite hodnotu výrazu: log9 100 lg 3.

Základom a argumentom prvého logaritmu sú presné mocniny. Poďme si to zapísať a zbaviť sa indikátorov:

Teraz sa zbavme desiatkového logaritmu prechodom na nový základ:

Základná logaritmická identita

V procese riešenia je často potrebné reprezentovať číslo ako logaritmus k danej báze. V tomto prípade nám pomôžu vzorce:

V prvom prípade sa číslo n stane exponentom v argumente. Číslo n môže byť úplne čokoľvek, pretože je to len hodnota logaritmu.

Druhý vzorec je vlastne parafrázovaná definícia. Volá sa to takto:

Čo sa stane, ak sa číslo b zvýši do takej miery, že číslo b v tomto stupni dáva číslo a? Správne: toto je rovnaké číslo a. Pozorne si prečítajte tento odsek ešte raz - veľa ľudí na ňom „visí“.

Rovnako ako nové základné konverzné vzorce, základná logaritmická identita je niekedy jediným možným riešením.

Úloha. Nájdite hodnotu výrazu:

Všimnite si, že log25 64 = log5 8 - práve vytiahol štvorec zo základne a argument logaritmu. Vzhľadom na pravidlá násobenia právomocí s rovnakým základom dostaneme:

Ak niekto nevie, toto bola skutočná úloha z Jednotnej štátnej skúšky 🙂

Logaritmická jednotka a logaritmická nula

Na záver uvediem dve identity, ktoré je ťažké nazvať vlastnosťami – skôr ide o dôsledky z definície logaritmu. Neustále sa nachádzajú v problémoch a prekvapivo robia problémy aj „pokročilým“ žiakom.

1. logaa = 1 je. Pamätajte si raz a navždy: logaritmus k ľubovoľnej základni a z tejto samotnej základne sa rovná jednej.
2. loga 1 = 0 je. Základom a môže byť čokoľvek, ale ak je argument jedna, logaritmus je nula! Pretože a0 = 1 je priamym dôsledkom definície.

To sú všetky vlastnosti. Určite si ich nacvičte v praxi! Stiahnite si cheat sheet na začiatku lekcie, vytlačte si ho a vyriešte problémy.