Tangens jest linią prostą przechodzącą przez punkt krzywej i pokrywającą się z nim w tym punkcie aż do pierwszego rzędu (ryc. 1).

Inna definicja: to jest położenie graniczne siecznej w Δ X→0.

Wyjaśnienie: Weźmy linię przecinającą krzywą w dwóch punktach: A I B(widzieć zdjęcie). To jest sieczna. Będziemy go obracać zgodnie z ruchem wskazówek zegara, aż będzie miał tylko jeden wspólny punkt z krzywą. Otrzymujemy więc styczną.

Ścisła definicja stycznej:

Styczna do wykresu funkcji F, różniczkowalna w punkcie XO, to linia przechodząca przez punkt ( XO; F(XO)) i mający nachylenie F′( XO).

Zbocze ma linię prostą y=kx +B. Współczynnik k i jest współczynnik nachylenia ta prosta linia.

Współczynnik kątowy jest równy tangensowi kąta ostrego utworzonego przez tę prostą z osią x:

k = tgα

Tutaj kąt α jest kątem między prostą y=kx +B oraz dodatni (tj. przeciwnie do ruchu wskazówek zegara) kierunek osi x. Nazywa się to kąt nachylenia prosty(Rys. 1 i 2).

Jeśli kąt nachylenia jest prosty y=kx +B ostre, to nachylenie jest liczbą dodatnią. Wykres rośnie (ryc. 1).

Jeśli kąt nachylenia jest prosty y=kx +B rozwarty, to nachylenie jest liczbą ujemną. Wykres maleje (ryc. 2).

Jeśli linia jest równoległa do osi x, to nachylenie linii wynosi zero. W tym przypadku nachylenie linii również wynosi zero (ponieważ tangens zera wynosi zero). Równanie linii prostej będzie wyglądać następująco: y = b (ryc. 3).

Jeśli kąt nachylenia prostej wynosi 90º (π/2), czyli jest prostopadła do osi x, to prosta jest dana przez równość x=C, Gdzie C- pewna liczba rzeczywista (ryc. 4).

Równanie stycznej do wykresu funkcjiy = F(X) w punkcie XO:

Przykład: Znajdźmy równanie stycznej do wykresu funkcji F(X) = X 3 – 2X 2 + 1 w punkcie z odciętymi 2.

Rozwiązanie .

Postępujemy zgodnie z algorytmem.

1) Punkt dotykowy XO równa się 2. Oblicz F(XO):

F(XO) = F(2) = 2 3 – 2 ∙ 2 2 + 1 = 8 – 8 + 1 = 1

2) Znajdź F′( X). Aby to zrobić, używamy wzorów różniczkowania przedstawionych w poprzedniej sekcji. Według tych formuł, X 2 = 2X, A X 3 = 3X 2. Oznacza:

F′( X) = 3X 2 – 2 ∙ 2X = 3X 2 – 4X.

Teraz, używając wynikowej wartości F′( X), Oblicz F′( XO):

F′( XO) = F′(2) = 3 ∙ 2 2 – 4 ∙ 2 = 12 – 8 = 4.

3) Mamy więc wszystkie niezbędne dane: XO = 2, F(XO) = 1, F ′( XO) = 4. Podstawiamy te liczby do równania stycznego i znajdujemy końcowe rozwiązanie:

y= F(XO) + F′( XO) (x – x o) \u003d 1 + 4 ∙ (x - 2) \u003d 1 + 4x - 8 \u003d -7 + 4x \u003d 4x - 7.

Odpowiedź: y \u003d 4x - 7.

Artykuł zawiera szczegółowe wyjaśnienie definicji, geometryczne znaczenie pochodnej z notacją graficzną. Równanie linii stycznej zostanie rozważone z przykładami, zostaną znalezione równania stycznej do krzywych drugiego rzędu.

Yandex.RTB R-A-339285-1 Definicja 1

Kąt nachylenia linii prostej y \u003d k x + b nazywany jest kątem α, który jest mierzony od dodatniego kierunku osi x do prostej y \u003d k x + b w kierunku dodatnim.

Na rysunku kierunek ox jest oznaczony zieloną strzałką i zielonym łukiem, a kąt nachylenia czerwonym łukiem. Niebieska linia odnosi się do linii prostej.

Definicja 2

Nachylenie linii prostej y \u003d k x + b nazywa się współczynnikiem liczbowym k.

Nachylenie jest równe nachyleniu linii prostej, innymi słowy k = t g α .

• Nachylenie prostej wynosi 0 tylko wtedy, gdy o x jest równoległe i nachylenie jest równe zeru, ponieważ tangens zera wynosi 0. Tak więc postać równania będzie miała postać y = b.
• Jeżeli kąt nachylenia linii prostej y = k x + b jest ostry, to warunki 0< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 , a na wykresie jest wzrost.
• Jeśli α \u003d π 2, to położenie linii jest prostopadłe do x. Równość jest określona przez równość x = c, gdzie wartość c jest liczbą rzeczywistą.
• Jeżeli kąt nachylenia linii prostej y = k x + b jest rozwarty, to odpowiada warunkom π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Definicja 3

Sieczna to prosta przechodząca przez 2 punkty funkcji f(x). Innymi słowy, sieczna jest linią prostą przechodzącą przez dowolne dwa punkty na wykresie danej funkcji.

Rysunek pokazuje, że AB jest sieczną, a f (x) jest czarną krzywą, α jest czerwonym łukiem, wskazującym kąt nachylenia siecznej.

Kiedy nachylenie prostej jest równe tangensowi kąta nachylenia, jasne jest, że styczną z trójkąta prostokątnego A B C można znaleźć w stosunku do przeciwległej nogi do sąsiedniej.

Definicja 4

Otrzymujemy wzór na znalezienie siecznej formy:

k = t g α = B C A C = f (x B) - f x A x B - x A , gdzie odcięte punktów A i B są wartościami x A , x B , i f (x A) , f (x B) to wartości funkcji w tych punktach.

Oczywiście nachylenie siecznej jest określone za pomocą równości k \u003d f (x B) - f (x A) x B - x A lub k \u003d f (x A) - f (x B) x A - x B, a równanie należy zapisać jako y = f (x B) - f (x A) x B - x A x - x A + f (x A) lub
y = fa (x ZA) - fa (x b) x ZA - x b x - x b + fa (x b) .

Sieczna wizualnie dzieli wykres na 3 części: na lewo od punktu A, od A do B, na prawo od B. Poniższy rysunek pokazuje, że istnieją trzy sieczne, które są uważane za takie same, to znaczy są ustawić za pomocą podobnego równania.

Z definicji jasne jest, że prosta i jej sieczna pokrywają się w tym przypadku.

Sieczna może wielokrotnie przecinać wykres danej funkcji. Jeśli istnieje równanie postaci y \u003d 0 dla siecznej, to liczba punktów przecięcia z sinusoidą jest nieskończona.

Definicja 5

Styczna do wykresu funkcji f(x) w punkcie x 0 ; f (x 0) nazywamy linią prostą przechodzącą przez dany punkt x 0; f (x 0) , z obecnością segmentu, który ma wiele wartości x bliskich x 0 .

Przykład 1

Przyjrzyjmy się bliżej poniższemu przykładowi. Wtedy widać, że prosta dana przez funkcję y = x + 1 jest uważana za styczną do y = 2 x w punkcie o współrzędnych (1 ; 2) . Dla jasności konieczne jest rozważenie wykresów o wartościach bliskich (1; 2). Funkcja y = 2 x jest zaznaczona na czarno, niebieska linia to styczna, czerwona kropka to punkt przecięcia.

Oczywiście y \u003d 2 x łączy się z linią y \u003d x + 1.

Aby wyznaczyć styczną, należy rozważyć zachowanie się stycznej A B, gdy punkt B zbliża się w nieskończoność do punktu A. Dla jasności przedstawiamy rysunek.

Sieczna AB, oznaczona niebieską linią, dąży do położenia samej stycznej, a kąt nachylenia siecznej α zacznie zbliżać się do kąta nachylenia samej stycznej α x.

Definicja 6

Styczna do wykresu funkcji y \u003d f (x) w punkcie A jest granicznym położeniem siecznej AB w B zmierzającej do A, to znaczy B → A.

Przejdźmy teraz do rozważenia geometrycznego znaczenia pochodnej funkcji w punkcie.

Przejdźmy do rozważenia siecznej A B dla funkcji f (x), gdzie A i B o współrzędnych x 0, f (x 0) i x 0 + ∆ x, f (x 0 + ∆ x) i ∆ x jest oznaczane jako przyrost argumentu. Teraz funkcja przyjmie postać ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . Dla jasności zróbmy zdjęcie jako przykład.

Rozważmy wynikowy trójkąt prostokątny A B C. Korzystamy z definicji tangensa dla rozwiązania, czyli otrzymujemy stosunek ∆ y ∆ x = t g α . Z definicji stycznej wynika, że ​​lim ∆ x → 0 ∆ y ∆ x = t g α x . Zgodnie z regułą pochodnej w punkcie mamy, że pochodna f(x) w punkcie x 0 nazywana jest granicą stosunku przyrostu funkcji do przyrostu argumentu, gdzie ∆ x → 0, to oznaczone jako f (x 0) = lim ∆ x → 0 ∆ y ∆ x .

Wynika z tego, że f "(x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, gdzie k x oznaczamy jako nachylenie stycznej.

Czyli otrzymujemy, że f ' (x) może istnieć w punkcie x 0 i oprócz stycznej do danego wykresu funkcji w punkcie styku równym x 0 , f 0 (x 0) , gdzie wartość nachylenia stycznej w punkcie jest równa pochodnej w punkcie x 0 . Wtedy otrzymujemy, że k x = f "(x 0) .

Geometryczne znaczenie pochodnej funkcji w punkcie polega na tym, że dana jest koncepcja istnienia stycznej do wykresu w tym samym punkcie.

Aby napisać równanie dowolnej linii prostej na płaszczyźnie, konieczne jest posiadanie nachylenia z punktem, przez który przechodzi. Jego oznaczenie przyjmuje się jako x 0 na przecięciu.

Równanie stycznej do wykresu funkcji y \u003d f (x) w punkcie x 0, f 0 (x 0) ma postać y \u003d f "(x 0) x - x 0 + f (x 0) .

Oznacza to, że końcowa wartość pochodnej f "(x 0) może określić położenie stycznej, czyli w pionie pod warunkiem lim x → x 0 + 0 f" (x) = ∞ i lim x → x 0 - 0 fa "(x ) = ∞ lub brak w ogóle pod warunkiem lim x → x 0 + 0 fa "(x) ≠ lim x → x 0 - 0 fa "(x) .

Położenie stycznej zależy od wartości jej nachylenia k x \u003d f "(x 0). Gdy równolegle do osi x, otrzymujemy to k k \u003d 0, gdy równolegle do około y - k x \u003d ∞, a postać równania stycznego x \u003d x 0 rośnie wraz z k x > 0 , maleje, gdy k x< 0 .

Przykład 2

Skompiluj równanie stycznej do wykresu funkcji y \u003d mi x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 w punkcie o współrzędnych (1; 3) z definicją kąta nachylenie.

Rozwiązanie

Z założenia mamy, że funkcja jest zdefiniowana dla wszystkich liczb rzeczywistych. Otrzymujemy, że punkt o współrzędnych określonych przez warunek (1 ; 3) jest punktem styku, wtedy x 0 = - 1 , f (x 0) = - 3 .

Należy znaleźć pochodną w punkcie o wartości -1 . Rozumiemy to

y "= mi x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3" = = mi x + 1 "+ x 3 3" - 6 - 3 3 x "- 17 - 3 3" = mi x + 1 + x 2 - 6 - 3 3 y "(x 0) = y" (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

Wartość f’ (x) w punkcie styku jest nachyleniem stycznej, która jest równa stycznej nachylenia.

Wtedy k x = t g α x = y "(x 0) = 3 3

Wynika z tego, że α x = a r c t g 3 3 = π 6

Odpowiedź: równanie styczne przyjmuje postać

y \u003d f "(x 0) x - x 0 + fa (x 0) y \u003d 3 3 (x + 1) - 3 y \u003d 3 3 x - 9 - 3 3

Dla jasności podajemy przykład na ilustracji graficznej.

Czarny kolor jest używany do wykresu oryginalnej funkcji, niebieski kolor to obraz styczny, czerwona kropka to punkt styku. Rysunek po prawej stronie przedstawia widok w powiększeniu.

Przykład 3

Znajdź istnienie stycznej do wykresu danej funkcji
y = 3 x - 1 5 + 1 w punkcie o współrzędnych (1 ; 1) . Napisz równanie i wyznacz kąt nachylenia.

Rozwiązanie

Z założenia mamy, że dziedziną danej funkcji jest zbiór wszystkich liczb rzeczywistych.

Przejdźmy do szukania pochodnej

y "= 3 x - 1 5 + 1" = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Jeśli x 0 = 1 , to f ' (x) nie jest zdefiniowane, ale granice są zapisane jako lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 1 + 0 = + ∞ i lim x → 1 - 0 3 5 1 (x - 1) 4 5 = 3 5 1 (- 0) 4 5 = 3 5 1 + 0 = + ∞ , co oznacza istnienie stycznej pionowej w punkt (1 ; 1) .

Odpowiedź: równanie przyjmie postać x \u003d 1, gdzie kąt nachylenia będzie równy π 2.

Narysujmy to dla jasności.

Przykład 4

Znajdź punkty wykresu funkcji y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 , gdzie

1. Styczna nie istnieje;
2. Styczna jest równoległa do x;
3. Styczna jest równoległa do prostej y = 8 5 x + 4 .

Rozwiązanie

Konieczne jest zwrócenie uwagi na dziedzinę definicji. Z założenia mamy, że funkcja jest zdefiniowana na zbiorze wszystkich liczb rzeczywistych. Rozwiń moduł i rozwiąż układ z przedziałami x ∈ - ∞ ; 2 i [ - 2 ; +∞) . Rozumiemy to

y = - 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; +∞)

Funkcja musi być zróżnicowana. Mamy to

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 " , x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; +∞)

Gdy x = - 2, to pochodna nie istnieje, ponieważ granice jednostronne nie są równe w tym punkcie:

limit x → - 2 - 0 y "(x) = limit x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y "(x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Obliczamy wartość funkcji w punkcie x \u003d - 2, gdzie to otrzymujemy

1. y (- 2) \u003d 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 \u003d - 2, czyli styczna w punkt (- 2; - 2) nie będzie istniał.
2. Styczna jest równoległa do x, gdy nachylenie wynosi zero. Wtedy k x \u003d t g α x \u003d f "(x 0). Oznacza to, że konieczne jest znalezienie wartości takiego x, gdy pochodna funkcji zwróci ją do zera. To znaczy wartości \u200b\u200bz f ' (x) i będą punktami styku, gdzie styczna jest równoległa do x .

Kiedy x ∈ - ∞ ; - 2 , wtedy - 1 5 (x 2 + 12 x + 35) = 0 , a dla x ∈ (- 2 ; + ∞) otrzymujemy 1 5 (x 2 - 4 x + 3) = 0 .

1 5 (x 2 + 12 x + 35) = 0 re = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 re = 4 2 - 4 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞

Obliczamy odpowiednie wartości funkcji

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Stąd - 5; 8 5 , - 4 ; 4 3, 1; 85, 3; 4 3 są uważane za pożądane punkty wykresu funkcji.

Rozważ graficzną reprezentację rozwiązania.

Czarna linia to wykres funkcji, czerwone kropki to punkty styku.

1. Gdy linie są równoległe, współczynniki kierunkowe są równe. Następnie należy szukać punktów wykresu funkcji, w których nachylenie będzie równe wartości 8 5 . Aby to zrobić, musisz rozwiązać równanie postaci y "(x) = 8 5. Następnie, jeśli x ∈ - ∞; - 2, otrzymamy to - 1 5 (x 2 + 12 x + 35) = 8 5, a jeśli x ∈ ( - 2 ; + ∞) , to 1 5 (x 2 - 4 x + 3) = 8 5 .

Pierwsze równanie nie ma pierwiastków, ponieważ wyróżnik jest mniejszy od zera. Zapiszmy to

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 R = 12 2 - 4 43 = - 28< 0

Zatem inne równanie ma dwa pierwiastki rzeczywiste

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 re = 4 2 - 4 (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞

Przejdźmy do znalezienia wartości funkcji. Rozumiemy to

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Punkty o wartościach - 1 ; 4 15, 5; 8 3 to punkty, w których styczne są równoległe do linii y = 8 5 x + 4 .

Odpowiedź: czarna linia - wykres funkcji, czerwona linia - wykres y \u003d 8 5 x + 4, niebieska linia - styczne w punktach - 1; 4 15, 5; 8 3 .

Możliwe jest istnienie nieskończonej liczby stycznych dla danych funkcji.

Przykład 5

Napisz równania wszystkich dostępnych stycznych funkcji y = 3 cos 3 2 x - π 4 - 1 3 , które są prostopadłe do prostej y = - 2 x + 1 2 .

Rozwiązanie

Aby sporządzić równanie styczne, należy znaleźć współczynnik i współrzędne punktu styku na podstawie warunku prostopadłości prostych. Definicja brzmi tak: iloczyn współczynników kierunkowych prostopadłych do prostych jest równy - 1, czyli jest zapisywany jako k x · k ⊥ = - 1. Z warunku mamy, że nachylenie jest prostopadłe do prostej i jest równe k ⊥ = - 2, wtedy k x = - 1 k ⊥ = - 1 - 2 = 1 2 .

Teraz musimy znaleźć współrzędne punktów styku. Musisz znaleźć x, po czym jego wartość dla danej funkcji. Zauważ, że z geometrycznego znaczenia pochodnej w punkcie
x 0 otrzymujemy to k x \u003d y "(x 0) . Z tej równości znajdujemy wartości x dla punktów styku.

Rozumiemy to

y "(x 0) = 3 sałata 3 2 x 0 - π 4 - 1 3" = 3 - grzech 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 grzech 3 2 x 0 - π 4 3 2 \u003d - 9 2 grzech 3 2 x 0 - π 4 ⇒ k x \u003d y "(x 0) ⇔ - 9 2 grzech 3 2 x 0 - π 4 \u003d 1 2 ⇒ grzech 3 2 x 0 - π 4 = - 1 9

To równanie trygonometryczne zostanie użyte do obliczenia rzędnych punktów styku.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk lub 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk lub 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r do grzech 1 9 + 2 πk lub x 0 = 2 3 5 π 4 + a r do grzech 1 9 + 2 πk , k ∈ Z

Z jest zbiorem liczb całkowitych.

Znaleziono x punktów kontaktowych. Teraz musisz przejść do wyszukiwania wartości y:

y 0 = 3 sałata 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - grzech 2 3 2 x 0 - π 4 - 1 3 lub y 0 = 3 - 1 - grzech 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 lub y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 lub y 0 = - 4 5 + 1 3

Stąd otrzymujemy, że 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + łuk do grzech 1 9 + 2 πk ; - 4 5 + 1 3 to punkty styku.

Odpowiedź: niezbędne równania zostaną zapisane jako

y = 1 2 x - 2 3 π 4 - a r do grzech 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r do grzech 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Aby uzyskać wizualną reprezentację, rozważ funkcję i styczną na linii współrzędnych.

Rysunek pokazuje, że położenie funkcji znajduje się w przedziale [-10; 10 ] , gdzie czarna linia to wykres funkcji, niebieskie linie to styczne prostopadłe do danej prostej postaci y = - 2 x + 1 2 . Czerwone kropki to punkty dotykowe.

Równania kanoniczne krzywych drugiego rzędu nie są funkcjami jednowartościowymi. Równania styczne dla nich są zestawiane zgodnie ze znanymi schematami.

Styczna do okręgu

Aby ustawić okrąg wyśrodkowany w punkcie x c ​​en t e r ; y c e n t e r i promień R, stosuje się wzór x - x c e n t e r 2 + y - y c e n t e r 2 = R 2.

Równość tę można zapisać jako sumę dwóch funkcji:

y = R 2 - x - x do mi n t mi r 2 + y c mi n t mi r y = - R 2 - x - x do mi n t mi r 2 + y c mi n t mi r

Pierwsza funkcja znajduje się na górze, a druga na dole, jak pokazano na rysunku.

Sporządzić równanie okręgu w punkcie x 0 ; y 0 , który znajduje się w górnym lub dolnym półkolu, powinieneś znaleźć równanie wykresu funkcji postaci y \u003d R 2 - x - x c e n t e r 2 + y c e n t e r lub y \u003d - R 2 - x - x c e n t e r 2 + y c e n t e r we wskazanym punkcie.

Kiedy w punktach x c en t e r ; y c e n t e r + R i x c e n t e r ; y c e n t e r - R tangensy można podać równaniami y = y c e n t e r + R i y = y c e n t e r - R , oraz w punktach x c e n t e r + R ; y c e n t e r i
x c e n t e r - R; y c e n t e r będzie równoległe do y, to otrzymamy równania postaci x = x c e n t e r + R i x = x c e n t e r - R .

Styczna do elipsy

Kiedy elipsa jest wyśrodkowana w x c en t e r ; y c e n t e r z półosiami a i b , to można go podać za pomocą równania x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 .

Elipsę i okrąg można oznaczyć, łącząc dwie funkcje, a mianowicie górną i dolną półelipsę. Wtedy to rozumiemy

y = b za a 2 - (x - x c mi n t mi r) 2 + y c mi n t e r y = - b za a 2 - (x - x c mi n t mi r) 2 + y c mi n t mi r

Jeśli styczne znajdują się w wierzchołkach elipsy, to są równoległe względem x lub względem y. Dla jasności rozważ poniższy rysunek.

Przykład 6

Napisz równanie stycznej do elipsy x - 3 2 4 + y - 5 2 25 = 1 w punktach o wartościach x równych x = 2 .

Rozwiązanie

Konieczne jest znalezienie punktów styku, które odpowiadają wartości x = 2. Dokonujemy podstawienia do istniejącego równania elipsy i otrzymujemy to

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

następnie 2; 5 3 2 + 5 i 2 ; - 5 3 2 + 5 to punkty styczne należące do górnej i dolnej półelipsy.

Przejdźmy do znajdowania i rozwiązywania równania elipsy względem y. Rozumiemy to

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Jest oczywiste, że górna półelipsa jest określona funkcją postaci y = 5 + 5 2 4 - x - 3 2 , a dolna y = 5 - 5 2 4 - x - 3 2 .

Stosujemy standardowy algorytm w celu sformułowania równania stycznej do wykresu funkcji w punkcie. Piszemy, że równanie dla pierwszej stycznej w punkcie 2 ; 5 3 2 + 5 będzie wyglądać

y "= 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y "(x 0) = y" (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

Otrzymujemy równanie drugiej stycznej z wartością w punkcie
2; - 5 3 2 + 5 staje się

y "= 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y "(x 0) = y" (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y "(x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Graficznie styczne są oznaczone w następujący sposób:

Styczna do hiperboli

Kiedy hiperbola ma środek w punkcie x c ​​en t e r ; y c e n t e r i wierzchołki x c e n t e r + α ; y c e n t e r i x c e n t e r - α; y c e n t e r , nierówność x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1 jest dana jeśli z wierzchołkami x c e n t e r ; y c e n t e r + b i x c e n t mi r ; y c e n t e r - b jest wtedy dane przez nierówność x - x c e n t e r 2 α 2 - y - y c e n t mi r 2 b 2 = - 1 .

Hiperbolę można przedstawić jako dwie połączone funkcje formy

y = b za (x - x c mi n t e r) 2 - za 2 + y c mi n t e r y = - b za (x - x c mi n t e r) 2 - a 2 + y c mi n t e r lub y = b a (x - x c mi n t mi r) 2 + za 2 + y c mi n t e r y = - b za (x - x c mi n t e r ) 2 + za 2 + y c e n t e r

W pierwszym przypadku mamy, że styczne są równoległe do y, aw drugim są równoległe do x.

Wynika z tego, że aby znaleźć równanie stycznej do hiperboli, należy dowiedzieć się, do której funkcji należy punkt styczny. Aby to ustalić, konieczne jest dokonanie podstawienia w równaniach i sprawdzenie ich tożsamości.

Przykład 7

Zapisz równanie stycznej do hiperboli x - 3 2 4 - y + 3 2 9 = 1 w punkcie 7; - 3 3 - 3 .

Rozwiązanie

Konieczne jest przekształcenie zapisu rozwiązania znalezienia hiperboli za pomocą 2 funkcji. Rozumiemy to

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 lub y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Należy dowiedzieć się, do jakiej funkcji należy dany punkt o współrzędnych 7; - 3 3 - 3 .

Oczywiście, aby sprawdzić pierwszą funkcję, potrzebujesz y (7) = 3 2 (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 , wtedy punkt nie należy do wykresu, ponieważ równość nie jest spełniona.

Dla drugiej funkcji mamy, że y (7) = - 3 2 (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 , co oznacza, że ​​punkt należy do danego wykresu. Stąd powinieneś znaleźć współczynnik nachylenia.

Rozumiemy to

y "= - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y "(x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Odpowiedź: równanie styczne można przedstawić jako

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Jest to wizualizowane w następujący sposób:

Styczna do paraboli

Aby ułożyć równanie stycznej do paraboli y \u003d a x 2 + b x + c w punkcie x 0, y (x 0) , musisz użyć standardowego algorytmu, wtedy równanie przyjmie postać y \u003d y " (x 0) x - x 0 + y ( x 0) Taka styczna w wierzchołku jest równoległa do x.

Parabolę x = a y 2 + b y + c należy zdefiniować jako sumę dwóch funkcji. Dlatego musimy rozwiązać równanie dla y. Rozumiemy to

x = za y 2 + b y + do ⇔ za y 2 + b y + do - x = 0 re = b 2 - 4 za (c - x) y = - b + b 2 - 4 za (c - x) 2 za y = - b - b 2 - 4 za (c - x) 2 za

Narysujmy to jako:

Aby dowiedzieć się, czy punkt x 0 , y (x 0) należy do funkcji, delikatnie postępuj zgodnie ze standardowym algorytmem. Taka styczna będzie równoległa do y względem paraboli.

Przykład 8

Napisz równanie stycznej do wykresu x - 2 y 2 - 5 y + 3, gdy mamy styczne nachylenie 150 °.

Rozwiązanie

Rozpoczynamy rozwiązanie od przedstawienia paraboli jako dwóch funkcji. Rozumiemy to

2 y 2 - 5 y + 3 - x = 0 re = (- 5) 2 - 4 (- 2) (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Wartość nachylenia jest równa wartości pochodnej w punkcie x 0 tej funkcji i jest równa tangensowi nachylenia.

Otrzymujemy:

k x \u003d y "(x 0) \u003d t g α x \u003d t g 150 ° \u003d - 1 3

Stąd określamy wartość x dla punktów styku.

Pierwsza funkcja zostanie zapisana jako

y "= 5 + 49 - 8 x - 4" = 1 49 - 8 x ⇒ y "(x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Oczywiście nie ma prawdziwych pierwiastków, ponieważ otrzymaliśmy wartość ujemną. Dochodzimy do wniosku, że dla takiej funkcji nie ma stycznej o kącie 150 °.

Druga funkcja zostanie zapisana jako

y "= 5 - 49 - 8 x - 4" = - 1 49 - 8 x ⇒ y "(x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Mamy to punkty styku - 23 4 ; - 5 + 3 4 .

Odpowiedź: równanie styczne przyjmuje postać

y = - 1 3 x - 23 4 + - 5 + 3 4

Narysujmy to tak:

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Równanie stycznej do wykresu funkcji

P. Romanow, T. Romanowa,
Magnitogorsk,
Obwód czelabiński

Równanie stycznej do wykresu funkcji

Artykuł ukazał się przy wsparciu Zespołu Hotelowego ITAKA+. Przebywając w mieście stoczniowców Siewierodwińsk, nie napotkasz problemu ze znalezieniem tymczasowego mieszkania. , na stronie internetowej kompleksu hotelowego „ITAKA +” http://itakaplus.ru możesz łatwo i szybko wynająć mieszkanie w mieście na dowolny okres, z codzienną opłatą.

Na obecnym etapie rozwoju edukacji jednym z jej głównych zadań jest kształtowanie osobowości myślącej twórczo. Zdolność do kreatywności studentów można rozwijać tylko wtedy, gdy systematycznie angażują się w podstawy działalności badawczej. Fundamentem umożliwiającym studentom wykorzystanie ich sił twórczych, zdolności i talentów jest tworzona pełnoprawna wiedza i umiejętności. W związku z tym nie bez znaczenia jest problem kształtowania systemu podstawowej wiedzy i umiejętności dla każdego tematu szkolnego kursu matematyki. Jednocześnie pełnowartościowe umiejętności powinny być celem dydaktycznym nie poszczególnych zadań, ale ich starannie przemyślanego systemu. W najszerszym znaczeniu system jest rozumiany jako zbiór powiązanych ze sobą oddziałujących na siebie elementów, który ma integralność i stabilną strukturę.

Rozważ metodologię nauczania uczniów, jak sporządzić równanie stycznej do wykresu funkcji. W istocie wszystkie zadania znalezienia równania stycznego sprowadzają się do konieczności wybrania ze zbioru (snopa, rodziny) linii tych, które spełniają określone wymaganie - są styczne do wykresu określonej funkcji. W takim przypadku zestaw linii, z którego dokonywana jest selekcja, można określić na dwa sposoby:

a) punkt leżący na płaszczyźnie xOy (środkowy ołówek linii);
b) współczynnik kątowy (równoległa wiązka linii).

W związku z tym, studiując temat „Styczna do wykresu funkcji” w celu wyodrębnienia elementów systemu, zidentyfikowaliśmy dwa rodzaje zadań:

1) zadania na stycznej określonej przez punkt, przez który ona przechodzi;
2) zadania na stycznej określonej przez jej nachylenie.

Nauka rozwiązywania problemów na stycznej została przeprowadzona przy użyciu algorytmu zaproponowanego przez A.G. Mordkowicz. Jego zasadnicza różnica w stosunku do już znanych polega na tym, że odcięta punktu stycznego jest oznaczona literą a (zamiast x0), w związku z czym równanie styczne przyjmuje postać

y \u003d fa (a) + f "(a) (x - a)

(porównaj z y \u003d f (x 0) + f "(x 0) (x - x 0)). Naszym zdaniem ta technika metodologiczna pozwala uczniom szybko i łatwo zorientować się, gdzie zapisywane są współrzędne bieżącego punktu w ogólnym równaniu stycznym i gdzie są punkty styku.

Algorytm zestawiania równania stycznej do wykresu funkcji y = f(x)

1. Oznacz literą a odcięty punkt styku.
2. Znajdź f(a).
3. Znajdź f "(x) i f "(a).
4. Zastąp znalezione liczby a, f (a), f "(a) do ogólnego równania stycznej y \u003d f (a) \u003d f "(a) (x - a).

Algorytm ten można skompilować na podstawie samodzielnego wyboru przez studentów operacji i kolejności ich wykonania.

Praktyka pokazała, że ​​​​konsekwentne rozwiązanie każdego z kluczowych zadań za pomocą algorytmu pozwala wykształcić umiejętność pisania równania stycznej do wykresu funkcji etapami, a kroki algorytmu służą jako mocne punkty do działań . Podejście to koresponduje z teorią stopniowego kształtowania się działań umysłowych opracowaną przez P.Ya. Galperin i N.F. Talyzina.

W pierwszym typie zadań zidentyfikowano dwa kluczowe zadania:

• styczna przechodzi przez punkt leżący na krzywej (zadanie 1);
• styczna przechodzi przez punkt, który nie leży na krzywej (Zadanie 2).

Zadanie 1. Przyrównaj styczną do wykresu funkcji w punkcie M(3; – 2).

Rozwiązanie. Punkt M(3; – 2) jest punktem styku, ponieważ

1. a = 3 - odcięta punktu styku.
2. f(3) = – 2.
3. fa "(x) \u003d x 2 - 4, fa "(3) \u003d 5.
y \u003d - 2 + 5 (x - 3), y \u003d 5x - 17 to równanie styczne.

Zadanie 2. Napisz równania wszystkich stycznych do wykresu funkcji y = - x 2 - 4x + 2, przechodzącej przez punkt M(- 3; 6).

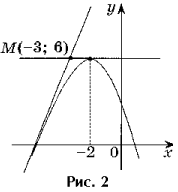Rozwiązanie. Punkt M(– 3; 6) nie jest punktem stycznym, ponieważ f(– 3) 6 (ryc. 2).

2. f(a) = – za 2 – 4a + 2.
3. f "(x) \u003d - 2x - 4, f "(a) \u003d - 2a - 4.
4. y \u003d - a 2 - 4a + 2 - 2 (a + 2) (x - a) - równanie styczne.

Styczna przechodzi przez punkt M(– 3; 6), więc jej współrzędne spełniają równanie stycznej.

6 = – za 2 – 4a + 2 – 2(a + 2)(– 3 – a),
za 2 + 6a + 8 = 0^ za 1 = - 4, za 2 = - 2.

Jeśli a = – 4, to równanie tangensa to y = 4x + 18.

Jeśli a \u003d - 2, to równanie styczne ma postać y \u003d 6.

W drugim typie kluczowymi zadaniami będą:

• styczna jest równoległa do pewnej prostej (zadanie 3);
• styczna przechodzi pod pewnym kątem do danej prostej (Zadanie 4).

Zadanie 3. Zapisz równania wszystkich stycznych do wykresu funkcji y \u003d x 3 - 3x 2 + 3, równolegle do linii y \u003d 9x + 1.

Rozwiązanie.

1. a - odcięta punktu styku.
2. f(a) = za 3 - 3a 2 + 3.
3. f "(x) \u003d 3x 2 - 6x, f "(a) \u003d 3a 2 - 6a.

Ale z drugiej strony f "(a) \u003d 9 (warunek równoległości). Musimy więc rozwiązać równanie 3a 2 - 6a \u003d 9. Jego pierwiastki a \u003d - 1, a \u003d 3 (ryc. 3).

4. 1) za = – 1;
2) f(– 1) = – 1;
3) fa "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 to równanie styczne;

1) za = 3;
2) f(3) = 3;
3) fa "(3) = 9;
4) y = 3 + 9(x - 3);

y = 9x – 24 to równanie styczne.

Zadanie 4. Napisz równanie stycznej do wykresu funkcji y = 0,5x 2 - 3x + 1, przechodzącej pod kątem 45 ° do prostej y = 0 (ryc. 4).

Rozwiązanie. Z warunku f "(a) \u003d tg 45 ° znajdujemy a: a - 3 \u003d 1^a=4.

1. a = 4 - odcięta punktu styku.
2. f(4) = 8 - 12 + 1 = - 3.
3. fa "(4) \u003d 4 - 3 \u003d 1.
4. y \u003d - 3 + 1 (x - 4).

y \u003d x - 7 - równanie stycznej.

Łatwo pokazać, że rozwiązanie dowolnego innego problemu sprowadza się do rozwiązania jednego lub kilku kluczowych problemów. Jako przykład rozważ następujące dwa problemy.

1. Napisz równania stycznych do paraboli y = 2x 2 - 5x - 2, jeżeli styczne przecinają się pod kątem prostym i jedna z nich dotyka paraboli w punkcie z odciętą 3 (ryc. 5).

Rozwiązanie. Ponieważ podana jest odcięta punktu styku, pierwsza część rozwiązania sprowadza się do kluczowego problemu 1.

1. a \u003d 3 - odcięta punktu styku jednego z boków kąta prostego.
2. f(3) = 1.
3. fa "(x) \u003d 4x - 5, fa "(3) \u003d 7.
4. y \u003d 1 + 7 (x - 3), y \u003d 7x - 20 - równanie pierwszej stycznej.

niech jest kątem nachylenia pierwszej stycznej. Ponieważ styczne są prostopadłe, to jest kątem nachylenia drugiej stycznej. Z równania y = 7x – 20 pierwszej stycznej mamy tg a = 7. Znajdź

Oznacza to, że nachylenie drugiej stycznej wynosi .

Dalsze rozwiązanie sprowadza się do kluczowego zadania 3.

Niech zatem B(c; f(c)) będzie punktem stycznym drugiej prostej

1. - odcięta drugiego punktu kontaktu.
2.
3.
4.
jest równaniem drugiej stycznej.

Notatka. Współczynnik kątowy stycznej można znaleźć łatwiej, jeśli uczniowie znają stosunek współczynników prostych prostopadłych k 1 k 2 = - 1.

2. Zapisz równania wszystkich wspólnych stycznych do wykresów funkcji

Rozwiązanie. Zadanie sprowadza się do znalezienia odciętych punktów styku wspólnych stycznych, czyli rozwiązania kluczowego problemu 1 w postaci ogólnej, zestawienia układu równań, a następnie rozwiązania go (ryc. 6).

1. Niech a będzie odciętą punktu styku leżącego na wykresie funkcji y = x 2 + x + 1.
2. f(a) = za 2 + za + 1.
3. fa "(a) = 2a + 1.
4. y \u003d za 2 + za + 1 + (2a + 1) (x - a) \u003d (2a + 1) x + 1 - za 2.

1. Niech c będzie odciętą punktu stycznego leżącego na wykresie funkcji
2.
3. fa "(c) = do.
4.

Skoro styczne są wspólne, to

Więc y = x + 1 i y = - 3x - 3 są wspólnymi stycznymi.

Głównym celem rozważanych zadań jest przygotowanie studentów do samorozpoznania typu kluczowego zadania przy rozwiązywaniu bardziej złożonych zadań wymagających określonych umiejętności badawczych (umiejętność analizowania, porównywania, uogólniania, stawiania hipotez itp.). Takie zadania obejmują każde zadanie, w którym zadanie kluczowe jest zawarte jako składnik. Rozważmy jako przykład problem (odwrotny do problemu 1) znalezienia funkcji z rodziny jej stycznych.

3. Dla jakiego b i c są proste y \u003d x i y \u003d - 2x styczne do wykresu funkcji y \u003d x 2 + bx + c?

Rozwiązanie.

Niech t będzie odciętą punktu styku prostej y = x z parabolą y = x 2 + bx + c; p jest odciętą punktu styku prostej y = - 2x z parabolą y = x 2 + bx + c. Wówczas równanie styczne y = x przyjmie postać y = (2t + b)x + c - t 2 , a równanie styczne y = - 2x przyjmie postać y = (2p + b)x + c - p 2 .

Skomponuj i rozwiąż układ równań

Odpowiedź:

Zadania do samodzielnego rozwiązania

1. Zapisz równania stycznych narysowanych do wykresu funkcji y = 2x 2 - 4x + 3 w punktach przecięcia wykresu z linią y = x + 3.

Odpowiedź: y \u003d - 4x + 3, y \u003d 6x - 9,5.

2. Dla jakich wartości a styczna narysowana do wykresu funkcji y \u003d x 2 - ax w punkcie wykresu z odciętą x 0 \u003d 1 przechodzi przez punkt M (2; 3) ?

Odpowiedź: a = 0,5.

3. Dla jakich wartości p prosta y = px - 5 dotyka krzywej y = 3x 2 - 4x - 2?

Odpowiedź: p 1 \u003d - 10, p 2 \u003d 2.

4. Znajdźcie wszystkie wspólne punkty wykresu funkcji y = 3x - x 3 i styczną poprowadzoną do tego wykresu przez punkt P(0; 16).

Odpowiedź: A(2; - 2), B(- 4; 52).

5. Znajdź najkrótszą odległość między parabolą y = x 2 + 6x + 10 a prostą

Odpowiedź:

6. Na krzywej y \u003d x 2 - x + 1 znajdź punkt, w którym styczna do wykresu jest równoległa do linii y - 3x + 1 \u003d 0.

Odpowiedź: M(2; 3).

7. Napisz równanie stycznej do wykresu funkcji y = x 2 + 2x - | 4x | który dotyka go w dwóch punktach. Narysuj coś.

Odpowiedź: y = 2x - 4.

8. Wykaż, że prosta y = 2x – 1 nie przecina krzywej y = x 4 + 3x 2 + 2x. Znajdź odległość między ich najbliższymi punktami.

Odpowiedź:

9. Na paraboli y \u003d x 2 brane są dwa punkty z odciętymi x 1 \u003d 1, x 2 \u003d 3. Przez te punkty rysowana jest sieczna. W jakim punkcie paraboli styczna do niej będzie równoległa do siecznej? Napisz równania dla siecznej i tangensa.

Odpowiedź: y \u003d 4x - 3 - sieczne równanie; y = 4x – 4 to równanie styczne.

10. Znajdź kąt q między stycznymi do wykresu funkcji y \u003d x 3 - 4x 2 + 3x + 1, narysowane w punktach z odciętymi 0 i 1.

Odpowiedź: q = 45°.

11. W jakich punktach styczna do wykresu funkcji tworzy z osią Ox kąt 135°?

Odpowiedź: A(0; - 1), B(4; 3).

12. W punkcie A(1; 8) do krzywej rysowana jest styczna. Znajdź długość odcinka stycznego zawartego między osiami współrzędnych.

Odpowiedź:

13. Napisz równanie wszystkich wspólnych stycznych do wykresów funkcji y \u003d x 2 - x + 1 i y \u003d 2x 2 - x + 0,5.

Odpowiedź: y = - 3x i y = x.

14. Znajdź odległość między stycznymi do wykresu funkcji równolegle do osi x.

Odpowiedź:

15. Określ, pod jakim kątem parabola y \u003d x 2 + 2x - 8 przecina oś x.

Odpowiedź: q 1 \u003d arctan 6, q 2 \u003d arctan (- 6).

16. Na wykresie funkcji znajdź wszystkie punkty, w których styczna do tego wykresu przecina dodatnie półosie współrzędnych, odcinając od nich równe segmenty.

Odpowiedź: A(-3; 11).

17. Prosta y = 2x + 7 i parabola y = x 2 – 1 przecinają się w punktach M i N. Znajdź punkt przecięcia K prostych stycznych do paraboli w punktach M i N.

Odpowiedź: K(1; - 9).

18. Dla jakich wartości b linia y \u003d 9x + b jest styczna do wykresu funkcji y \u003d x 3 - 3x + 15?

Odpowiedź 1; 31.

19. Dla jakich wartości k prosta y = kx – 10 ma tylko jeden punkt wspólny z wykresem funkcji y = 2x 2 + 3x – 2? Dla znalezionych wartości k określ współrzędne punktu.

Odpowiedź: k 1 = - 5, A(- 2; 0); k 2 = 11, B(2; 12).

20. Dla jakich wartości b styczna poprowadzona do wykresu funkcji y = bx 3 – 2x 2 – 4 w punkcie z odciętymi x 0 = 2 przechodzi przez punkt M(1; 8)?

Odpowiedź: b = - 3.

21. Parabola z wierzchołkiem na osi x jest styczna do prostej przechodzącej przez punkty A(1; 2) i B(2; 4) w punkcie B. Znajdź równanie paraboli.

Odpowiedź:

22. Przy jakiej wartości współczynnika k parabola y \u003d x 2 + kx + 1 dotyka osi Ox?

Odpowiedź: k = q 2.

23. Znajdź kąty między prostą y = x + 2 a krzywą y = 2x 2 + 4x - 3.

29. Znajdź odległość między stycznymi do wykresu generatorów funkcji z dodatnim kierunkiem osi Ox pod kątem 45 °.

Odpowiedź:

30. Znajdź miejsce wierzchołków wszystkich parabol postaci y = x 2 + ax + b stykających się z prostą y = 4x - 1.

Odpowiedź: prosta y = 4x + 3.

Literatura

1. Zvavich LI, Shlyapochnik L.Ya., Chinkina M.V. Algebra i początki analizy: 3600 problemów dla uczniów i kandydatów na uniwersytety . - M., Drop, 1999.
2. Mordkovich A. Czwarte seminarium dla młodych nauczycieli. Temat to „Aplikacje pochodne”. - M., "Matematyka", nr 21/94.
3. Kształtowanie wiedzy i umiejętności w oparciu o teorię stopniowego przyswajania działań umysłowych. / wyd. P.Ya. Galperin, NF Talyzina. - M., Moskiewski Uniwersytet Państwowy, 1968.

Styczna jest linią prostą , który dotyka wykresu funkcji w jednym punkcie i którego wszystkie punkty znajdują się w najmniejszej odległości od wykresu funkcji. Dlatego styczna przechodzi stycznie do wykresu funkcji pod pewnym kątem, a kilka stycznych nie może przechodzić przez punkt styczny pod różnymi kątami. Równania styczne i równania normalnej do wykresu funkcji są zestawiane za pomocą pochodnej.

Równanie styczne pochodzi z równania linii prostej .

Wyprowadzamy równanie stycznej, a następnie równanie normalnej do wykresu funkcji.

y = kx + B .

W nim k- współczynnik kątowy.

Stąd otrzymujemy następujący wpis:

y - y 0 = k(X - X 0 ) .

Wartość pochodna F "(X 0 ) Funkcje y = F(X) w punkcie X0 równe nachyleniu k=tg φ styczna do wykresu funkcji poprowadzonej przez punkt M0 (X 0 , y 0 ) , Gdzie y0 = F(X 0 ) . Co to jest geometryczne znaczenie pochodnej .

W ten sposób możemy wymienić k NA F "(X 0 ) i uzyskać następujące równanie stycznej do wykresu funkcji :

y - y 0 = F "(X 0 )(X - X 0 ) .

W zadaniach zestawiania równania stycznej do wykresu funkcji (do których wkrótce przejdziemy) wymagane jest doprowadzenie równania otrzymanego z powyższego wzoru do ogólne równanie linii prostej. Aby to zrobić, musisz przenieść wszystkie litery i cyfry na lewą stronę równania i pozostawić zero po prawej stronie.

Teraz o równaniu normalnym. Normalna jest linią prostą przechodzącą przez punkt styczny do wykresu funkcji prostopadłej do stycznej. Normalne równanie :

(X - X 0 ) + F "(X 0 )(y - y 0 ) = 0

Aby rozgrzać pierwszy przykład, zostaniesz poproszony o samodzielne rozwiązanie go, a następnie przyjrzyj się rozwiązaniu. Istnieją wszelkie powody, aby mieć nadzieję, że zadanie to nie będzie „zimnym prysznicem” dla naszych czytelników.

Przykład 0. Skomponuj równanie stycznej i równanie normalnej do wykresu funkcji w punkcie M (1, 1) .

Przykład 1 Ułóż równanie stycznej i równanie normalnej do wykresu funkcji jeśli odcięta punktu styku to .

Znajdźmy pochodną funkcji:

Teraz mamy wszystko, co trzeba podstawić do wpisu podanego w odnośniku teoretycznym, aby otrzymać równanie styczne. dostajemy

W tym przykładzie mieliśmy szczęście: nachylenie okazało się równe zeru, więc nie było potrzeby osobnego doprowadzania równania do ogólnej postaci. Teraz możemy napisać równanie normalne:

Na poniższym obrazku: wykres funkcji w kolorze bordowym, styczna na zielono, normalna na pomarańczowo.

Następny przykład również nie jest skomplikowany: funkcja, podobnie jak w poprzednim, również jest wielomianem, ale współczynnik nachylenia nie będzie równy zeru, więc zostanie dodany jeszcze jeden krok - doprowadzenie równania do postaci ogólnej.

Przykład 2

Rozwiązanie. Znajdźmy rzędną punktu styku:

Znajdźmy pochodną funkcji:

.

Znajdźmy wartość pochodnej w punkcie styku, czyli nachylenie stycznej:

Podstawiamy wszystkie otrzymane dane do „pustej formuły” i otrzymujemy równanie styczne:

Doprowadzamy równanie do ogólnej postaci (zbieramy wszystkie litery i cyfry inne niż zero po lewej stronie i zostawiamy zero po prawej stronie):

Tworzymy równanie normalnej:

Przykład 3 Skomponuj równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta punktu styku wynosi .

Rozwiązanie. Znajdźmy rzędną punktu styku:

Znajdźmy pochodną funkcji:

.

Znajdźmy wartość pochodnej w punkcie styku, czyli nachylenie stycznej:

.

Znajdujemy równanie stycznej:

Zanim doprowadzisz równanie do ogólnej postaci, musisz je trochę „połączyć”: pomnożyć termin po terminie przez 4. Robimy to i doprowadzamy równanie do ogólnej postaci:

Tworzymy równanie normalnej:

Przykład 4 Skomponuj równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta punktu styku wynosi .

Rozwiązanie. Znajdźmy rzędną punktu styku:

.

Znajdźmy pochodną funkcji:

Znajdźmy wartość pochodnej w punkcie styku, czyli nachylenie stycznej:

.

Otrzymujemy równanie styczne:

Doprowadzamy równanie do postaci ogólnej:

Tworzymy równanie normalnej:

Częstym błędem podczas pisania równań stycznych i normalnych jest niezauważenie, że funkcja podana w przykładzie jest zespolona i obliczenie jej pochodnej jako pochodnej funkcji prostej. Poniższe przykłady już są złożone funkcje(odpowiednia lekcja otworzy się w nowym oknie).

Przykład 5 Skomponuj równanie stycznej i równanie normalnej do wykresu funkcji, jeśli odcięta punktu styku wynosi .

Rozwiązanie. Znajdźmy rzędną punktu styku:

Uwaga! Ta funkcja jest złożona, ponieważ argument tangensa (2 X) sama jest funkcją. Dlatego znajdujemy pochodną funkcji jako pochodną funkcji zespolonej.

Instrukcja

Określamy nachylenie stycznej do krzywej w punkcie M.
Krzywa przedstawiająca wykres funkcji y = f(x) jest ciągła w pewnym sąsiedztwie punktu M (włączając sam punkt M).

Jeśli wartość f’(x0) nie istnieje, to albo nie ma stycznej, albo przechodzi ona pionowo. W związku z tym obecność pochodnej funkcji w punkcie x0 wynika z istnienia niepionowej stycznej, która styka się z wykresem funkcji w punkcie (x0, f(x0)). W tym przypadku nachylenie stycznej będzie równe f "(x0). Zatem geometryczne znaczenie pochodnej staje się jasne - obliczenie nachylenia stycznej.

Znajdź wartość odciętej punktu styku, który jest oznaczony literą „a”. Jeśli pokrywa się z danym punktem stycznym, to „a” będzie jego współrzędną x. Określ wartość Funkcje f(a), podstawiając do równania Funkcje rozmiar odciętej.

Wyznacz pierwszą pochodną równania Funkcje f'(x) i podstawiamy do niego wartość punktu "a".

Weź ogólne równanie stycznej, które jest zdefiniowane jako y \u003d f (a) \u003d f (a) (x - a) i zastąp znalezione wartości a, f (a), f "( a) W rezultacie rozwiązanie wykresu zostanie znalezione i styczne.

Rozwiąż zadanie inaczej, jeśli podany punkt styczny nie pokrywa się z punktem stycznym. W takim przypadku konieczne jest podstawienie „a” zamiast liczb w równaniu stycznym. Następnie zamiast liter „x” i „y” zastąp wartość współrzędnych danego punktu. Rozwiąż otrzymane równanie, w którym „a” jest niewiadomą. Umieść wynikową wartość w równaniu tangensa.

Napisz równanie dla stycznej z literą „a”, jeśli równanie jest podane w warunku zadania Funkcje oraz równanie prostej równoległej względem pożądanej stycznej. Następnie potrzebujesz pochodnej Funkcje do współrzędnej w punkcie „a”. Podstaw odpowiednią wartość do równania tangensa i rozwiąż funkcję.