D(f)- ती मूल्ये जी युक्तिवाद घेऊ शकतात, उदा. कार्य व्याप्ती.

E(f)- ती मूल्ये जी फंक्शन घेऊ शकतात, उदा. कार्य मूल्यांचा संच.

फंक्शन्सच्या श्रेणी शोधण्याच्या पद्धती.

जटिल फंक्शन वितर्कांच्या मूल्यांचा अनुक्रमिक शोध;

स्कोअरिंग/बाऊंड्री पद्धत;

फंक्शनची सातत्य आणि मोनोटोनिसिटीच्या गुणधर्मांचा वापर;

डेरिव्हेटिव्हचा वापर;

फंक्शनची सर्वात मोठी आणि सर्वात लहान मूल्ये वापरणे;

ग्राफिक पद्धत;

पॅरामीटर परिचय पद्धत;

व्यस्त कार्य पद्धत.

चला त्यापैकी काहींचा विचार करूया.

व्युत्पन्न वापरणे

सामान्य दृष्टीकोनसतत फंक्शन f(x) च्या व्हॅल्यूजचा संच शोधणे म्हणजे फंक्शन f(x) ची सर्वात मोठी आणि सर्वात लहान व्हॅल्यू त्याच्या डोमेनमध्ये शोधणे (किंवा हे सिद्ध करणे की एक किंवा दोन्ही अस्तित्वात नाहीत) .

आपल्याला फंक्शनच्या मूल्यांचा संच शोधण्याची आवश्यकता असल्यास विभागावर:

दिलेल्या फंक्शनचे व्युत्पन्न शोधा f "(x);

फंक्शन f(x) चे गंभीर बिंदू शोधा आणि दिलेल्या विभागाशी संबंधित ते निवडा;

विभागाच्या शेवटी आणि निवडलेल्या गंभीर बिंदूंवर फंक्शनच्या मूल्यांची गणना करा;

सापडलेल्या मूल्यांपैकी, सर्वात लहान आणि सर्वात मोठी मूल्ये निवडा;

फंक्शन व्हॅल्यूजचा संच या व्हॅल्यूजमध्ये काढला जातो.

फंक्शनची व्याप्ती असल्यास मध्यांतर, नंतर तीच योजना वापरली जाते, परंतु टोकावरील मूल्यांऐवजी, जेव्हा युक्तिवाद मध्यांतराच्या टोकाकडे झुकतो तेव्हा फंक्शनच्या मर्यादा वापरल्या जातात. मधील मर्यादा मूल्ये मूल्य सेटमध्ये समाविष्ट केलेली नाहीत.

सीमा/स्कोअर पद्धत

फंक्शन व्हॅल्यूचा संच शोधण्यासाठी, प्रथम वितर्क मूल्यांचा संच शोधा आणि नंतर फंक्शन फंक्शनची संबंधित किमान आणि कमाल मूल्ये शोधा. असमानता वापरून - सीमा निश्चित करा.

सार म्हणजे खाली आणि वरून सतत फंक्शनचा अंदाज लावणे आणि हे सिद्ध करणे की फंक्शन अंदाजांच्या खालच्या आणि वरच्या सीमेपर्यंत पोहोचते. या प्रकरणात, अंदाजाच्या खालच्या सीमारेषेपासून वरच्या एकापर्यंतच्या मध्यांतरासह फंक्शनच्या मूल्यांच्या संचाचा योगायोग फंक्शनच्या सातत्य आणि त्यासाठी इतर मूल्यांच्या अनुपस्थितीद्वारे निर्धारित केला जातो.

सतत फंक्शनचे गुणधर्म

दुसरा पर्याय म्हणजे फंक्शनला सतत मोनोटोनिक फंक्शनमध्ये रूपांतरित करणे, नंतर असमानतेचे गुणधर्म वापरून, नवीन प्राप्त केलेल्या फंक्शनच्या मूल्यांच्या संचाचा अंदाज लावला जातो.

जटिल फंक्शन आर्ग्युमेंट्सची अनुक्रमिक मूल्ये शोधणे

फंक्शन बनवणाऱ्या इंटरमीडिएट फंक्शन्सच्या व्हॅल्यूजच्या सेटसाठी अनुक्रमिक शोधावर आधारित

मूलभूत प्राथमिक कार्यांच्या श्रेणी

कार्य	अनेक मूल्ये
$y = kx+ b$	E(y) = (-∞;+∞)
$y = x^(2n)$	E(y) =
$y = \cos(x)$	E(y) = [-1;1]
$y = (\rmtg)\, x$	E(y) = (-∞;+∞)
$y = (\rm ctg)\, x$	E(y) = (-∞;+∞)
$y = \arcsin(x)$	E(y) = [-π/2; π/2]
$y = \arccos(x)$	E(y) =
$y = (\rm arctg)\, x$	E(y) = (-π/2; π/2)
$y = (\rm arcctg)\, x$	E(y) = (0; π)

उदाहरणे

फंक्शन व्हॅल्यूजचा संच शोधा:

व्युत्पन्न वापरणे

परिभाषाचे डोमेन शोधा: D(f)=[-3;3], कारण $9-x^(2)\geq 0$

व्युत्पन्न शोधा: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$

f"(x) = 0 जर x = 0. f"(x) अस्तित्वात नसेल तर $\sqrt(9-x^(2))=0$ म्हणजे x = ±3 साठी. आम्हाला तीन गंभीर बिंदू मिळतात: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, त्यापैकी दोन विभागाच्या टोकाशी जुळतात. गणना करा: f(–3) = 0, f(0) = 3, f(3) = 0. अशा प्रकारे, f(x) चे सर्वात लहान मूल्य 0 आहे, सर्वात मोठे मूल्य 3 आहे.

उत्तर: E(f) = .

व्युत्पन्न वापरत नाही

फंक्शनची सर्वात मोठी आणि सर्वात लहान मूल्ये शोधा:

$ पासून
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , नंतर:

$f(x)\leq \frac(3)(4)$ सर्व x साठी;

$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ सर्व x साठी(कारण $|\cos (x)|\leq 1$);

$f(\frac(\pi)(3))= frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2) )=\frac(3)(4)$;

$f(\pi)= frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;

उत्तर: $\frac(3)(4)$ आणि $-\frac(3)(2)$

जर तुम्ही डेरिव्हेटिव्ह्जच्या मदतीने ही समस्या सोडवली तर तुम्हाला फंक्शन f (x) हे सेगमेंटवर नव्हे तर संपूर्ण वास्तविक रेषेवर परिभाषित केले आहे या वस्तुस्थितीशी संबंधित अडथळ्यांवर मात करणे आवश्यक आहे.

सीमा/अंदाज पद्धती वापरणे

हे साइनच्या व्याख्येवरून पुढे येते की $-1\leq\sin(x)\leq 1$. पुढे, आम्ही संख्यात्मक असमानतेचे गुणधर्म वापरतो.

$-4\leq - 4\sin(x)\leq 4$, (दुहेरी असमानतेच्या सर्व तीन भागांना -4 ने गुणा);

$1\leq 5 - 4\sin(x)\leq 9$ (दुहेरी असमानता 5 च्या तीन भागांमध्ये जोडले);

हे फंक्शन संपूर्ण व्याख्येच्या डोमेनवर सतत असल्याने, त्याच्या मूल्यांचा संच त्याच्या सर्वांत लहान आणि सर्वात मोठ्या मूल्याच्या संपूर्ण व्याख्येच्या डोमेनवर असतो, जर असेल तर.

या प्रकरणात, फंक्शनच्या मूल्यांचा संच $y = 5 - 4\sin(x)$ हा संच आहे.

असमानता $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ वरून आम्हाला $$\\ -6\leq y\ अंदाज प्राप्त होतो. leq 6$ $

x = p आणि x = 0 साठी, फंक्शन -6 आणि 6 मूल्ये घेते, म्हणजे. खालच्या आणि वरच्या सीमांवर पोहोचते. सतत फंक्शन्स cos(7x) आणि cos(x) चे रेखीय संयोजन म्हणून, फंक्शन y पूर्ण संख्या अक्षावर सतत असते, म्हणून, सतत फंक्शनच्या गुणधर्मानुसार, ते -6 ते 6 पर्यंत सर्व मूल्ये घेते. , आणि फक्त तेच, कारण असमानतेमुळे $- 6\leq y\leq 6$ इतर मूल्ये अशक्य आहेत.

म्हणून, E(y) = [-6;6].

$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ उत्तर: E(f) = .

$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].

$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .

$$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left चे रूपांतर करू. ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left (\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.

कोसाइनची व्याख्या म्हणजे $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$

हे फंक्शन संपूर्ण व्याख्येच्या डोमेनवर सतत असल्याने, त्याच्या मूल्यांचा संच त्याच्या सर्वात लहान आणि सर्वात मोठ्या मूल्यामध्ये बंद केला जातो, जर असेल तर, $y =\sqrt(2)\ या फंक्शनच्या मूल्यांचा संच. cos(x +\frac(\pi)(4 )))$ हा $[-\sqrt(2);\sqrt(2)]$ आहे.

$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x) )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$

$t = 5 – (3^(x)+1)^(2)$, कुठे -∞≤t≤4 दर्शवा. अशा प्रकारे, किरण (-∞;4) वर $y = \log_(0,5)(t)$ फंक्शनच्या मूल्यांचा संच शोधण्यात समस्या कमी होते. फंक्शन $y = \log_(0,5)(t)$ फक्त t > 0 साठी परिभाषित केले असल्याने, किरण (-∞;4) वरील मूल्यांचा संच त्याच्या मूल्यांच्या संचाशी एकरूप होतो. इंटरव्हलवरील फंक्शन (0;4) हे दर्शविते किरण (-∞;4) चे छेदनबिंदू लॉगरिदमिक फंक्शनच्या (0;+∞) परिभाषेच्या डोमेनसह आहे. मध्यांतरावर (0;4) हे कार्य सतत आणि कमी होत आहे. t > 0 साठी, ते +∞ कडे झुकते आणि t = 4 साठी ते -2 मूल्य घेते, म्हणून E(y) = (-2, +∞).

आम्ही फंक्शनच्या ग्राफिक प्रतिनिधित्वावर आधारित तंत्र वापरतो.

फंक्शनच्या परिवर्तनानंतर, आमच्याकडे आहे: y 2 + x 2 = 25, आणि y ≥ 0, |x| ≤ ५.

हे लक्षात ठेवले पाहिजे की $x^(2)+y^(2)=r^(2)$ हे r त्रिज्या वर्तुळाचे समीकरण आहे.

या निर्बंधांतर्गत, या समीकरणाचा आलेख हा उगमस्थानी मध्यवर्ती असलेला वरचा अर्धवर्तुळ आहे आणि त्रिज्या 5 आहे. हे स्पष्ट आहे की E(y) = .

उत्तर: E(y) = .

संदर्भ

युनिफाइड स्टेट एक्झामिनेशन, मिनयुक इरिना बोरिसोव्हनाच्या कार्यांमधील कार्यांची व्याप्ती

फंक्शन व्हॅल्यूजचा संच शोधण्यासाठी टिपा, Belyaeva I., Fedorova S.

फंक्शन व्हॅल्यूजचा संच शोधत आहे

प्रवेश परीक्षेत गणितातील प्रश्न कसे सोडवायचे, I.I. मेलनिकोव्ह, I.N. Sergeev

GBOU lyceum (आर्थिक) सह. इसकला

गणिताचे शिक्षक कुझाएवा व्ही.एन.

2016

संदर्भ साहित्य

उपाय नमुनाफंक्शन व्हॅल्यूजचा संच शोधा

फंक्शन स्कोप
आहे

y - कोणतीही संख्या

फंक्शन स्कोप
आहे y - कोणतीही संख्या

अनेक मूल्ये

y - कोणतीही संख्या

सर्वोच्च मूल्य

सर्वात कमी मूल्य

डोमेन एक्स - कोणतीही संख्या
, कुठे

, कुठे

अनेक मूल्ये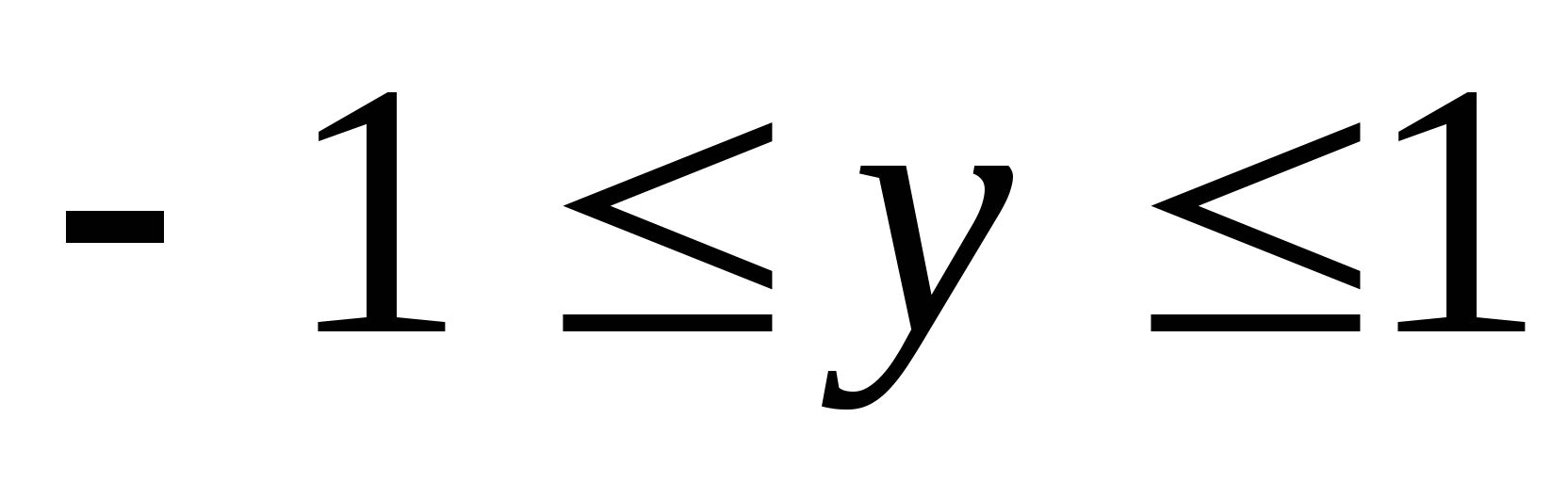
y - कोणतीही संख्याy - कोणतीही संख्या

काही त्रिकोणमितीय कार्यांसाठी प्लॉट टेम्पलेट्स

त्रिकोणमितीय कार्यांच्या मूल्यांचा संच

पर्याय 1

Y =पाप 3x+2.

1) (-5;5) 2) 3) 4) (1;5)

2. फंक्शन y = चे क्षेत्रफळ शोधाtg x + 1.

1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2

4. फंक्शनच्या श्रेणीतील सर्वात लहान पूर्णांक निर्दिष्ट करा

y = १२.७ + ५ पाप(3x-2).

1) -5 2) 8 3) 5 4) 17

5. फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच विभाग आहे [-2;2].

1) y = कारण 2x 2) y = पाप 2 x 3) y = कारण 2 x +2

4) y = 2 पाप 4 x

6. फंक्शन व्हॅल्यूजचा संच शोधाy = tg 2 xविभागावर

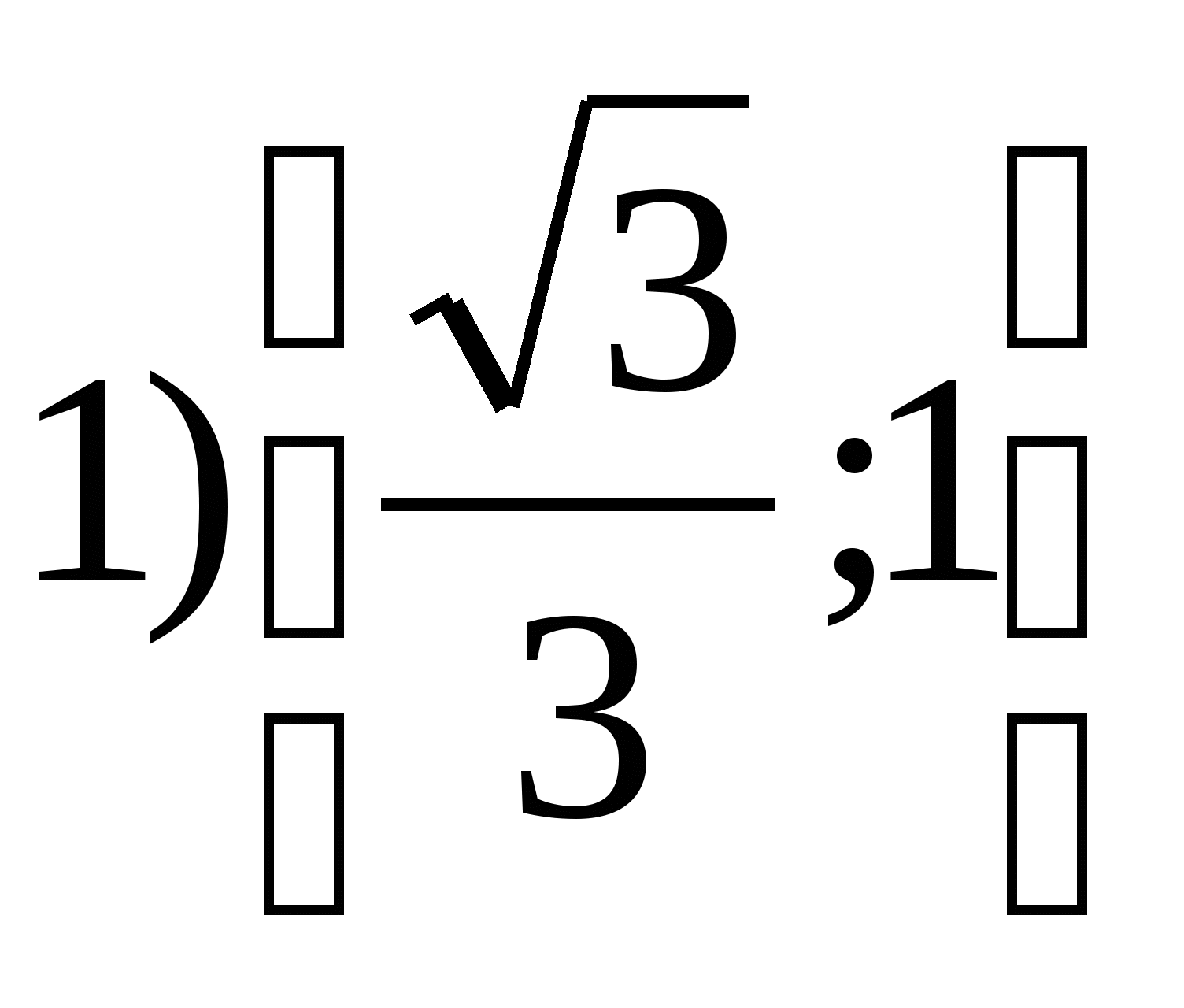
7. फंक्शनच्या श्रेणीतील सर्व पूर्णांकांची बेरीज शोधाy = 4 कारण 2 x – 7.

1) -25 2) 25 3) -22 4) 0

पर्याय २

y = 2 कारण 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. फंक्शनची व्याप्ती शोधा

1) 3) (-∞;∞) 4) .

3. फंक्शनच्या श्रेणीतील सर्वात लहान संख्या निर्दिष्ट करा

1) 4 2) -3 3) 1 4) -7

4. फंक्शनच्या श्रेणीतील सर्वात मोठा पूर्णांक निर्दिष्ट करा

1) 2 2) 13 3) 12 4) -2

5. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच विभाग आहे [-5;5].

1) y = पाप 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. फंक्शन व्हॅल्यूजचा संच शोधा
विभागावर

7. फंक्शन y \u003d 5 - 3 च्या श्रेणीतील सर्व पूर्णांकांचा गुणाकार शोधापाप 2 x.

1) 120 2) 14 3) -15 4) 0

पर्याय 3
1. फंक्शन व्हॅल्यूजचा संच निर्दिष्ट कराy = पाप 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. फंक्शन y = 5 च्या श्रेणीतील सर्वात लहान संख्या निर्दिष्ट कराtg 2 x+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच एक विभाग आहे

[-17;-13].

1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15

2) y = 2 cos x - 15 4) y = 3 sin x +10

6. फंक्शन व्हॅल्यूच्या सेटमध्ये समाविष्ट नसलेली सर्वात लहान नैसर्गिक संख्या दर्शवा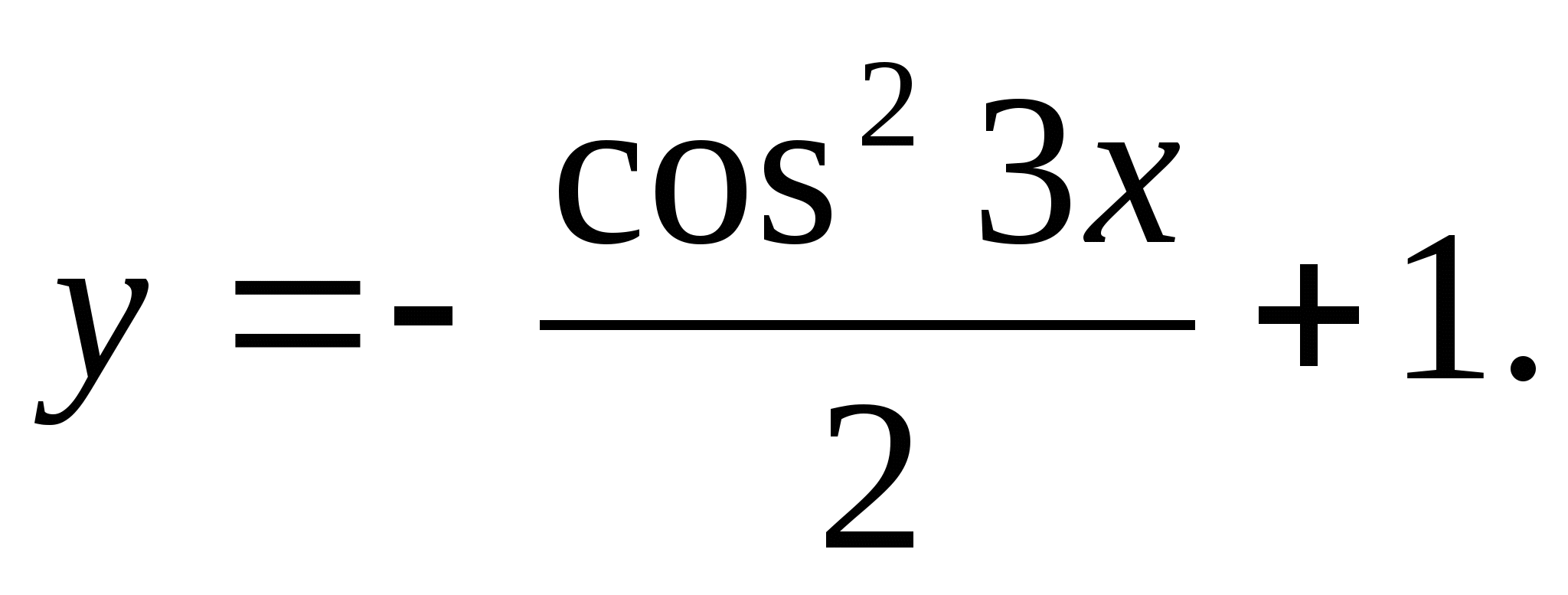

1) 2 2) 4 3) 15 4) 6

7. फंक्शन व्हॅल्यूजच्या सेटमध्ये किती पूर्णांक आहेत

y = 2 कारण 3 x +10?

1) 2 2) 3 3) 4 5) 5

पर्याय 4

1) 2) 4) (-7;-6)

2. फंक्शनची श्रेणी शोधा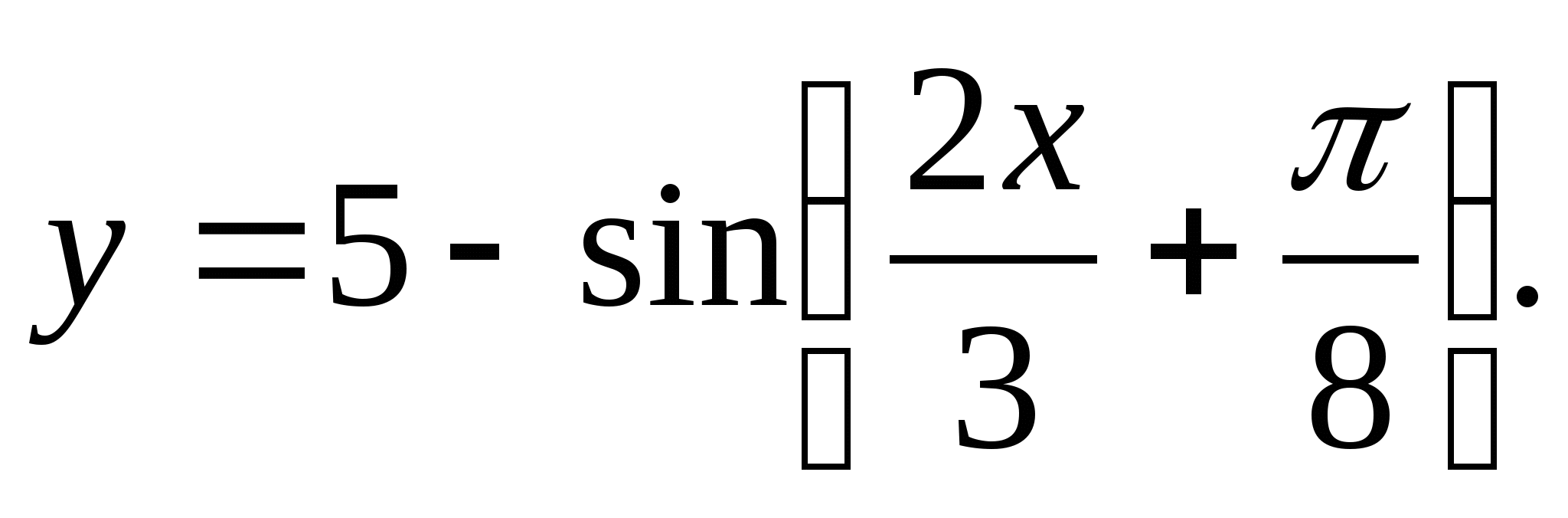

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. फंक्शनच्या श्रेणीतील सर्वात मोठी संख्या निर्दिष्ट कराy = -3 ctg 2 x+7.

1) 10 2) 4 3) 7 4) -3

4. खालीलपैकी कोणती संख्या फंक्शन व्हॅल्यूच्या सेटमध्ये समाविष्ट नाही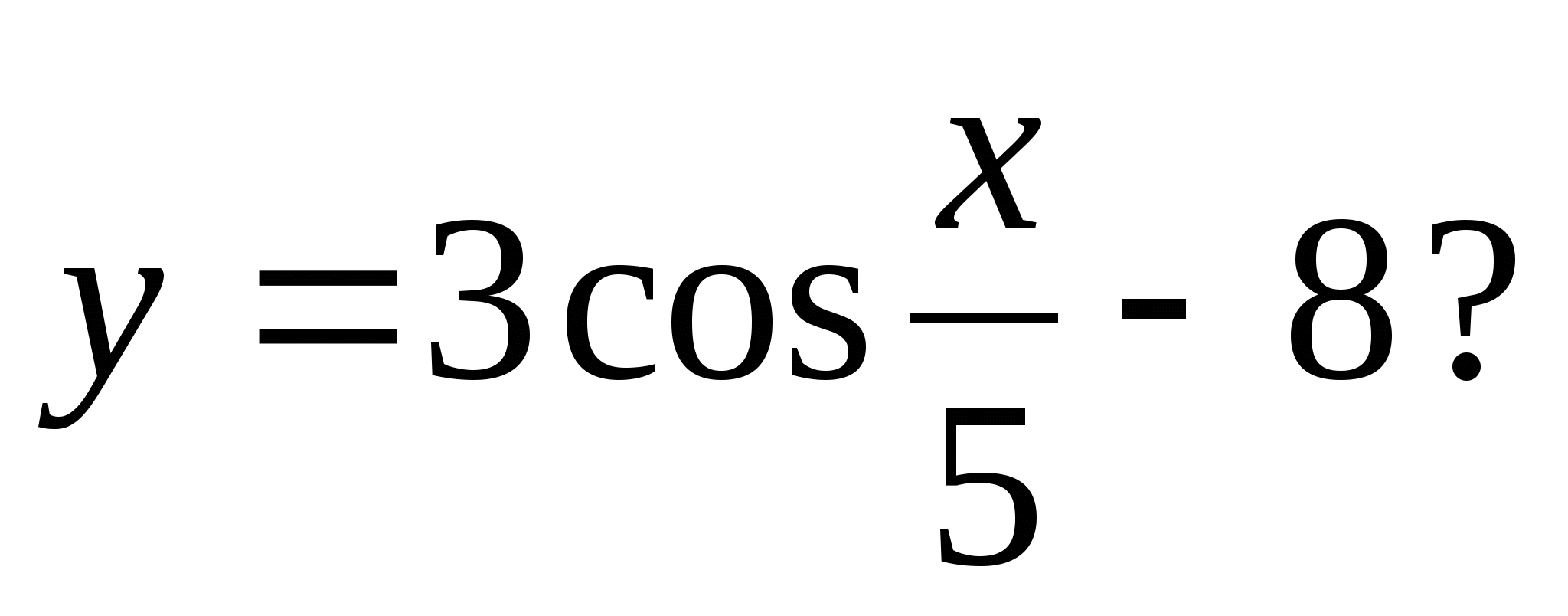

1) -6 2) -5 3) -10 4) -7

5. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच मध्यांतर आहे.

6. फंक्शनच्या श्रेणीमध्ये समाविष्ट नसलेला सर्वात मोठा ऋण पूर्णांक निर्दिष्ट करा

1) -1 2) -25 3) -6 4) -2

7. फंक्शन व्हॅल्यूजच्या सेटमध्ये किती पूर्णांक आहेत

1) 11 2) 3 3) 5 4) 4

पर्याय 5

1. फंक्शन व्हॅल्यूजचा सेट निर्दिष्ट करा y = 2 -पाप 5 x.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. फंक्शनची श्रेणी शोधा

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. फंक्शनच्या श्रेणीतील सर्वात लहान पूर्णांक निर्दिष्ट करा

y = 3 + पाप 2 2 x.

1) 0 2) 1 3) 3 4) 4

4. खालीलपैकी कोणती संख्या फंक्शन व्हॅल्यूच्या सेटमध्ये समाविष्ट आहे

1) 128 2) 10,5 3) 3 4) -235

5. फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच विभाग आहे [-9;15].

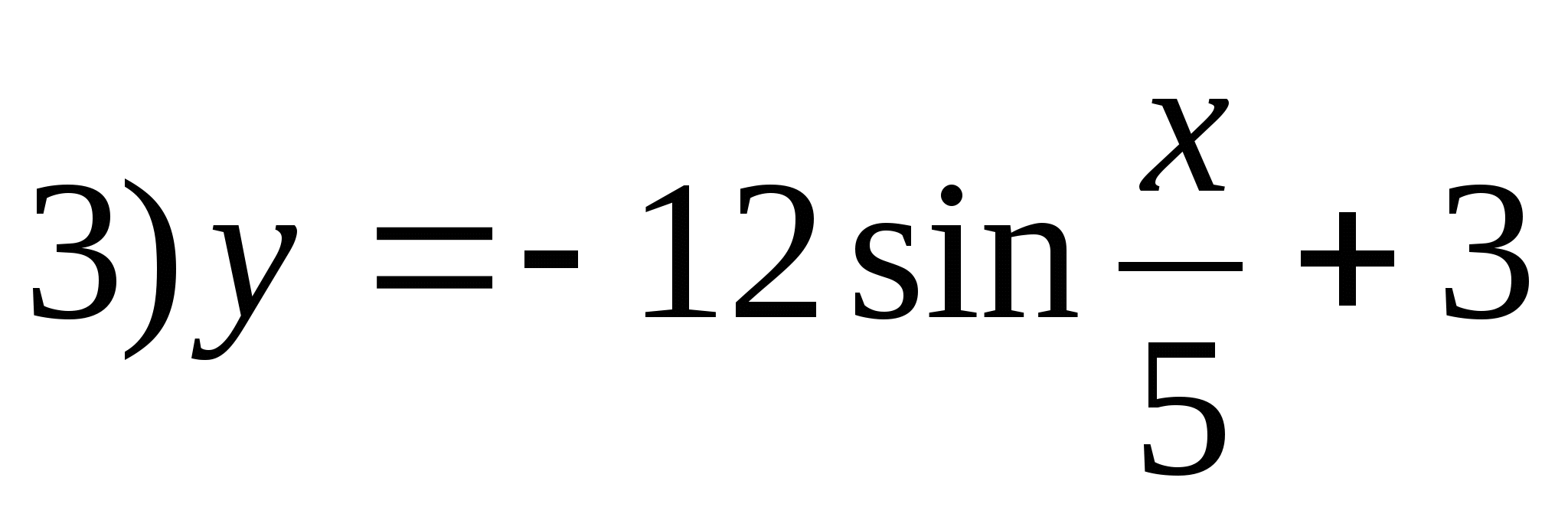
6. फंक्शन व्हॅल्यूच्या सेटमध्ये समाविष्ट केलेल्या पूर्णांकांची बेरीज शोधा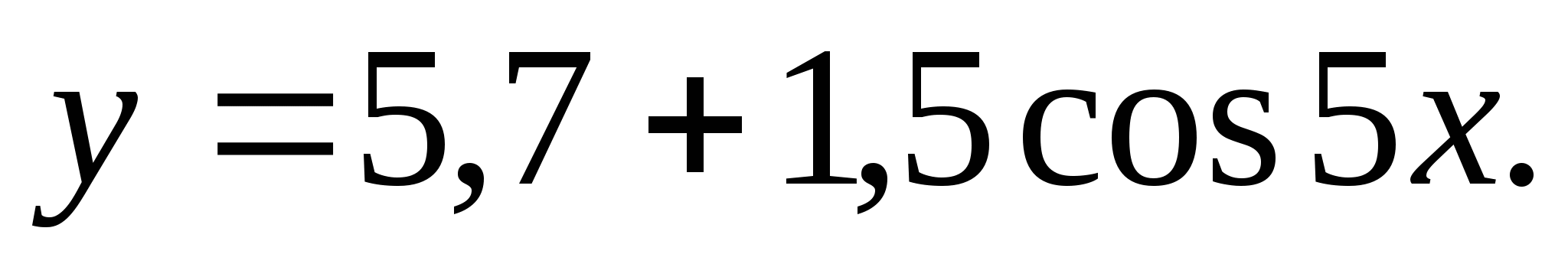

1) 0 2) 7 3) 18 4) 22

7. फंक्शनचे सर्वात मोठे मूल्य शोधा
विभागावर

1) 0,5 2) 1,5 3) 0 4) 2

पर्याय 6

1. फंक्शन व्हॅल्यूच्या संचाशी संबंधित विभाग निर्दिष्ट करा

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. फंक्शनची श्रेणी शोधा

3. फंक्शनच्या श्रेणीतील सर्वात मोठी संख्या निर्दिष्ट करा

1) 5 2) -6 3) -3 4) 4

4. खालीलपैकी कोणती संख्या फंक्शन व्हॅल्यूच्या सेटमध्ये समाविष्ट आहे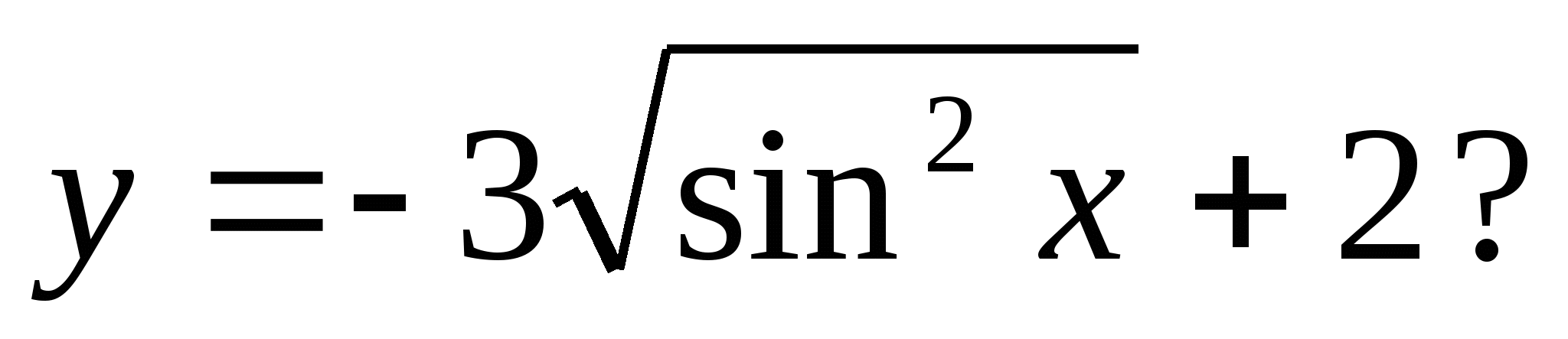

1) 5 2) 0 3) -3 4) 4

5. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच मध्यांतर आहे.

1) येथे = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 कारण 4 x 4) y = - tg 2 x + 1

6. मूल्यांच्या संचामध्ये समाविष्ट असलेल्या पूर्णांकांचे गुणाकार शोधा

y = 3,8 – 1,4 पाप 3 x.

1) 17 2) 12 3) 0 4) 60

7. फंक्शन व्हॅल्यूजचा संच शोधा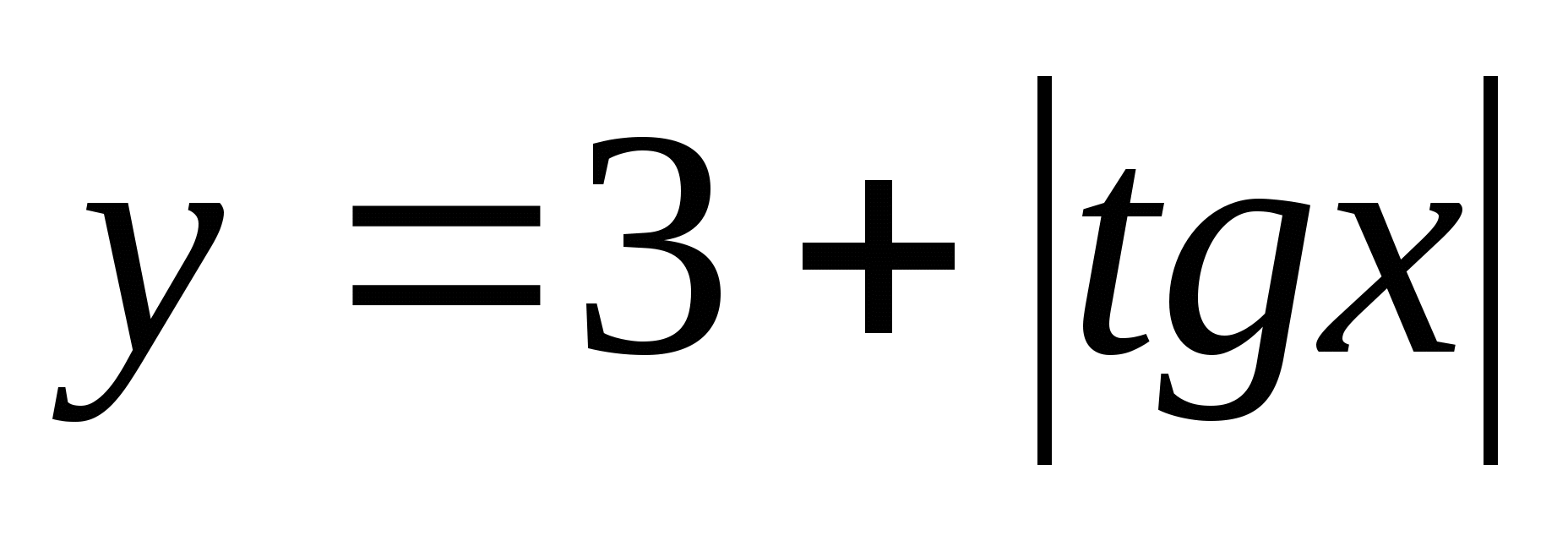
दरम्यान

1) (3;4) 2) 3)

पर्याय 7

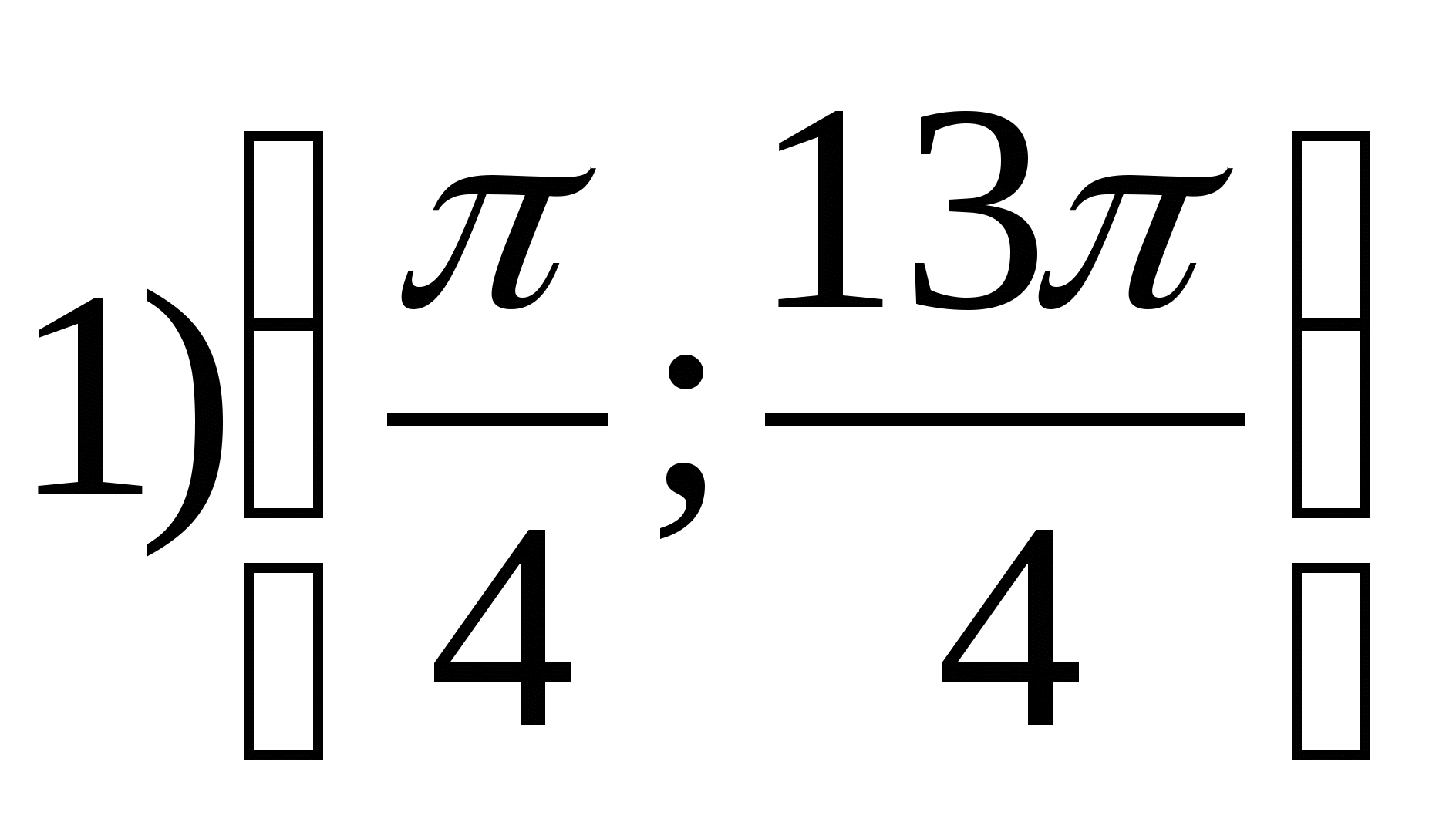
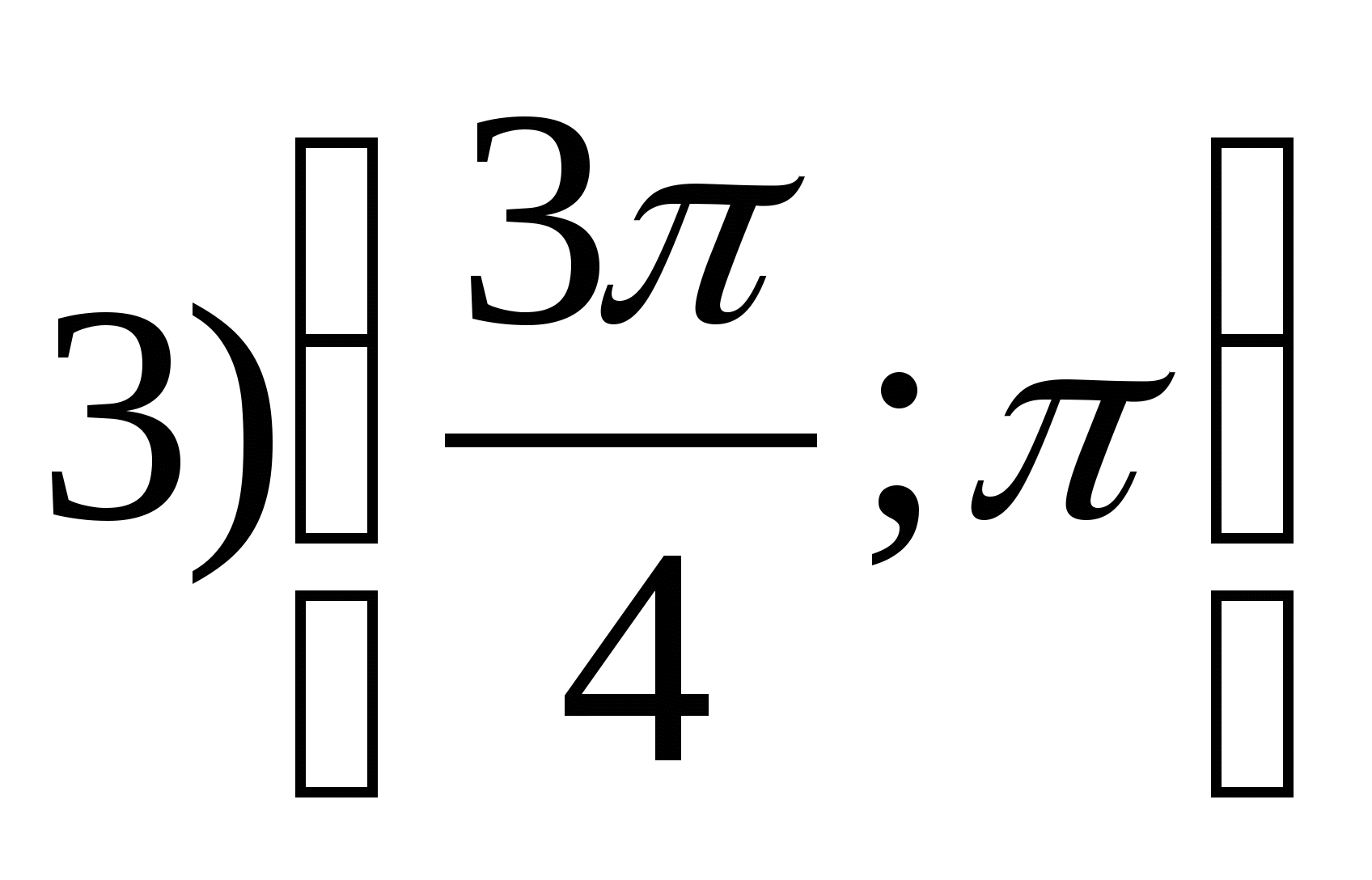
2. फंक्शनचे सर्वात लहान पूर्णांक मूल्य शोधा

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. समीकरण कोणत्या मूल्यांसाठी करतेपाप(3 x-4)+5= aसोडवण्यायोग्य?

1) 2) 3) (4;6) 4) (-6;4]

पाप 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

दरम्यान

2) 0 3) 1

y = 4 पाप(x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

पर्याय 8

1. फंक्शन व्हॅल्यूजचा संच शोधाy = arctgx- 2π.

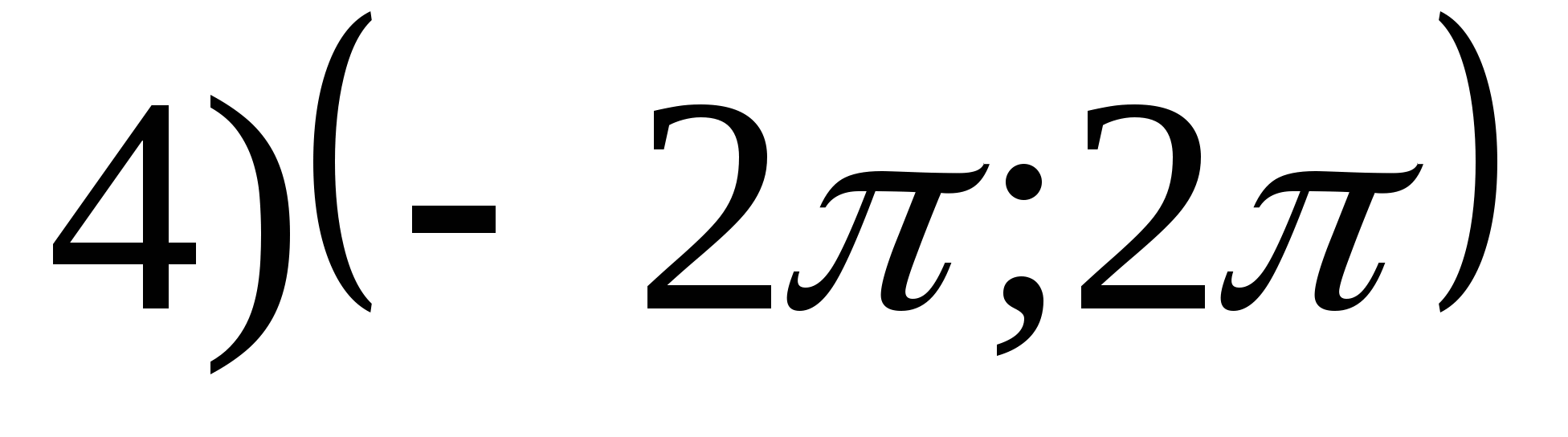
2. फंक्शनचे सर्वात मोठे मूल्य शोधा

1) 1,75 2) 0 3) 2,25 4) -1,75

3. खालीलपैकी कोणती संख्या फंक्शनची व्हॅल्यू असू शकते

1) -4 2) -2 3) 0 4) 2

4. p समीकरण -2+ च्या मूल्यांसाठीकारण(4 x-1)= pमुळे आहेत?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. फंक्शन व्हॅल्यूजचा संच शोधाy = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

दरम्यान
.

1) 0 2) 1 3) -1 4) 3

7. फंक्शनच्या रेंजमध्ये किती पूर्णांक आहेत

1) 4 2) 3 3) 5 4) 2

पर्याय 9

1. फंक्शनची श्रेणी शोधा

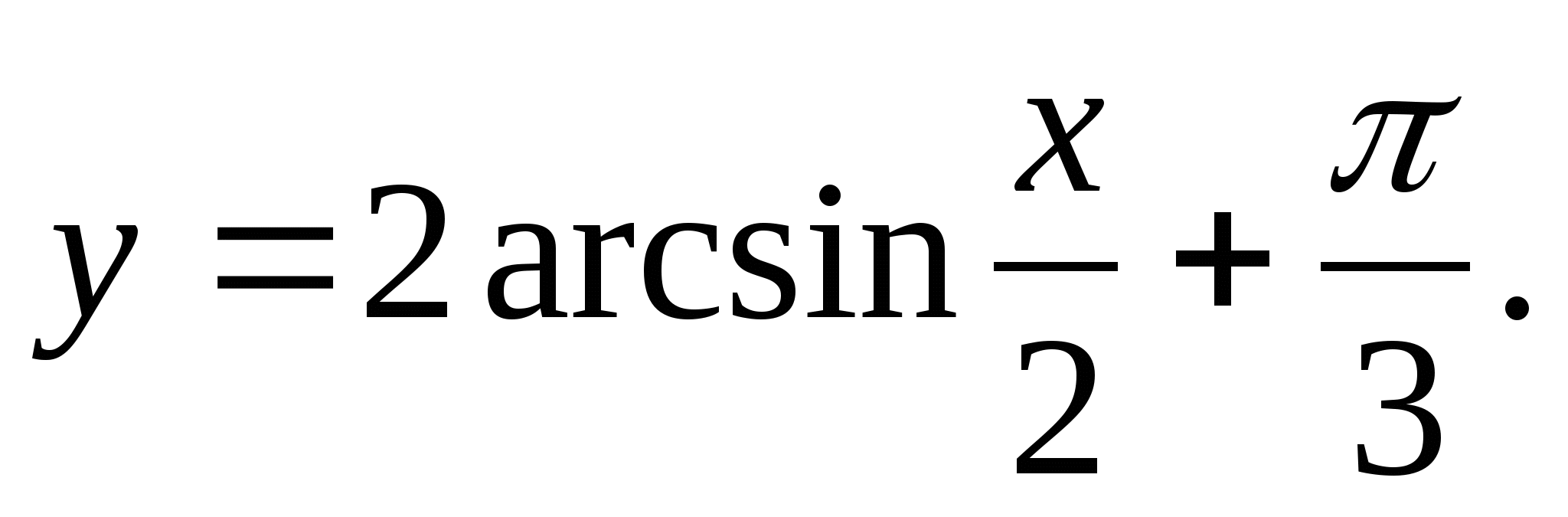
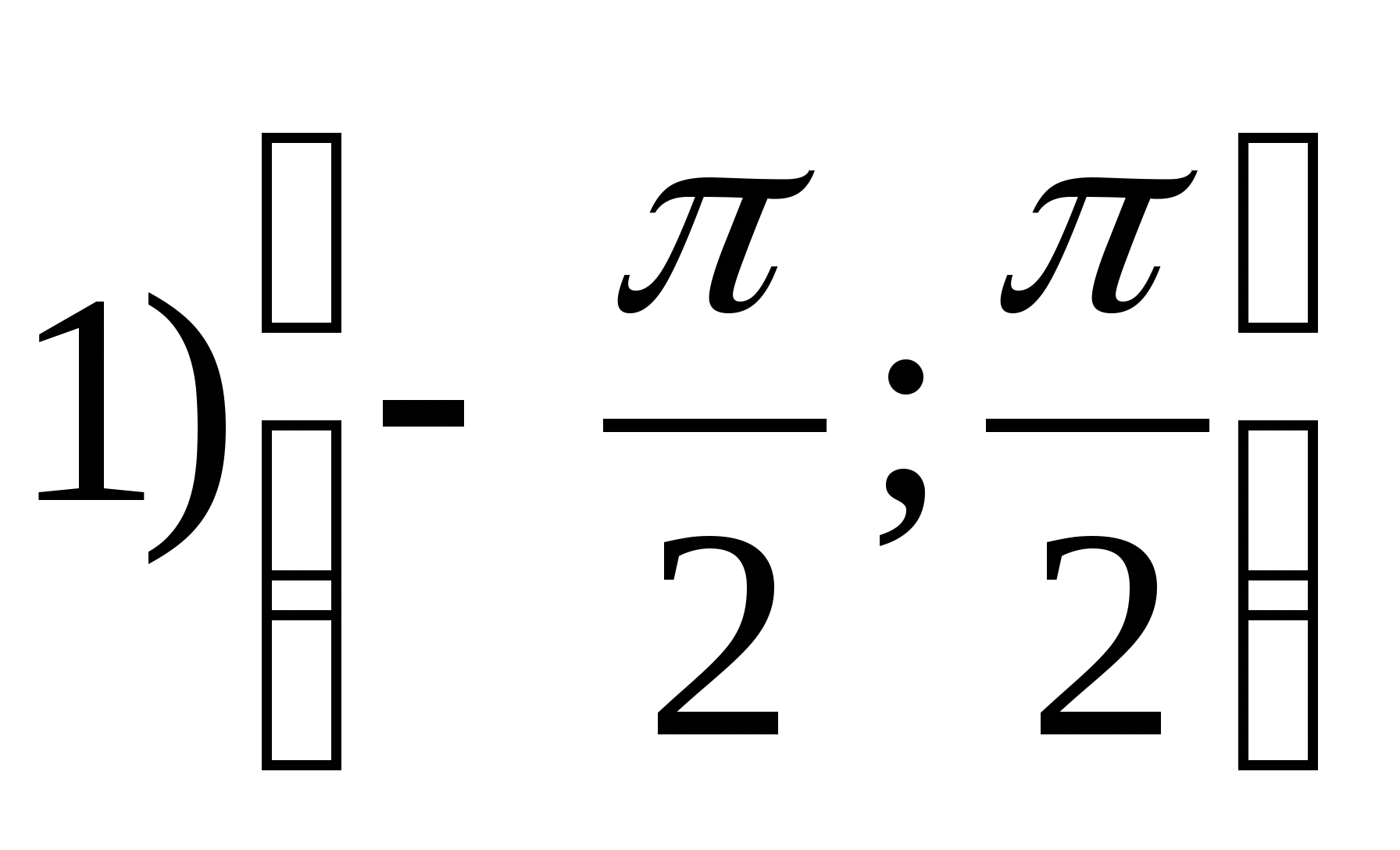
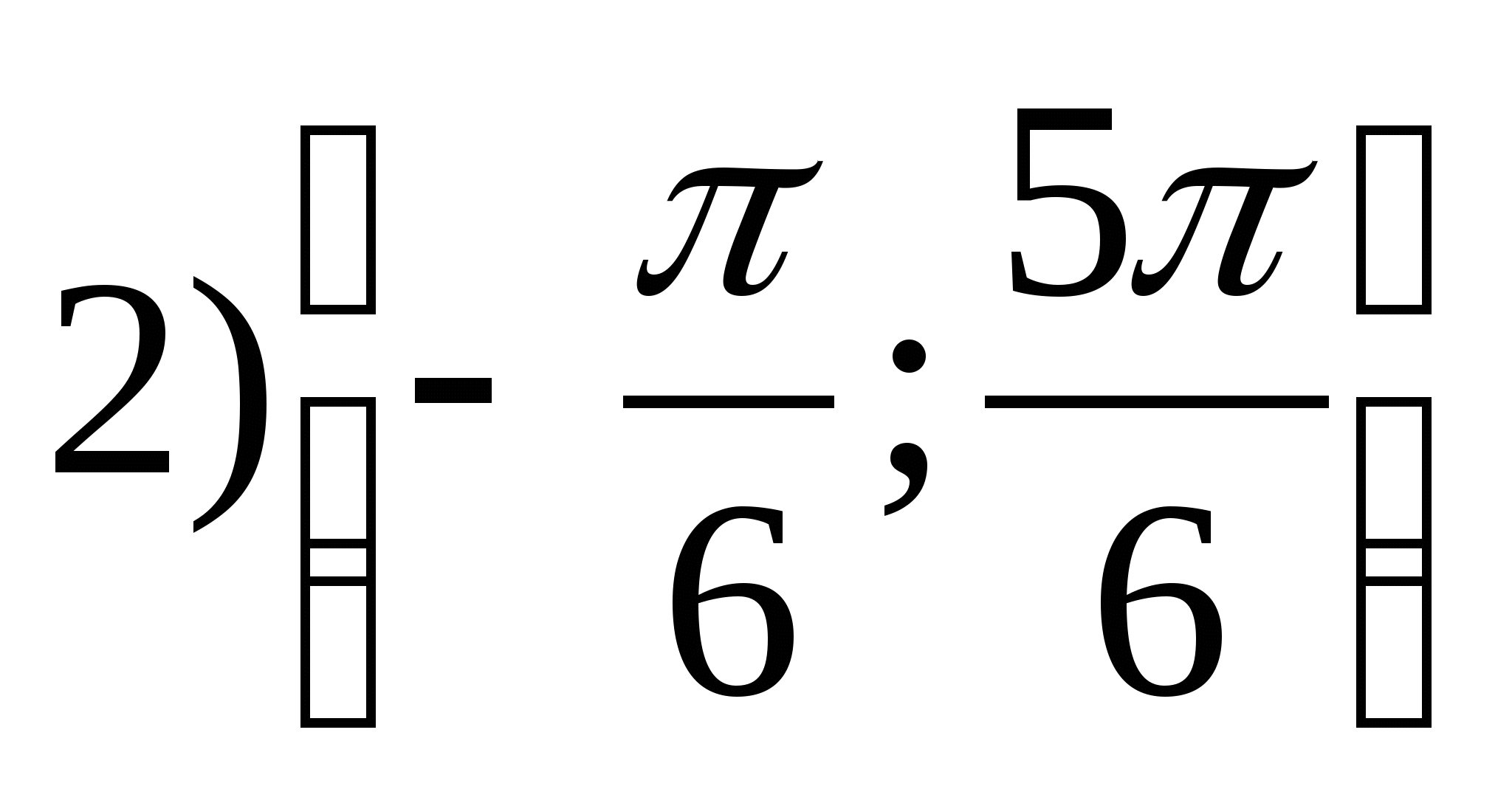
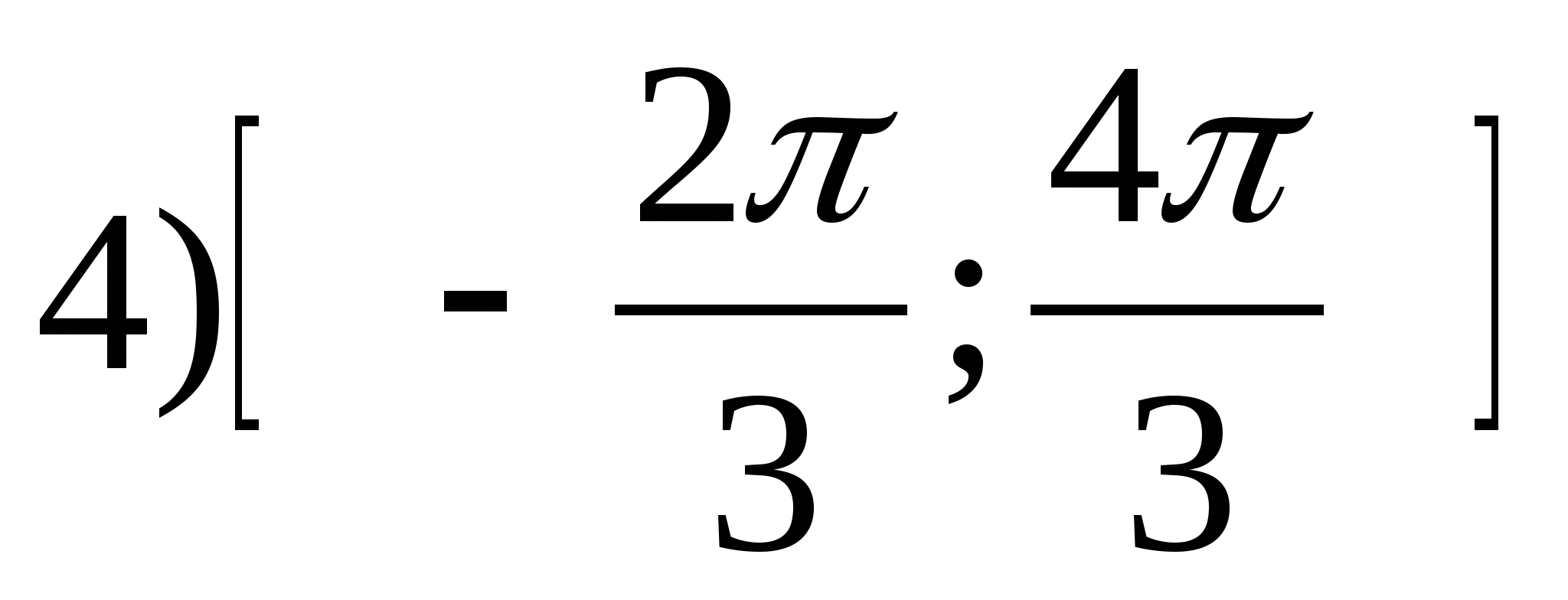
2. फंक्शनचे सर्वात मोठे पूर्णांक मूल्य शोधा

1) 4 2) 5 3) 6 4) 7

3. खालीलपैकी कोणती संख्या फंक्शनची व्हॅल्यू असू शकते

1) 0 2) 3 3) 6 4) 9

kसमीकरण - k + पाप(2 x-1) = 2 सोडवण्यायोग्य?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. फंक्शन व्हॅल्यूजचा संच शोधा \u200b\u200 द्वारे \u003d -कारण 2 3 x + 4.

1) 2) 3) 4)

6. फंक्शनचे सर्वात लहान मूल्य निर्दिष्ट करा
दरम्यान

2) -1 3) 0 4) 1

7. फंक्शन y = 12 च्या श्रेणीमध्ये किती पूर्णांक आहेत ते शोधाकारण 3 x +5 पाप 3 x.

1) 13 2) 27 3) 26 4) 14

पर्याय 10

1. फंक्शनची श्रेणी शोधा

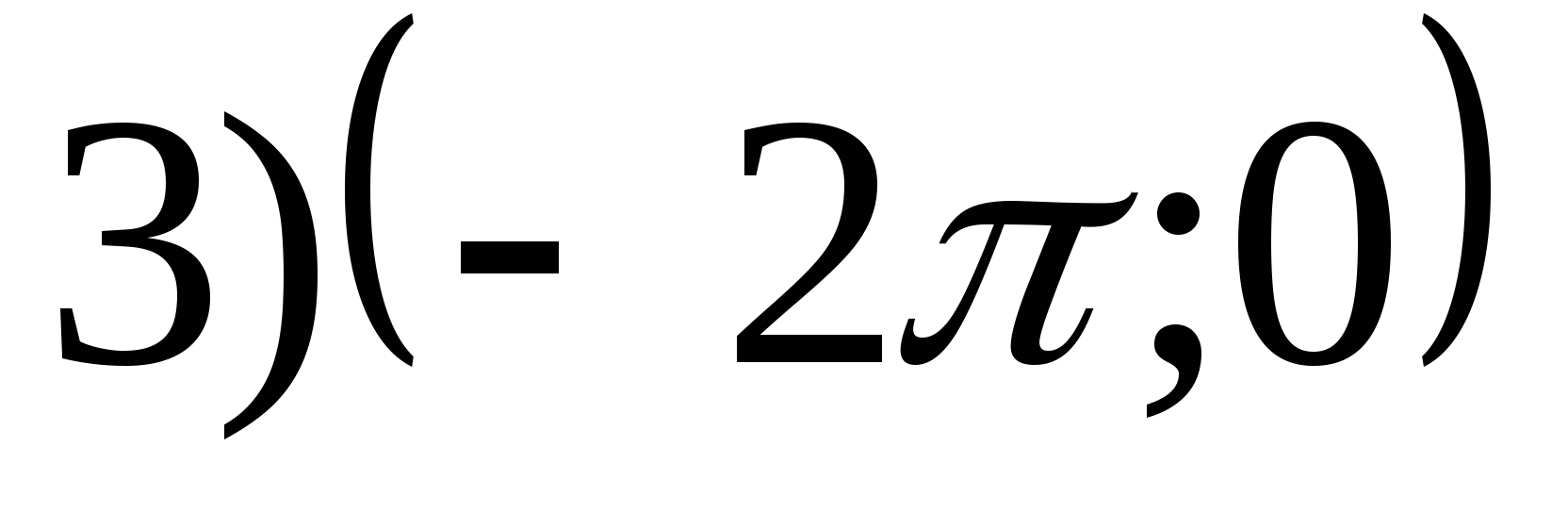
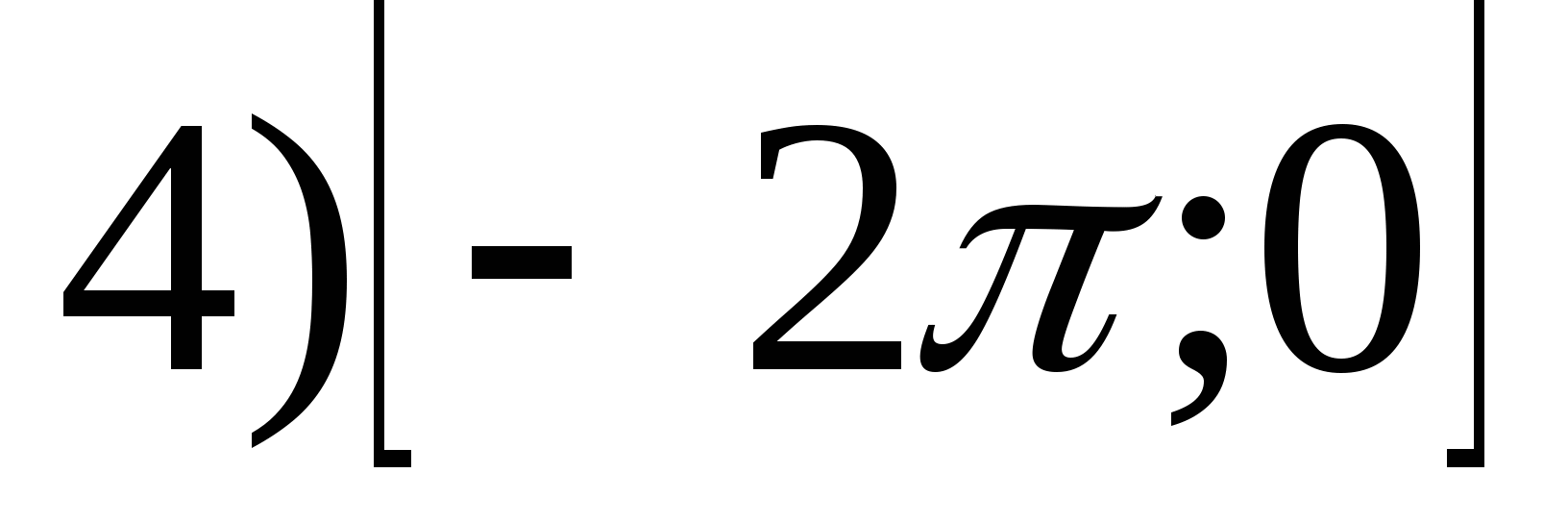
2. फंक्शनचे सर्वात लहान मूल्य शोधा

1) 3,5 2) 0 3) 2,5 4) -3,5

3. खालीलपैकी कोणती संख्या फंक्शनची व्हॅल्यू असू शकते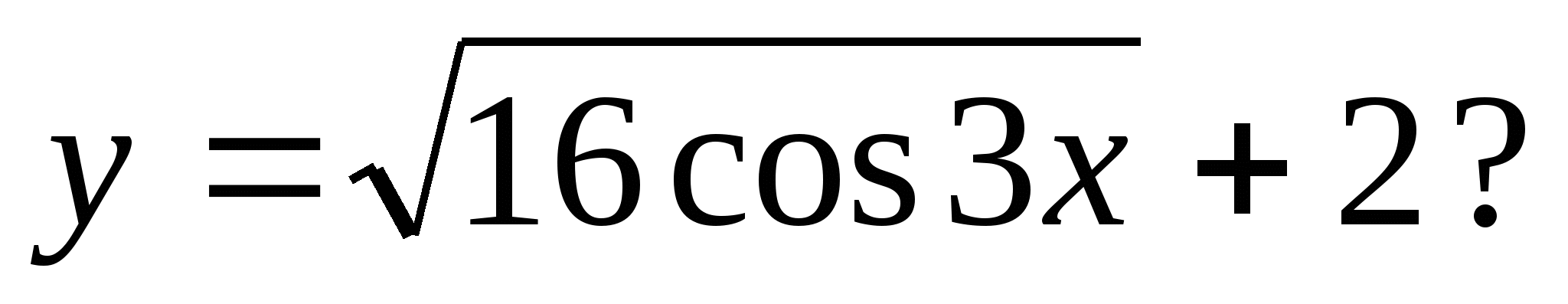

1) -4 2) -1 3) 3 4) 7

4. पॅरामीटरच्या कोणत्या मूल्यांवरमीसमीकरण कारण (3 x + 2)- मी= 5 ची मुळे आहेत?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. \u003d -2 द्वारे फंक्शन मूल्यांचा संच शोधाctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. फंक्शनचे सर्वात मोठे मूल्य निर्दिष्ट करा
दरम्यान

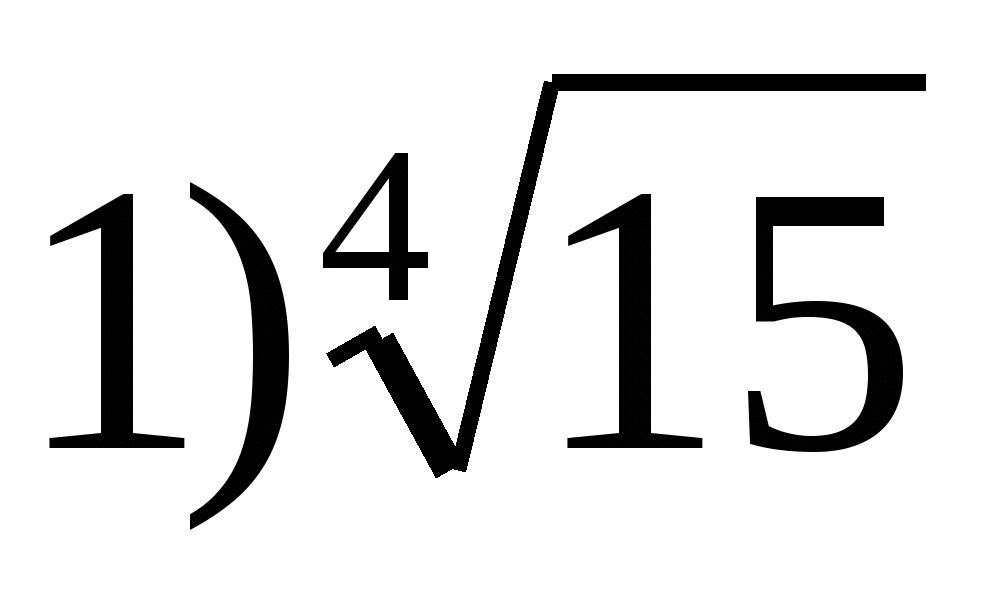2) 0 3) 2 4) 1

7. फंक्शनच्या रेंजमध्ये किती पूर्णांक आहेत ते शोधा

1) 30 2) 35 3) 17 4) 7

घातांकीय आणि लॉगरिदमिक फंक्शन्सच्या मूल्यांचा संच

पर्याय 1

1. फंक्शनची श्रेणी शोधा

1) 4) (-∞;3)

2. फंक्शन व्हॅल्यूजचा संच निर्दिष्ट करा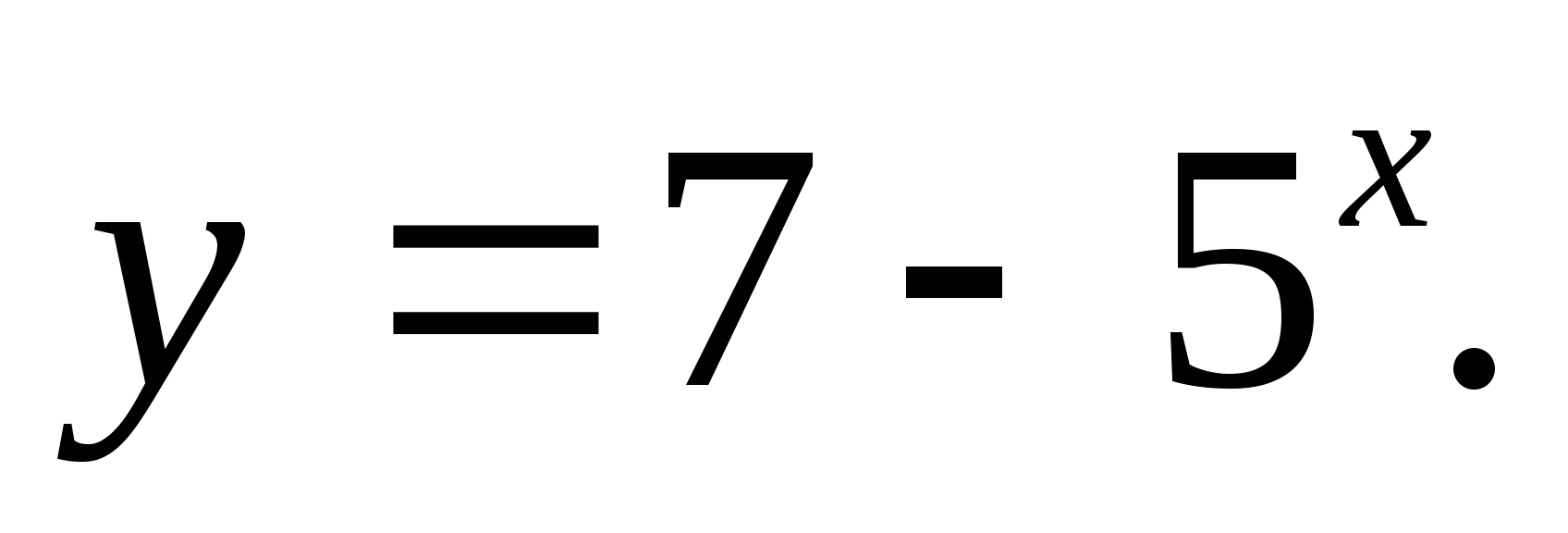

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. फंक्शनचे सर्वात लहान पूर्णांक मूल्य निर्दिष्ट करा

1) 1 2) -1 3) 0 4) -5

7. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच मध्यांतर (1;∞) आहे.

पर्याय २

1. फंक्शन व्हॅल्यूजचा संच निर्दिष्ट करा

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. फंक्शनची श्रेणी शोधा

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. फंक्शनचे सर्वात लहान पूर्णांक मूल्य निर्दिष्ट करा

1) -12 2) -11 3) -10 4) -15

4. फंक्शन व्हॅल्यूच्या संचाशी संबंधित नसलेली संख्या निर्दिष्ट करा

1) -42 2) 3 3) 1 4) -20

5. फंक्शन व्हॅल्यूजचा संच निर्दिष्ट करा

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. फंक्शनचे सर्वात मोठे पूर्णांक मूल्य निर्दिष्ट करा

1) 10 2) 3 3) 9 4) 2

7. एक फंक्शन निर्दिष्ट करा ज्याच्या मूल्यांचा संच मध्यांतर आहे

(-∞;13).

पर्याय 5

1. फंक्शनचे सर्वात लहान पूर्णांक मूल्य निर्दिष्ट करा

1) 0 2) -1 3) -2 4) -3

2. खालीलपैकी कोणती संख्या फंक्शनच्या रेंजमध्ये आहे

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. फंक्शन कोणत्या सेगमेंटवर आहे ते शोधा
2 चे सर्वात मोठे मूल्य आणि -3 चे सर्वात लहान मूल्य घेते.

1) 2) (-5;2) 3) 4) (-3;2)

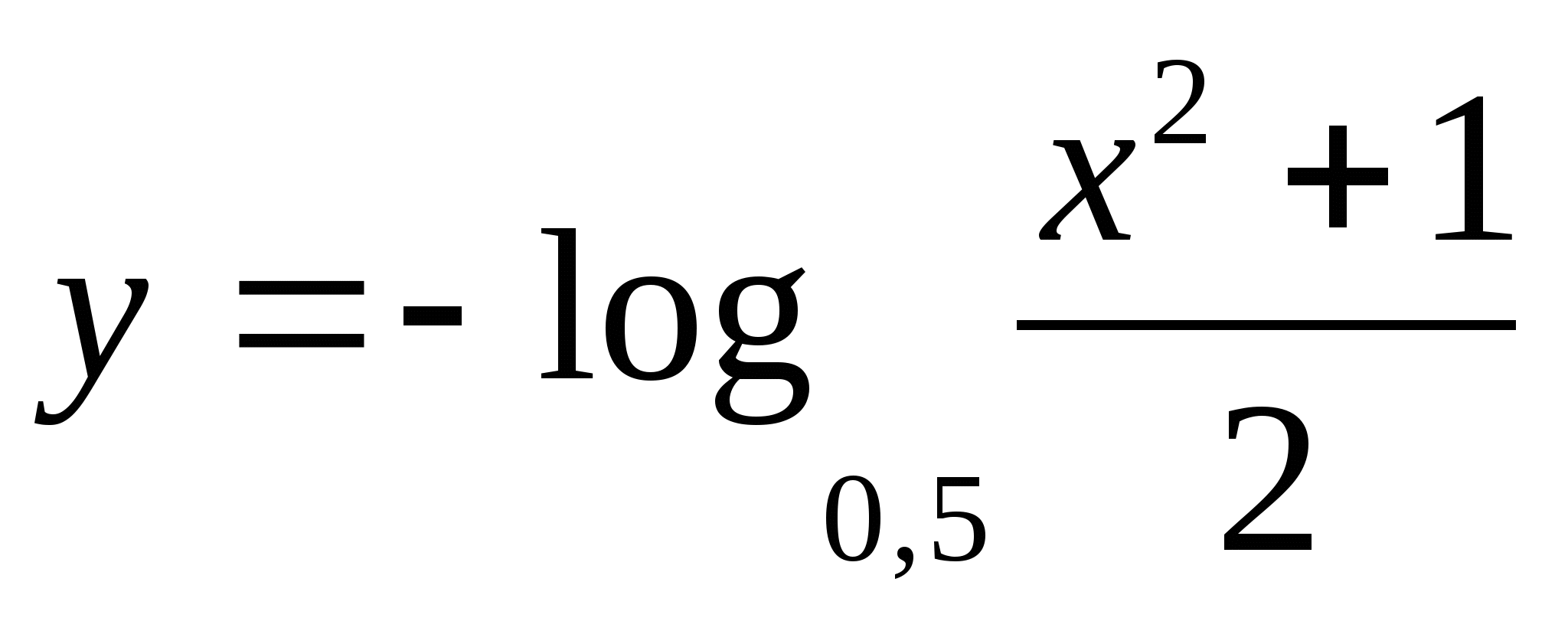दरम्यान

1) -1/2 2) 5 3) 2 4) 4

8. फंक्शनच्या मूल्य संचामध्ये समाविष्ट नसलेल्या सर्व नैसर्गिक संख्यांची बेरीज शोधा

1) 3 2) 6 3) 10 4) 8

पर्याय 6

1. फंक्शनचे सर्वात मोठे पूर्णांक मूल्य निर्दिष्ट करा

1) 2 2) 4 3) 3 4) 5

2. खालीलपैकी कोणती संख्या फंक्शनच्या रेंजमध्ये नाही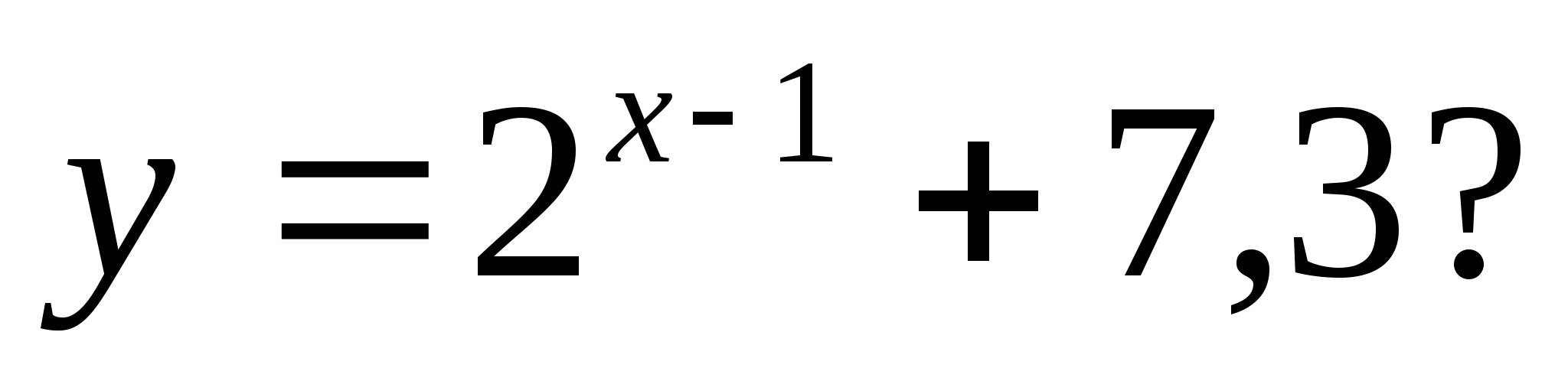

1) 35 2) 7, 28 3) 7, 85 4) 128

3. फंक्शन व्हॅल्यूजचा संच निर्दिष्ट करा

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. OU वरील सर्व बिंदू शोधा जे फंक्शनच्या आलेखाच्या बिंदूंचे अंदाज आहेत

1) (0;∞) 2) 2) (-3;2) 3) [ लॉग 2 3;2] 4) (लॉग 2 3;2)

6. फंक्शन कोणत्या सेगमेंटवर आहे ते शोधा
सर्वात लहान मूल्य -2 आणि सर्वात मोठे मूल्य 4 घेते.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. फंक्शनचे सर्वात मोठे मूल्य निर्दिष्ट करा
दरम्यान

[-0.9; 0]. 2. विभागावरील फंक्शनचे सर्वात लहान मूल्य शोधा.

4. फंक्शन किती पूर्णांक मूल्ये घेते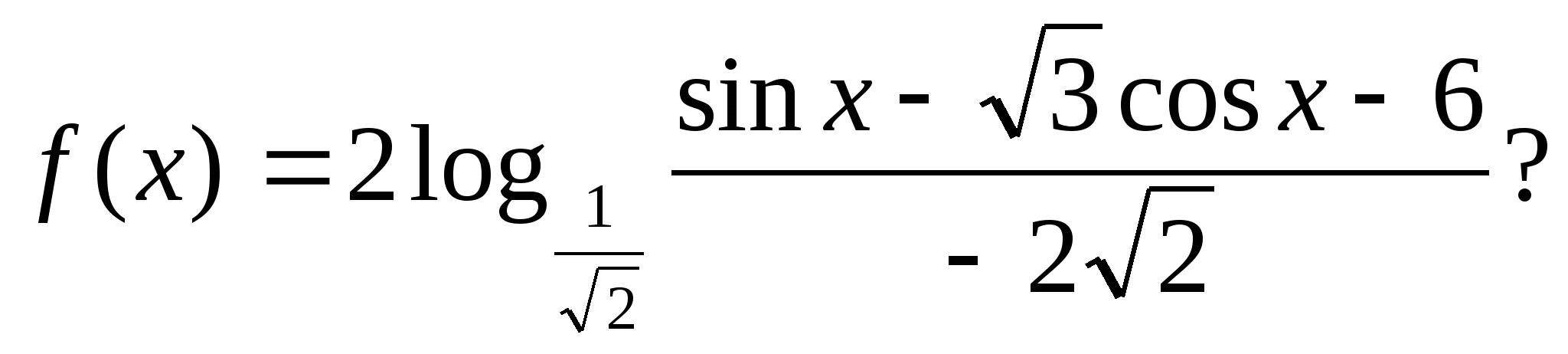

उत्तरे

भाग 1

घातांक आणि लॉगरिदमिक फंक्शन मूल्यांचा संच

भाग 2

फंक्शनची संकल्पना आणि त्याच्याशी जोडलेली प्रत्येक गोष्ट पारंपारिकपणे जटिल आहे, पूर्णपणे समजलेली नाही. फंक्शनचा अभ्यास आणि परीक्षेच्या तयारीमध्ये एक विशेष अडथळे म्हणजे परिभाषाचे क्षेत्र आणि कार्याच्या मूल्यांची श्रेणी (बदल).
बर्‍याचदा, विद्यार्थ्यांना फंक्शनचे डोमेन आणि त्याच्या व्हॅल्यूजच्या डोमेनमधील फरक दिसत नाही.
आणि जर विद्यार्थी फंक्शनच्या परिभाषाचे डोमेन शोधण्याच्या कार्यात प्रभुत्व मिळवतात, तर फंक्शनच्या मूल्यांचा संच शोधण्याच्या कार्यांमुळे त्यांना मोठ्या अडचणी येतात.
या लेखाचा उद्देशः फंक्शनची मूल्ये शोधण्याच्या पद्धतींशी परिचित होणे.
या विषयाच्या विचाराच्या परिणामी, सैद्धांतिक सामग्रीचा अभ्यास केला गेला, कार्य मूल्यांचे संच शोधण्याच्या समस्या सोडवण्याच्या पद्धतींचा विचार केला गेला, विद्यार्थ्यांच्या स्वतंत्र कार्यासाठी उपदेशात्मक सामग्री निवडली गेली.
या लेखाचा उपयोग शिक्षक विद्यार्थ्यांना अंतिम आणि प्रवेश परीक्षांची तयारी करण्यासाठी, गणिताच्या वैकल्पिक अभ्यासक्रमांमधील पर्यायी वर्गांमध्ये “कार्यक्षेत्राची व्याप्ती” या विषयाचा अभ्यास करताना करू शकतात.

I. फंक्शनची व्याप्ती निश्चित करणे.

y = f(x) फंक्शनच्या E(y) मूल्यांचे क्षेत्रफळ (संच) y 0 अशा संख्यांचा संच आहे, ज्यापैकी प्रत्येकासाठी x 0 अशी संख्या आहे की: f(x 0) = y 0 .

मुख्य प्राथमिक फंक्शन्सच्या रेंज आठवूया.

एका टेबलचा विचार करा.

कार्य	अनेक मूल्ये
y = kx + b	E(y) = (-∞;+∞)
y=x2n	E(y) =
y = cos x	E(y) = [-1;1]
y = tg x	E(y) = (-∞;+∞)
y = ctg x	E(y) = (-∞;+∞)
y = arcsin x	E(y) = [-π/2 ; π/2]
y = arcos x	E(y) =
y = आर्कटान x	E(y) = (-π/2; π/2)
y = arcctg x	E(y) = (0; π)

हे देखील लक्षात घ्या की सम डिग्रीच्या कोणत्याही बहुपदीची श्रेणी मध्यांतर आहे, जिथे n हे या बहुपदीचे सर्वात मोठे मूल्य आहे.

II. फंक्शनची श्रेणी शोधण्यासाठी वापरलेले फंक्शन गुणधर्म

फंक्शनच्या मूल्यांचा संच यशस्वीरित्या शोधण्यासाठी, एखाद्याला मूलभूत प्राथमिक फंक्शन्सच्या गुणधर्मांचे चांगले ज्ञान असणे आवश्यक आहे, विशेषत: त्यांचे परिभाषाचे डोमेन, मूल्यांच्या श्रेणी आणि मोनोटोनिसिटीचे स्वरूप. आपण सतत, मोनोटोन डिफरेंशिएबल फंक्शन्सचे गुणधर्म सादर करूया, जे बहुतेक वेळा फंक्शन्सच्या व्हॅल्यूजचा सेट शोधण्यासाठी वापरले जातात.

गुणधर्म 2 आणि 3 सामान्यतः प्राथमिक कार्याच्या गुणधर्मासह त्याच्या डोमेनमध्ये सतत वापरल्या जातात. या प्रकरणात, फंक्शनच्या मूल्यांचा संच शोधण्याच्या समस्येचा सर्वात सोपा आणि सर्वात लहान उपाय गुणधर्म 1 च्या आधारे प्राप्त केला जातो, जर सोप्या पद्धतींचा वापर करून फंक्शनची मोनोटोनिसिटी निर्धारित करणे शक्य असेल. फंक्शन, व्यतिरिक्त, सम किंवा विषम, नियतकालिक इ. असल्यास समस्येचे निराकरण आणखी सोपे केले जाते. अशा प्रकारे, फंक्शन व्हॅल्यूजचे संच शोधण्याच्या समस्या सोडवताना, फंक्शनचे खालील गुणधर्म तपासले पाहिजेत आणि आवश्यकतेनुसार वापरले पाहिजेत:

• सातत्य
• मोनोटोन;
• भिन्नता;
• सम, विषम, नियतकालिक इ.

फंक्शन व्हॅल्यूचा संच शोधण्यासाठी सोपी कार्ये मुख्यतः अभिमुख असतात:

अ) सर्वात सोप्या अंदाज आणि निर्बंधांचा वापर: (2 x > 0, -1 ≤ sinx? 1, 0 ≤ cos 2 x? 1, इ.);

b) पूर्ण वर्ग निवडण्यासाठी: x 2 - 4x + 7 \u003d (x - 2) 2 + 3;

c) त्रिकोणमितीय अभिव्यक्तींच्या परिवर्तनासाठी: 2sin 2 x - 3cos 2 x + 4 = 5sin 2 x +1;

d) फंक्शनची मोनोटोनिसिटी x 1/3 + 2 x-1 वापरून R ने वाढते.

III. फंक्शन्सच्या श्रेणी शोधण्याचे मार्ग विचारात घ्या.

अ) जटिल फंक्शन वितर्कांच्या मूल्यांचा अनुक्रमिक शोध;
ब) मूल्यांकन पद्धत;
c) फंक्शनची सातत्य आणि मोनोटोनिसिटीचे गुणधर्म वापरणे;
ड) डेरिव्हेटिव्हचा वापर;
e) फंक्शनच्या सर्वात मोठ्या आणि सर्वात लहान मूल्यांचा वापर;
f) ग्राफिकल पद्धत;
g) पॅरामीटर परिचय पद्धत;
h) व्यस्त कार्य पद्धत.

आम्ही विशिष्ट उदाहरणांवर या पद्धतींचे सार प्रकट करू.

उदाहरण 1: श्रेणी शोधा E(y)फंक्शन्स y = लॉग 0.5 (4 - 2 3 x - 9 x).

जटिल फंक्शन आर्ग्युमेंट्सची मूल्ये क्रमशः शोधून हे उदाहरण सोडवू. लॉगरिदम अंतर्गत पूर्ण चौरस निवडल्यानंतर, आम्ही फंक्शनचे रूपांतर करतो

y = लॉग 0.5 (5 - (1 + 2 3 x - 3 2x)) = लॉग 0.5 (5 - (3 x + 1) 2)

आणि क्रमशः त्याच्या जटिल वितर्कांच्या मूल्यांचे संच शोधा:

E(3 x) = (0;+∞), E(3 x + 1) = (1;+∞), E(-(3 x + 1) 2 = (-∞;-1), E(5 – (3 x +1) 2) = (-∞;4)

सूचित करा ट= 5 – (3 x +1) 2 , जेथे -∞≤ t≤4. अशाप्रकारे, किरणांवर y = log 0.5 t फंक्शनच्या मूल्यांचा संच शोधण्यात समस्या कमी होते. (-∞;4) . फंक्शन y = log 0.5 t फक्त येथे परिभाषित केले असल्याने, किरण (-∞;4) वरील त्याच्या मूल्यांचा संच मध्यांतर (0;4) वरील फंक्शनच्या मूल्यांच्या संचाशी एकरूप होतो, जे लॉगरिदमिक फंक्शनच्या परिभाषा (0;+∞) डोमेनसह किरण (-∞;4) चे छेदनबिंदू आहे. मध्यांतरावर (0;4) हे कार्य सतत आणि कमी होत आहे. येथे ट> 0, ते +∞ कडे झुकते आणि कधी t = 4 हे मूल्य -2 घेते, म्हणून E(y) =(-2, +∞).

उदाहरण 2: फंक्शनची श्रेणी शोधा

y = cos7x + 5cosx

आपण हे उदाहरण अंदाजाच्या पद्धतीद्वारे सोडवू या, ज्याचा सार खालील आणि वरून सतत कार्याचा अंदाज लावणे आणि कार्य अंदाजांच्या खालच्या आणि वरच्या सीमांपर्यंत पोहोचते हे सिद्ध करण्यासाठी आहे. या प्रकरणात, अंदाजाच्या खालच्या सीमारेषेपासून वरच्या एकापर्यंतच्या मध्यांतरासह फंक्शनच्या मूल्यांच्या संचाचा योगायोग फंक्शनच्या सातत्य आणि त्यासाठी इतर मूल्यांच्या अनुपस्थितीद्वारे निर्धारित केला जातो.

असमानता -1≤cos7x?1, -5≤5cosx?5 वरून आम्हाला -6≤y?6 अंदाज येतो. x = p आणि x = 0 साठी, फंक्शन -6 आणि 6 मूल्ये घेते, म्हणजे. खालच्या आणि वरच्या सीमांवर पोहोचते. सतत फंक्शन्स cos7x आणि cosx चे रेखीय संयोजन म्हणून, फंक्शन y संपूर्ण संख्या अक्षावर सतत असते, म्हणून, सतत फंक्शनच्या गुणधर्मानुसार, ते -6 ते 6 पर्यंत सर्व मूल्ये घेते, आणि फक्त त्यांना, पासून , असमानता -6≤y?6, इतर मूल्यांमुळे ती अशक्य आहे. परिणामी, E(y)= [-6;6].

उदाहरण 3: श्रेणी शोधा E(f)कार्ये f(x)= cos2x + 2cosx.

दुहेरी कोन कोसाइन सूत्र वापरून, आपण फंक्शनचे रूपांतर करतो f(x)= 2cos 2 x + 2cosx – 1 आणि दर्शवा ट= cosx. मग f(x)= 2t 2 + 2t – 1. पासून E(cosx) =

[-1;1], नंतर फंक्शनची श्रेणी f(x)फंक्शन g च्या मूल्यांच्या संचाशी एकरूप आहे (ट)\u003d 2t 2 + 2t - 1 विभागावर [-1; 1], जे आपण ग्राफिकल पद्धतीने शोधू. मध्यांतर [-1; 1] वर y = 2t 2 + 2t - 1 = 2(t + 0.5) 2 - 1.5 फंक्शन प्लॉट केल्यावर, आम्हाला आढळते E(f) = [-1,5; 3].

टीप - पॅरामीटरच्या अनेक समस्या फंक्शनच्या मूल्यांचा संच शोधण्यात कमी केल्या जातात, मुख्यतः सोडविण्यायोग्यता आणि समीकरण आणि असमानतेच्या समाधानांच्या संख्येशी संबंधित. उदाहरणार्थ, समीकरण f(x)= a जर आणि फक्त तरच सोडवता येण्याजोगा आहे

aE(f)असेच समीकरण f(x)= a मध्ये काही अंतराल X वर कमीत कमी एक रूट आहे, किंवा या मध्यांतरावर कोणतेही रूट नाही जर आणि फक्त फंक्शनच्या मूल्यांच्या संचाशी संबंधित असेल किंवा नसेल तर f(x)अंतराल X वर. आम्ही फंक्शनच्या मूल्यांचा संच आणि असमानता वापरून देखील अभ्यास करतो f(x)≠एक f(x)>एक इ. विशेषतः, f(x)≠आणि x च्या सर्व स्वीकार्य मूल्यांसाठी, जर एक E(f)

उदाहरण 4. पॅरामीटर a च्या कोणत्या मूल्यांसाठी, समीकरण (x + 5) 1/2 = a (x 2 + 4) खंडावर एकच मूळ आहे [-4;-1].

चला समीकरण (x + 5) 1/2 / (x 2 + 4) = a या स्वरूपात लिहू. शेवटच्या समीकरणामध्ये सेगमेंटवर किमान एक रूट आहे [-4;-1] जर आणि फक्त जर ए फंक्शनच्या मूल्यांच्या संचाशी संबंधित असेल तर f(x) =(x + 5) 1/2 / (x 2 + 4) विभागावर [-4;-1]. फंक्शनच्या सातत्य आणि मोनोटोनिसिटीचा गुणधर्म वापरून हा संच शोधू.

खंड [-4;-1] वर फंक्शन y = xІ + 4 हे सतत, कमी होत जाणारे आणि धनात्मक असते, म्हणून फंक्शन g(x) = 1/(x 2 + 4) सतत आहे आणि या मध्यांतराने वाढते, कारण जेव्हा सकारात्मक कार्याने विभाजित केले जाते, तेव्हा फंक्शनच्या मोनोटोनिसिटीचे स्वरूप उलट बदलते. कार्य h(x) =(x + 5) 1/2 त्याच्या डोमेनमध्ये सतत आणि वाढत आहे D(h) =[-5;+∞) आणि, विशेषतः, मध्यांतर [-4;-1] वर, जेथे ते देखील सकारात्मक आहे. मग फंक्शन f(x)=g(x) h(x), दोन सतत, वाढत्या आणि सकारात्मक कार्यांचे उत्पादन म्हणून, ते देखील सतत असते आणि सेगमेंट [-4;-1] वर वाढते, म्हणून त्याच्या [-4;-1] वरील मूल्यांचा संच हा विभाग आहे [-4;-1] f(-4); f(-1)] = म्हणून, समीकरणाचे मध्यांतर [-4;-1] वर समाधान आहे, आणि 0.05 ≤ a ≤ 0.4 साठी फक्त एक (सतत मोनोटोन फंक्शनच्या गुणधर्मानुसार).

टिप्पणी. समीकरणाची निराकरणक्षमता f(x) = aकाही अंतरावर X हे पॅरामीटरच्या मूल्यांच्या समतुल्य आहे aकार्य मूल्यांचा संच f(x) X वर. म्हणून, फंक्शनच्या मूल्यांचा संच f(x)मध्यांतरावर X पॅरामीटर मूल्यांच्या संचाशी एकरूप होतो a, ज्यासाठी समीकरण f(x) = aअंतराल X वर किमान एक रूट आहे. विशेषतः, मूल्यांची श्रेणी E(f)कार्ये f(x)पॅरामीटर मूल्यांच्या संचाशी जुळते a, ज्यासाठी समीकरण f(x) = aकिमान एक रूट आहे.

उदाहरण 5: श्रेणी शोधा E(f)कार्ये

एक पॅरामीटर सादर करून उदाहरण सोडवू या, त्यानुसार E(f)पॅरामीटर मूल्यांच्या संचाशी जुळते a, ज्यासाठी समीकरण

किमान एक रूट आहे.

जेव्हा a=2, समीकरण रेखीय असते - 4x - 5 = 0 अज्ञात x साठी शून्य नसलेल्या गुणांकासह, म्हणून त्याला एक उपाय आहे. a≠2 साठी, समीकरण चतुर्भुज आहे, म्हणून ते सोडवता येण्याजोगे आहे जर आणि फक्त त्याचा भेदभाव असेल तर

बिंदू a = 2 विभागातील असल्याने

नंतर पॅरामीटर मूल्यांचा इच्छित संच एकम्हणून मूल्यांची श्रेणी E(f)संपूर्ण विभाग असेल.

फंक्शनच्या व्हॅल्यूजचा संच शोधताना पॅरामीटर सादर करण्याच्या पद्धतीचा थेट विकास म्हणून, x साठी समीकरण सोडवण्यासाठी कोणते आवश्यक आहे हे शोधण्यासाठी आपण व्यस्त फंक्शनच्या पद्धतीचा विचार करू शकतो. f(x)=y, पॅरामीटर म्हणून y विचारात घ्या. जर या समीकरणाला एक अनोखा उपाय असेल x=g(y), नंतर श्रेणी E(f)मूळ कार्य f(x)व्याख्येच्या डोमेनशी जुळते D(g)व्यस्त कार्य g(y). जर समीकरण f(x)=yअनेक उपाय आहेत x = g 1 (y), x \u003d g 2 (y)इत्यादी, नंतर E(f)फंक्शन व्याख्यांच्या व्याप्तीच्या युनियनच्या समान आहे g 1 (y), g 2 (y)इ.

उदाहरण 6: श्रेणी शोधा E(y)फंक्शन्स y = 5 2/(1-3x).

समीकरणातून

व्यस्त कार्य x = लॉग 3 (लॉग 5 y – 2)/(लॉग 5 y)) आणि त्याचे डोमेन शोधा D(x):

कारण x साठी समीकरण एक अद्वितीय समाधान आहे

E(y) = D(x) = (0; 1)(25;+∞ )

जर एखाद्या फंक्शनच्या डोमेनमध्ये अनेक इंटरव्हल्स असतील किंवा वेगवेगळ्या इंटरव्हलवरील फंक्शन वेगवेगळ्या सूत्रांद्वारे दिलेले असेल, तर फंक्शनचे डोमेन शोधण्यासाठी, तुम्हाला प्रत्येक इंटरव्हलवर फंक्शनच्या व्हॅल्यूजचे संच शोधून त्यांचे घेणे आवश्यक आहे. संघ

उदाहरण 7: श्रेणी शोधा f(x)आणि f(f(x)), कुठे

f(x)किरण (-∞;1] वर, जेथे ते 4 x + 9 4 -x + 3 या अभिव्यक्तीशी एकरूप होते. t = 4 x. मग f(x) = t + 9/t + 3, जेथे 0< t ≤ 4 , так как показательная функция непрерывно возрастает на луче (-∞;1] и стремится к нулю при х → -∞. Тем самым множество значений функции f(x)किरणांवर (-∞;1] फंक्शनच्या मूल्यांच्या संचाशी एकरूप होतो g(t) = t + 9/t + 3, मध्यांतरावर (0;4], जे आपण व्युत्पन्न वापरून शोधतो g'(t) \u003d 1 - 9 / t 2. मध्यांतरावर (0;4] व्युत्पन्न g'(t)येथे परिभाषित केले आहे आणि तेथे अदृश्य होते t=3. 0 वाजता<ट<3 она отрицательна, а при 3<ट<4 положительна. Следовательно, в интервале (0;3) функция g(t)कमी होते, आणि मध्यांतरात (3;4) ते वाढते, संपूर्ण मध्यांतर (0;4) वर सतत राहते, त्यामुळे g (3)= 9 - मध्यांतरावरील या फंक्शनचे सर्वात लहान मूल्य (0; 4], त्याचे सर्वात मोठे मूल्य अस्तित्वात नसताना, तेव्हा t→0योग्य कार्य g(t)→+∞.त्यानंतर, सतत फंक्शनच्या गुणधर्माद्वारे, फंक्शनच्या मूल्यांचा संच g(t)मध्यांतरावर (0;4], आणि म्हणून मूल्यांचा संच f(x)(-∞;-1] वर, एक किरण असेल.

आता, अंतराल एकत्र करून - फंक्शन व्हॅल्यूजचे संच f(f(x)), सूचित करा t = f(x). मग f(f(x)) = f(t), कुठे टकार्य f(t)= 2cos( x-1) 1/2+ 7 आणि ते पुन्हा 5 ते 9 पर्यंत सर्व मूल्ये घेते, उदा. श्रेणी E(fІ) = E(f(f(x))) =.

त्याचप्रमाणे, सूचित करणे z = f(f(x)), आपण श्रेणी शोधू शकता E(f3)कार्ये f(f(f(x))) = f(z), जेथे 5 ≤ z ≤ 9, इ. याची खात्री करा E(f 3) = .

फंक्शन व्हॅल्यूजचा संच शोधण्याची सर्वात सार्वत्रिक पद्धत म्हणजे दिलेल्या अंतराने फंक्शनची सर्वात मोठी आणि सर्वात लहान व्हॅल्यू वापरणे.

उदाहरण 8. पॅरामीटरच्या कोणत्या मूल्यांसाठी आरअसमानता 8 x - p ≠ 2x+1 – 2xसर्वांसाठी धरून ठेवते -1 ≤ x< 2.

सूचित करणे t = 2 x, आम्ही असमानता म्हणून लिहितो p ≠ t 3 - 2t 2 + t. कारण t = 2 xवर सतत वाढणारे कार्य आहे आर,नंतर -1 ≤ x साठी< 2 переменная

2 -1 ≤ टी<2 2 ↔

0.5 ≤ टी< 4, и исходное неравенство выполняется для всех -1 ≤ x < 2 тогда и только тогда, когда आरकार्य मूल्यांपेक्षा भिन्न f(t) \u003d t 3 - 2t 2 + t 0.5 ≤ t वर< 4.

प्रथम फंक्शनच्या व्हॅल्यूजचा संच शोधू f(t)मध्यांतरावर जेथे त्याचे सर्वत्र व्युत्पन्न आहे f'(t) = 3t 2 - 4t + 1. परिणामी, f(t)वेगळे करण्यायोग्य आहे, आणि म्हणून सेगमेंटवर सतत आहे. समीकरणातून f'(t) = 0फंक्शनचे महत्त्वपूर्ण मुद्दे शोधा t=1/3, t=1,त्यापैकी पहिला विभागाचा नाही आणि दुसरा त्याचा आहे. कारण f(0.5) = 1/8, f(1) = 0, f(4) = 36,नंतर, भिन्नता असलेल्या फंक्शनच्या गुणधर्मानुसार, 0 हे सर्वात लहान आहे आणि 36 हे फंक्शनचे सर्वात मोठे मूल्य आहे f(t)विभागावर. मग f(t),सतत फंक्शन म्हणून, 0 ते 36 पर्यंतची सर्व मूल्ये सेगमेंटवर घेते, आणि मूल्य 36 तेव्हाच घेते जेव्हा t=4, म्हणून 0.5 ≤ t साठी< 4, она принимает все значения из промежутка . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

चला एक समस्या घेऊ ज्यामध्ये आर्कसिनच्या मूल्यांची श्रेणी निश्चित करणे आवश्यक आहे.

उदाहरण १

परिस्थिती:श्रेणी y = a r c sin x शोधा.

उपाय

सर्वसाधारण बाबतीत, आर्कसिनच्या व्याख्येचे क्षेत्र मध्यांतरावर स्थित आहे [ - 1 ; एक] आपल्याला त्यावरील निर्दिष्ट फंक्शनचे सर्वात मोठे आणि सर्वात लहान मूल्य निर्धारित करणे आवश्यक आहे.

y "= a r c sin x" = 1 1 - x 2

आम्हाला माहित आहे की फंक्शनचे व्युत्पन्न मध्यांतर [ - 1 ; 1 ] , म्हणजे, संपूर्ण व्याख्येच्या क्षेत्रामध्ये, आर्कसिन फंक्शन वाढेल. याचा अर्थ x जेव्हा - 1 असेल तेव्हा ते सर्वात लहान मूल्य घेईल आणि सर्वात मोठे - जेव्हा x 1 च्या बरोबरीचे असेल.

m i n x ∈ - 1 ; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2

अशा प्रकारे, आर्कसिन फंक्शनची श्रेणी E (a r c sin x) = - π 2 ; π 2

उत्तर: E (a r c sin x) \u003d - π 2; π २

उदाहरण २

परिस्थिती:दिलेल्या मध्यांतरावर y = x 4 - 5 x 3 + 6 x 2 श्रेणीची गणना करा [ 1 ; चार]

उपाय

दिलेल्या अंतरालमधील फंक्शनच्या सर्वात मोठ्या आणि सर्वात लहान मूल्याची गणना करायची आहे.

टोकाचे बिंदू निश्चित करण्यासाठी, खालील गणना करणे आवश्यक आहे:

y "= x 4 - 5 x 3 + 6 x 2" = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 आणि l आणि 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1;4 ;x3 = 15 + 338 ≈ 2.59 ∈ 1;4

आता सेगमेंटच्या शेवटी दिलेल्या फंक्शनची व्हॅल्यू शोधू आणि बिंदू x 2 = 15 - 33 8 ; x ३ \u003d १५ + ३३ ८:

y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 2 08 y 15 + 33 8 = 15 + 33 8 4 - 5 15 + 33 8 3 + 6 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 y (4) = 4 4 - 5 4 3 + 6 4 2 = 32

याचा अर्थ असा की फंक्शन व्हॅल्यूजचा संच 117 - 165 33 512 या विभागाद्वारे निर्धारित केला जाईल; ३२ .

उत्तर: 117 - 165 33 512 ; 32 .

अंतराल (a ; b) , आणि a मधील सतत फंक्शन y = f (x) च्या मूल्यांचा संच शोधण्यासाठी पुढे जाऊया; + ∞ , - ∞ ; b , -∞ ; +∞

सर्वात मोठे आणि सर्वात लहान बिंदू तसेच दिलेल्या मध्यांतरातील वाढ आणि घट यांचे मध्यांतर ठरवून सुरुवात करूया. त्यानंतर, आम्हाला मध्यांतराच्या शेवटी एकतर्फी मर्यादा आणि/किंवा अनंत मर्यादा मोजण्याची आवश्यकता असेल. दुसऱ्या शब्दांत, दिलेल्या परिस्थितीनुसार फंक्शनचे वर्तन निश्चित करणे आवश्यक आहे. यासाठी आमच्याकडे सर्व आवश्यक डेटा आहे.

उदाहरण ३

परिस्थिती:मध्यांतर (- 2 ; 2) वर फंक्शन y = 1 x 2 - 4 च्या श्रेणीची गणना करा.

उपाय

दिलेल्या अंतरावर फंक्शनचे सर्वात मोठे आणि सर्वात लहान मूल्य निश्चित करा

y "= 1 x 2 - 4" = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2; 2)

आम्हाला 0 च्या बरोबरीचे कमाल मूल्य मिळाले, कारण या टप्प्यावर फंक्शनचे चिन्ह बदलते आणि आलेख कमी होऊ लागतो. चित्र पहा:

म्हणजेच, y (0) = 1 0 2 - 4 = - 1 4 हे फंक्शनचे कमाल मूल्य असेल.

आता x साठी फंक्शनचे वर्तन परिभाषित करूया ज्याचा कल - 2 उजवीकडे आणि + 2 डावीकडे आहे. दुसऱ्या शब्दांत, आम्हाला एकतर्फी मर्यादा आढळतात:

लिम x → - 2 + 0 1 x 2 - 4 = लिम x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 1 + 0 = - ∞ लिम x → 2 + 0 1 x 2 - 4 = लिम x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = -∞

आम्हाला समजले की फंक्शन व्हॅल्यूज वजा अनंत वरून - 1 4 पर्यंत वाढतील जेव्हा वितर्क - 2 वरून 0 मध्ये बदलेल. आणि जेव्हा वितर्क 0 ते 2 पर्यंत बदलते तेव्हा फंक्शनची मूल्ये वजा अनंताकडे कमी होतात. म्हणून, दिलेल्या फंक्शनच्या व्हॅल्यूजचा संच आपल्याला आवश्यक असलेल्या मध्यांतरावर असेल (- ∞ ; - 1 4 ] .

उत्तर: (- ∞ ; - 1 4 ] .

उदाहरण ४

परिस्थिती: दिलेल्या मध्यांतरावर y = t g x मूल्यांचा संच दर्शवा - π 2 ; π 2

उपाय

आम्हाला माहित आहे की, सर्वसाधारणपणे, स्पर्शिकेचे व्युत्पन्न - π 2; π 2 सकारात्मक असेल, म्हणजेच कार्य वाढेल. आता दिलेल्या सीमांमध्ये फंक्शन कसे वागते ते परिभाषित करूया:

लिम x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ लिम x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

जेव्हा युक्तिवाद - π 2 वरून π 2 पर्यंत बदलतो तेव्हा आम्ही फंक्शनच्या मूल्यांमध्ये वजा अनंत ते प्लस अनंतापर्यंत वाढ प्राप्त केली आहे आणि आम्ही असे म्हणू शकतो की या फंक्शनच्या समाधानाचा संच सर्व वास्तविकतेचा संच असेल. संख्या

उत्तर: - ∞ ; + ∞ .

उदाहरण 5

परिस्थिती:नैसर्गिक लॉगरिथम फंक्शन y = ln x ची श्रेणी काय आहे हे निर्धारित करा.

उपाय

आम्हाला माहित आहे की हे कार्य वितर्क D (y) = 0 च्या सकारात्मक मूल्यांसाठी परिभाषित केले आहे; +∞ दिलेल्या मध्यांतरावरील व्युत्पन्न धनात्मक असेल: y " = ln x " = 1 x . याचा अर्थ त्यावर फंक्शन वाढत आहे. पुढे, जेव्हा युक्तिवाद 0 (उजवीकडे) वर जातो आणि जेव्हा x अनंताकडे जातो तेव्हा केससाठी एक-बाजूची मर्यादा परिभाषित करणे आवश्यक आहे:

लिम x → 0 + 0 ln x = ln (0 + 0) = - ∞ लिम x → ∞ ln x = ln + ∞ = + ∞

आम्हाला आढळले आहे की फंक्शनची मूल्ये वजा अनंतापासून प्लस अनंतापर्यंत वाढतील कारण x मूल्ये शून्य ते प्लस अनंतात बदलतात. याचा अर्थ असा की सर्व वास्तविक संख्यांचा संच नैसर्गिक लॉगरिथम कार्याची श्रेणी आहे.

उत्तर:सर्व वास्तविक संख्यांचा संच नैसर्गिक लॉगरिथम कार्याची श्रेणी आहे.

उदाहरण 6

परिस्थिती: y = 9 x 2 + 1 फंक्शनची श्रेणी काय आहे ते ठरवा.

उपाय

हे फंक्शन परिभाषित केले आहे जर x ही वास्तविक संख्या असेल. चला फंक्शनची सर्वात मोठी आणि सर्वात लहान मूल्ये तसेच त्याच्या वाढ आणि घटाच्या मध्यांतरांची गणना करूया:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

परिणामी, आम्ही निर्धारित केले आहे की हे कार्य कमी होईल जर x ≥ 0; x ≤ 0 असल्यास वाढवा; जेव्हा व्हेरिएबल 0 असेल तेव्हा त्याचा कमाल बिंदू y (0) = 9 0 2 + 1 = 9 असतो.

फंक्शन अनंतात कसे वागते ते पाहू:

लिम x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 लिम x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = +0

रेकॉर्डवरून असे दिसून येते की या प्रकरणात फंक्शनची मूल्ये अस्पष्टपणे 0 पर्यंत पोहोचतील.

थोडक्यात: जेव्हा वितर्क वजा अनंतापासून शून्यावर बदलतो, तेव्हा फंक्शनची मूल्ये 0 ते 9 पर्यंत वाढतात. आर्ग्युमेंट व्हॅल्यूज 0 ते प्लस इन्फिनिटीवर जाताना, संबंधित फंक्शन व्हॅल्यू 9 ते 0 पर्यंत कमी होतील. आम्ही आकृतीमध्ये हे चित्रित केले आहे:

हे दर्शविते की फंक्शनची श्रेणी मध्यांतर E (y) = (0 ; 9 ] असेल.

उत्तर: E (y) = (0 ; 9 ]

जर आपल्याला मध्यांतरांवर y = f (x) फंक्शनच्या मूल्यांचा संच निश्चित करायचा असेल तर [ a ; b) , (a ; b ] , [ a ; + ∞ ) , (- ∞ ; b ] , नंतर आपल्याला तंतोतंत समान अभ्यास करणे आवश्यक आहे. आम्ही अद्याप या प्रकरणांचे विश्लेषण करणार नाही: आम्ही त्यांना नंतर समस्यांमध्ये भेटू. .

परंतु एखाद्या विशिष्ट फंक्शनचे डोमेन अनेक अंतरालांचे एकत्रीकरण असल्यास काय? मग आपल्याला या प्रत्येक मध्यांतरावरील मूल्यांचे संच मोजावे लागतील आणि ते एकत्र करावे लागतील.

उदाहरण 7

परिस्थिती: y = x x - 2 ची श्रेणी काय असेल ते ठरवा.

उपाय

कारण फंक्शनचा भाजक 0 मध्ये बदलू नये, तर D (y) = - ∞ ; २ ∪ २ ; +∞

पहिल्या सेगमेंटवर फंक्शन व्हॅल्यूजचा सेट परिभाषित करून सुरुवात करूया - ∞ ; 2, जे एक ओपन बीम आहे. आपल्याला माहित आहे की त्यावरील फंक्शन कमी होईल, म्हणजेच या फंक्शनचे व्युत्पन्न नकारात्मक असेल.

लिम x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ लिम x → - ∞ x x - 2 = लिम x → - ∞ x - 2 + 2 x - 2 = लिम x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

मग, ज्या प्रकरणांमध्ये युक्तिवाद वजा अनंताकडे बदलतो, फंक्शनची मूल्ये अस्पष्टपणे 1 कडे जातील. जर x ची मूल्ये उणे अनंत वरून 2 वर बदलली, तर मूल्ये 1 वरून अनंतापर्यंत कमी होतील, म्हणजे. या विभागावरील फंक्शन मध्यांतर पासून मूल्ये घेईल - ∞ ; एक आम्ही आमच्या तर्कातून ऐक्य वगळतो, कारण फंक्शनची मूल्ये त्याच्यापर्यंत पोहोचत नाहीत, परंतु केवळ अस्पष्टपणे त्याच्याकडे जातात.

ओपन बीम 2 साठी; + ∞ आम्ही अगदी त्याच क्रिया करतो. त्यावरील कार्य देखील कमी होत आहे:

लिम x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ लिम x → + ∞ x x - 2 = लिम x → + ∞ x - 2 + 2 x - 2 = लिम x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

या विभागावरील फंक्शनची मूल्ये सेट 1 द्वारे निर्धारित केली जातात; +∞ याचा अर्थ आपल्याला आवश्यक असलेल्या स्थितीत निर्दिष्ट केलेल्या फंक्शनच्या मूल्यांची श्रेणी संचांची युनियन असेल - ∞; 1 आणि 1; +∞

उत्तर: E (y) = - ∞ ; 1 ∪ 1; +∞

हे चार्टवर पाहिले जाऊ शकते:

एक विशेष बाब म्हणजे नियतकालिक कार्ये. त्यांचे मूल्य क्षेत्र या कार्याच्या कालावधीशी संबंधित असलेल्या मध्यांतरावरील मूल्यांच्या संचाशी जुळते.

उदाहरण 8

परिस्थिती: sine y = sin x ची श्रेणी निश्चित करा.

उपाय

साइन हे नियतकालिक कार्याचा संदर्भ देते आणि त्याचा कालावधी 2 pi आहे. आम्ही सेगमेंट 0 घेतो; 2 π आणि त्यावरील मूल्यांचा संच काय असेल ते पहा.

y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

0 च्या आत; 2 π फंक्शनमध्ये अत्यंत बिंदू असतील π 2 आणि x = 3 π 2. त्यामध्ये फंक्शनची व्हॅल्यू काय समान असतील, तसेच सेगमेंटच्या सीमारेषेवर आपण गणना करू या, त्यानंतर आपण सर्वात मोठे आणि सर्वात लहान मूल्य निवडू.

y (0) = पाप 0 = 0 y π 2 = पाप π 2 = 1 y 3 π 2 = पाप 3 π 2 = - 1 y (2 π) = पाप (2 π) = 0 ⇔ मिनिट x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1 , कमाल x ∈ 0 ; 2 π sinx \u003d sin π 2 \u003d 1

उत्तर: E (sinx) = - 1 ; एक

तुम्हाला घातांक, घातांक, लॉगरिदमिक, त्रिकोणमितीय, व्यस्त त्रिकोणमिती यासारख्या कार्यांच्या श्रेणी जाणून घ्यायच्या असल्यास, आम्ही तुम्हाला मूलभूत प्राथमिक कार्यांवरील लेख पुन्हा वाचण्याचा सल्ला देतो. आम्ही येथे सादर केलेला सिद्धांत आम्हाला तेथे निर्दिष्ट केलेल्या मूल्यांची चाचणी घेण्यास अनुमती देतो. ते शिकणे इष्ट आहे, कारण समस्या सोडवण्यासाठी त्यांची आवश्यकता असते. जर तुम्हाला मुख्य फंक्शन्सच्या रेंज माहित असतील, तर तुम्ही भौमितिक ट्रान्सफॉर्मेशन वापरून प्राथमिक फंक्शन्समधून मिळवलेल्या फंक्शन्सच्या रेंज सहज शोधू शकता.

उदाहरण ९

परिस्थिती:श्रेणी निश्चित करा y = 3 a r c cos x 3 + 5 π 7 - 4 .

उपाय

आपल्याला माहित आहे की 0 ते pi खंड ही व्यस्त कोसाइनची श्रेणी आहे. दुसऱ्या शब्दांत, E (a r c cos x) = 0 ; π किंवा 0 ≤ a r c cos x ≤ π . आपण चाप कोसाइनमधून a r c cos x 3 + 5 π 7 फंक्शन O x अक्षाच्या बाजूने हलवून आणि ताणून मिळवू शकतो, परंतु अशा परिवर्तनांमुळे आपल्याला काहीही मिळणार नाही. म्हणून, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π.

फंक्शन 3 a r c cos x 3 + 5 π 7 हे व्यस्त कोसाइन a r c cos x 3 + 5 π 7 मधून y-अक्षावर ताणून मिळवता येते, म्हणजे. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . अंतिम परिवर्तन हे O y अक्षाच्या बाजूने 4 मूल्यांनी केलेले एक शिफ्ट आहे. परिणामी, आम्हाला दुहेरी असमानता मिळते:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 अर्कोस x 3 + 5 π 7 - 4 ≤ 3 π - 4

आम्हाला समजले की आम्हाला आवश्यक असलेली श्रेणी E (y) = - 4 च्या बरोबरीची असेल; 3 pi - 4 .

उत्तर: E (y) = - 4 ; 3 pi - 4 .

स्पष्टीकरणाशिवाय आणखी एक उदाहरण लिहूया, कारण हे पूर्णपणे मागील सारखेच आहे.

उदाहरण 10

परिस्थिती: y = 2 2 x - 1 + 3 फंक्शनची श्रेणी काय असेल याची गणना करा.

उपाय

कंडिशनमध्ये दिलेले फंक्शन y = 2 · (2 ​​x - 1) - 1 2 + 3 असे पुन्हा लिहू. पॉवर फंक्शन y = x - 1 2 साठी अंतराल 0 वर श्रेणी परिभाषित केली जाईल; + ∞ , म्हणजे x - 1 2 > 0 . या प्रकरणात:

2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3

तर E (y) = 3 ; +∞

उत्तर: E (y) = 3 ; +∞

आता सतत नसलेल्या फंक्शनची रेंज कशी शोधायची ते पाहू. हे करण्यासाठी, आपल्याला संपूर्ण क्षेत्र मध्यांतरांमध्ये विभागणे आवश्यक आहे आणि त्या प्रत्येकावर मूल्यांचे संच शोधणे आवश्यक आहे आणि नंतर आपल्याकडे जे आहे ते एकत्र करणे आवश्यक आहे. हे अधिक चांगल्या प्रकारे समजून घेण्यासाठी, आम्ही तुम्हाला मुख्य प्रकारच्या फंक्शन ब्रेकपॉइंट्सचे पुनरावलोकन करण्याचा सल्ला देतो.

उदाहरण 11

परिस्थिती: y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3 फंक्शन दिले आहे< x ≤ 3 1 x - 3 , x >३ . त्याची श्रेणी मोजा.

उपाय

हे कार्य सर्व x मूल्यांसाठी परिभाषित केले आहे. 3 आणि 3 च्या बरोबरीच्या युक्तिवादाच्या मूल्यांसह सातत्य राखण्यासाठी त्याचे विश्लेषण करूया:

lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = लिम x → - 3 (1) = - 1 ⇒ लिम x → - 3 - 0 f (x) ≠ लिम x → - 3 + 0 f (x)

आमच्याकडे वितर्क - 3 च्या मूल्यासह पहिल्या प्रकारची एक अप्राप्य खंडितता आहे. जसजसे तुम्ही त्याच्याकडे जाल तसतसे फंक्शनची व्हॅल्यूज - 2 sin 3 2 - 4 कडे झुकतात आणि x उजवीकडे - 3 कडे झुकतात, व्हॅल्यू - 1 कडे झुकतात.

लिम x → 3 - 0 f(x) = लिम x → 3 - 0 (- 1) = 1 लिम x → 3 + 0 f(x) = लिम x → 3 + 0 1 x - 3 = + ∞

आमच्याकडे बिंदू 3 वर दुसर्‍या प्रकारची एक न काढता येणारी विसंगती आहे. जेव्हा फंक्शन त्याच्याकडे झुकते तेव्हा त्याची मूल्ये - 1 जवळ येतात, तर उजवीकडील त्याच बिंदूकडे - अनंततेकडे झुकतात.

याचा अर्थ असा की या फंक्शनच्या व्याख्येचे संपूर्ण क्षेत्र 3 अंतरांमध्ये विभागलेले आहे (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .

त्यापैकी पहिल्यावर, आम्हाला y \u003d 2 sin x 2 - 4 फंक्शन मिळाले. पासून - 1 ≤ sin x ≤ 1, आम्हाला मिळते:

1 ≤ पाप x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

याचा अर्थ या मध्यांतरावर (- ∞ ; - 3 ] फंक्शनच्या मूल्यांचा संच [ - 6 ; 2 ] आहे.

अर्ध-मांतरावर (- 3 ; 3 ] आपल्याला स्थिर फंक्शन y = - 1 मिळेल. परिणामी, या प्रकरणात त्याच्या मूल्यांचा संपूर्ण संच एक संख्या - 1 वर कमी होईल.

दुसऱ्या मध्यांतरावर 3 ; + ∞ आपल्याकडे y = 1 x - 3 फंक्शन आहे. ते कमी होत आहे कारण y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

लिम x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ लिम x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

म्हणून, x > 3 साठी मूळ फंक्शनच्या मूल्यांचा संच 0 आहे; +∞ आता परिणाम एकत्र करूया: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; +∞

उत्तर: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; +∞

उपाय आलेखामध्ये दर्शविले आहे:

उदाहरण 12

अट: एक फंक्शन आहे y = x 2 - 3 e x . त्याच्या मूल्यांचा संच निश्चित करा.

उपाय

हे सर्व वितर्क मूल्यांसाठी परिभाषित केले आहे जे वास्तविक संख्या आहेत. हे कार्य कोणत्या अंतराने वाढेल आणि कोणत्या मध्ये ते कमी होईल हे ठरवूया:

y "= x 2 - 3 e x" = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

आपल्याला माहित आहे की x = - 1 आणि x = 3 असल्यास व्युत्पन्न 0 होईल. आम्ही हे दोन बिंदू अक्षावर ठेवतो आणि परिणामी मध्यांतरांवर व्युत्पन्नाची कोणती चिन्हे असतील ते शोधतो.

फंक्शन (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) ने कमी होईल आणि [ - 1 ; 3]. किमान बिंदू असेल - 1 , कमाल - 3 .

आता संबंधित फंक्शन व्हॅल्यूज शोधूया:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

अनंतात फंक्शनचे वर्तन पाहू:

लिम x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ लिम x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = लिम x → + ∞ x 2 - 3 "e x" = लिम x → + ∞ 2 x e x = + ∞ + ∞ = = लिम x → + ∞ 2 x "(e x)" = 2 लिम x → + ∞ 1 e x = 2 1 + ∞ = + 0

दुसरी मर्यादा मोजण्यासाठी, L'Hopital चा नियम वापरला गेला. चला आपले समाधान आलेखावर प्लॉट करू.

हे दर्शविते की जेव्हा वितर्क मायनस इन्फिनिटी वरून - 1 वर बदलतो तेव्हा फंक्शनची मूल्ये प्लस अनंत वरून - 2 e पर्यंत कमी होतील. जर ते 3 ते अधिक अनंतात बदलले, तर मूल्ये 6 e - 3 वरून 0 पर्यंत कमी होतील, परंतु 0 पर्यंत पोहोचणार नाही.

अशा प्रकारे, E (y) = [ - 2 e ; +∞).

उत्तर: E (y) = [ - 2 e ; +∞)

तुम्हाला मजकुरात चूक आढळल्यास, कृपया ते हायलाइट करा आणि Ctrl+Enter दाबा